Lösungen quadratische Ungleichungen

a) –3x²+4x+5≥0

–3x²+4x+5=0 zugehörige Gleichung auf Null gestellt

D = 4²–4•(–3)•5

D = 16+60

D = 76

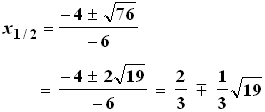Nullstellen ausrechnen

b) x²–3x+10 ≤ 0

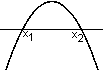
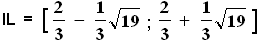
x²–3x+10 = 0

D = (–3)²–4•1• 10

D = 9 – 40

D = –31

Also keine Lösungen, das heißt: nach oben geöffnete Parabel oberhalb der x-Achse, bei der die y-Werte unterhalb oder auf (wegen „≤“) der x–Achse gesucht sind.

Es gibt solche Werte nicht:

L = { }

c) 2x²+98 > 28x

2x²–28x+98 > 0 alles auf eine Seite bringen

2x²–28x+98 = 0 die zugehörige quadratische Gleichung

D = (–28)²–4•2•98 Diskriminante aufstellen

D = 784–784

D = 0

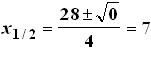
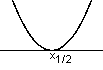
Nach oben geöffnete Parabel, die die x-Achse berührt.

Alle Werte außer der für x = 7 liegen über der x–Achse,

also L = R\{ 7 }