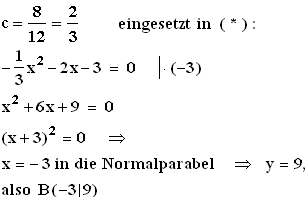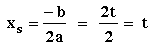
Lösungen Parabelscharen

Lösung zu 1:

y = (x – t)² + t (Scheitelform)

y = x² – 2tx + t² + t

Lösung zu 1 A:

Gegeben ist die Parabelschar y = x² – 2tx + t² + t.

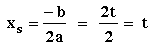
y_s = t² – 2t*t + t² + t = t

S_t(t / t)

Lösung zu 2 A:

Nullstellen:

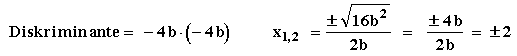
Scheitel:

x_s = 0

y_s = -4b

S(0/-4b)

Lösung zu 2 B:

Gemeinsame Punkte der Parabel und der Geraden g(y) = 2
bx² – 4b = 2
bx² – 4b – 2 = 0
Diskrimante = -4 * b * (-4b-2)
Berührpunkt bedeutet genau eine Nullstelle, also D=0, also
b = 0 oder -4b – 2 = 0, also
b = 0 oder b = -0,5

Lösung zu 2 C:

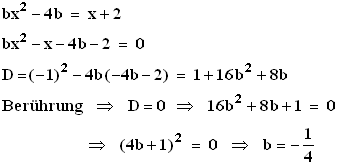
Lösung zu 3 A:

Scheitel auf Winkelhalbierende genau dann, wenn x_s = y_s, also: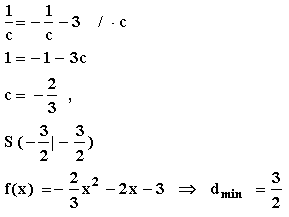

Lösung zu 3 B:

Gleichsetzen von f mit Normalparabel:

cx² - 2x – 3 = x²
(c – 1)x² – 2x – 3 = 0      ( * )

Genau ein Berührpunkt, wenn Diskriminante D = 0

D = B² - 4 AC = (-2)² - 4(c-1)*(-3)
= 4 + 12c – 12 = 0
12c =8