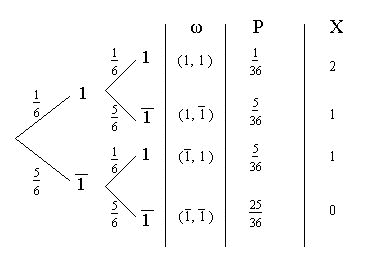
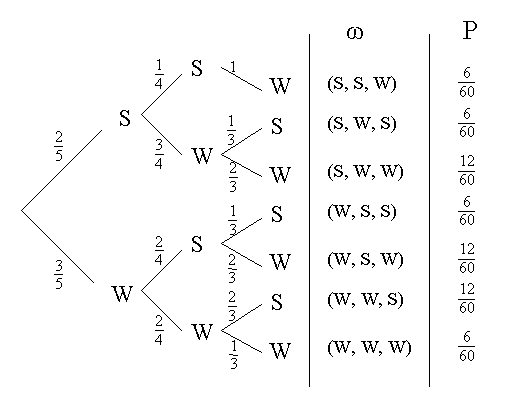
Baumdiagramm:

Wahrscheinlichkeitsverteilung:
x |
0 |
1 |
2 |
P(X=x) |
| Stabdiagramm: | Histogramm: |
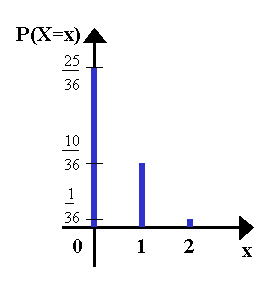 |
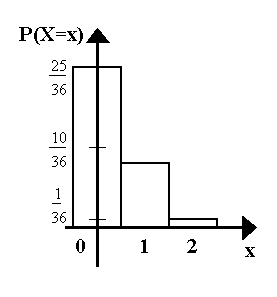 |
Baumdiagramm:
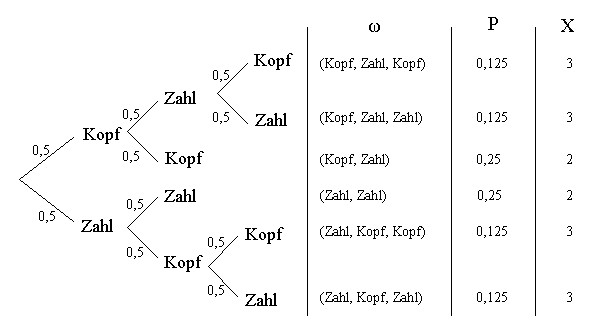
Wahrscheinlichkeitsverteilung:
x |
2 |
3 |
P(X=x) |
0,5 |
0,5 |
| Stabdiagramm: | Histogramm: |
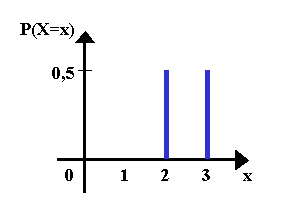 |
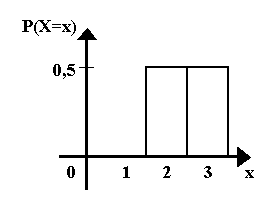 |
Firma A:
E(X) = 0 * 0,70 + 1 * 0,20 + 2 * 0,06 + 3 * 0,04 = 0,44
Var(X) = 02 * 0,70 + 12 * 0,20 + 22 * 0,06 + 32 * 0,04 - 0,442 = 0,61
![]()
Firma B:
E(X) = 0 * 0,76 + 1 * 0,04 + 2 * 0,20 + 3 * 0 = 0,44
Var(X) = 02 * 0,76 + 12 * 0,04 + 22 * 0,20 + 32 * 0 - 0,442 = 0,65
![]()
Die besseren Antriebsmotoren werden von Firma A hergestellt. Zwar ist der Erwartungswert bei beiden gleich, jedoch ist die Streuung um den Erwartungswert (Standardabweichung) bei Firma B höher.
x |
-2 |
0 |
2 |
P(X=x) |
|
Histogramm:
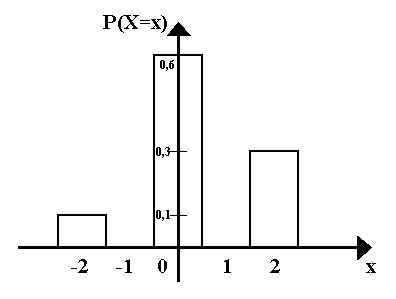
E(X) = (-2) * 0,1 + 0 * 0,6 + 2 * 0,3 = 0,4
Var(X) = (-2)2 * 0,1 + 02 * 0,6 + 22 * 0,3 - 0,42 = 1,44
![]()
ein faires Spiel herrscht, wenn E(X) = 0.
bisherige Auszahlung für schwarze Kugel: 2 €
neue Auszahlung: a
x |
-2 |
a - 2 |
2 a - 2 |
P(X=x) |
0,1 |
0,6 |
0,3 |
E(X) = -2 * 0,1 + (a - 2) * 0,6 + (2 a - 2) * 0,3 = 0
<=> -0,2 + 0,6a - 1,2 + 0,6a - 0,6 = 0
<=> -2 + 1,2a = 0
<=> a = 1,67
Um ein faires Spiel zu haben, muss für jede schwarze Kugel 1,67 € ausgezahlt werden.
Baumdiagramm:
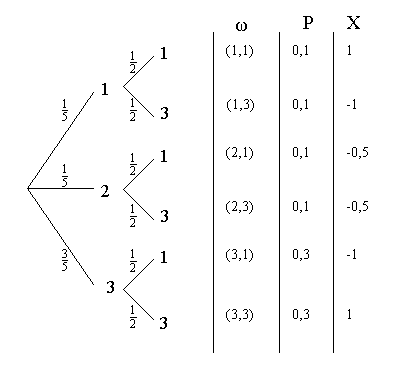
x |
- 1 |
- 0,5 |
1 |
P(X=x) |
0,4 |
0,2 |
0,4 |
Stabdiagramm:
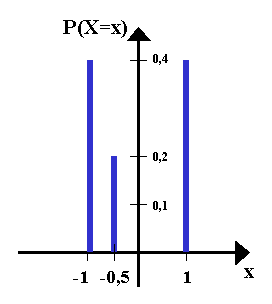
P(X < 0) = 0,4 + 0,2 = 0,6
E(X) = (-1) * 0,4 + (-0,5) * 0,2 + 1 * 0,4 = -0,1
Da der Erwartungswert ein Wert ungleich Null ist, handelt es sich um ein unfaires Spiel!
ein faires Spiel herrscht, wenn E(X) = 0.
bisherige Auszahlung für zwei gleiche Zahlen: 2 €
neue Auszahlung: a
x |
- 1 |
- 0,5 |
a -1 |
P(X=x) |
0,4 |
0,2 |
0,4 |
E(X) = (-1) * 0,4 + (-0,5) * 0,2 + (a-1) * 0,4 = 0
<=> -0,5 + 0,4a - 0,4 = 0
<=> -0,9 + 0,4a = 0
<=> 0,4a = 0,9
<=> a = 2,25
Es herrscht ein faires Spiel, wenn bei zwei gleichen Zahlen ein Betrag von 2,25 € ausbezahlt wird!
x |
3 |
4 |
5 |
6 |
7 |
P(X=x) |
Histogramm:
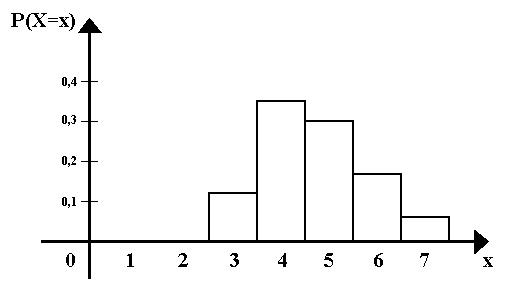
Die mittlere Keimdauer entspricht dem Erwartungswert E(X) der Zufallsgröße X.
E(X) = 3 * 0,12 + 4 * 0,35 + 5 * 0,30 + 6 * 0,17 + 7 * 0,06 = 4,7
Es soll gelten:
P( | X - E(X) | ) < 0,20 * E(X)
= P ( | X - 4,7 | ) < 0,94
= P ( -0,94 < X - 4,7 < 0,94)
= P ( 4,7 - 0,94 < X < 4,7 + 0,94)
= P ( 3,76 < X < 5,64 )
= P(X=4) + P(X=5)
= 0,35 + 0,30 = 0,65
x |
1 |
3 |
8 |
10 |
| P(X=x) |
Histogramm:
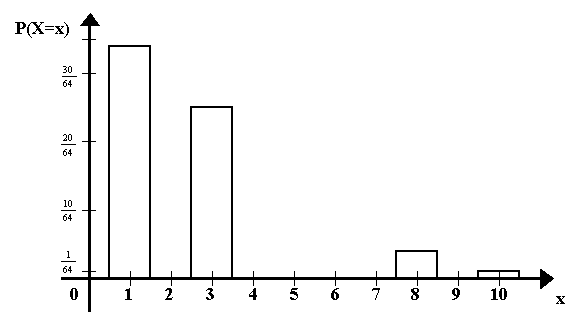
E(X) = 1 * ![]() +
3 *
+
3 *![]() +
8 *
+
8 * ![]() +
10 *
+
10 *![]() =
2,36
=
2,36
Var(X) = 12 * ![]() +
32 *
+
32 *![]() + 82 *
+ 82 * ![]() + 102 *
+ 102 *![]() - 2,362 = 4,04
- 2,362 = 4,04
![]()
Aus der Normierungsbedingung ![]() =
1 folgt:
=
1 folgt:
I) a + 0,25 + 3b + 0,1 + b + 0,05 = 1  a = - 4b + 0,6
a = - 4b + 0,6
Außerdem gilt:
II) a + 0,25 + 3b = 0,8
Jetzt kann I in II eingesetzt werden:
- 4b + 0,6 + 0,25 + 3b = 0,8  b =
0,05
b =
0,05
Jetzt kann b in I eingesetzt werden:
a = - 4 × 0,05 + 0,6  a = 0,4
a = 0,4
E(X) = 0 * 0,4 + 1 * 0,25 + 2 * 0,15 + 3 * 0,1 + 4 *0,05 * 5 × 0,05 = 1,3
Var (X) = 02 * 0,4 + 12 * 0,25 + 22 * 0,15 + 32 * 0,1 + 42 * 0,05 + 52 * 0,05 - 1,32 = 2,11
σ = ![]() =
1,45
=
1,45
Wegen | X - µ | < σ folgt:
| X - 1,3 | < 1,45
 - 1,45 < X - 1,3 < 1,45
- 1,45 < X - 1,3 < 1,45
 - 1,45 + 1,3 < X < 1,45 + 1,3
- 1,45 + 1,3 < X < 1,45 + 1,3
 - 0,15 < X < 2,75
- 0,15 < X < 2,75
P ( | X - µ | < σ ) = P(X=0) + P(X=1) + P(X=2)
P ( | X - µ |
< σ ) = 0,4 + 0,25 + 0,15 = 0,8
Aus der Normierungsbedingung ![]() = 1 folgt:
= 1 folgt:
I) 20a + 5b + 2b + a = 1  21a + 7b = 1
21a + 7b = 1
Mit E(X) = 1 folgt:
II) 0 * 20a + 1* 5b + 2 * 2b + 3 * a = 1  9b + 3a = 1
9b + 3a = 1
Aus I. folgt ![]() ,
eingesetzt in II. ergibt:
,
eingesetzt in II. ergibt:
II) ![]()
 63b + 1 - 7b = 7
63b + 1 - 7b = 7 
![]()
Eingesetzt in I. ergibt
I) 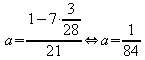
x |
0 |
1 |
2 |
3 |
P(X=x) |
Histogramm:
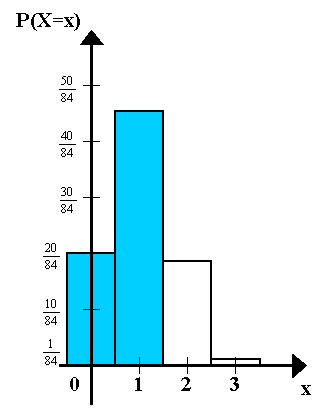
Aus der Normierungsbedingung ![]() = 1 folgt:
= 1 folgt:
0,4a + 0,025a2 + 0,05 + 0,05 = 1
 0,025a2 + 0,4a - 0,9 = 0
0,025a2 + 0,4a - 0,9 = 0
 a2 + 16a - 36 = 0
a2 + 16a - 36 = 0
 (a + 18) (a - 2) = 0
(a + 18) (a - 2) = 0
 a = 2
a = 2
(a = -18 scheidet aus, da es keine negativen Wahrscheinlichkeiten gibt.)
E(X) = 0 * 0,4 * 2 + 1 * 0,025 * 22 + 2 * 0,05 + 3 * 0,05 = 0,35
Var(X) = 02 * 0,4 * 2 + 12 * 0,025 * 22 + 22 * 0,05 + 32 * 0,05 - 0,352 = 0,63
![]()
P(E(X)-2σ ≤ X ≤ E(X)+2σ) =
= P(-1,23 ≤ X ≤
1,93) = P(X=0) + P(X=1) = 0,8 + 0,1 = 0,9