3. Ebenen im Raum
Wie auch bei einer Geraden braucht man für die eindeutige Darstellung einer Ebene einen beliebigen Punkt P der Ebene, als Stützpunkt. Desweiteren benötigt man zwei Richtungsvektoren: 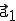 und
und 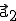 , welche nicht linear abhängig (nicht parallel) sein dürfen.
Streckt man vom Punkt P aus die Richtungsvektoren um reelle Streckungsfaktoren
, welche nicht linear abhängig (nicht parallel) sein dürfen.
Streckt man vom Punkt P aus die Richtungsvektoren um reelle Streckungsfaktoren 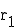 und
und 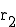 , so kann man jeden beliebigen Punkt in der Ebene erreichen.
, so kann man jeden beliebigen Punkt in der Ebene erreichen.
Daraus ergibt sich dann die folgende Formel: 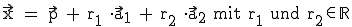 .
.
Hinweis: Sind statt 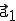 und
und 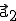 zwei weitere Ebenenpunkte Q und R gegeben, so kann man mit Hilfe von P, Q und R die beiden Richtungsvektoren
zwei weitere Ebenenpunkte Q und R gegeben, so kann man mit Hilfe von P, Q und R die beiden Richtungsvektoren 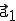 und
und 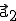 leicht bestimmen:
leicht bestimmen: 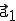 =
= 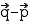 ;
; 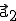 =
= 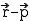 .
.
Beispiele:
Gegeben ist die die Ebene E: 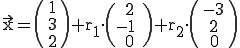 .
.
Für 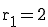 und
und 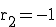 soll nun der dazu gehörige Punkt
soll nun der dazu gehörige Punkt 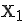 gefunden werden:
gefunden werden:
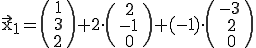
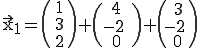
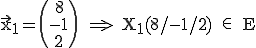
Es sollen 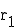 und
und 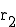 so bestimmt werden, dass der Punkt
so bestimmt werden, dass der Punkt 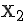 (4 / 0 / 2) auf der Ebene E liegt:
(4 / 0 / 2) auf der Ebene E liegt:
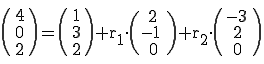
Dies wandelt man in drei Gleichungen (ein Gleichungssystem) um:
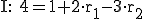
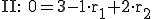
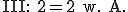
Nun eliminiert man den Parameter 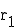 in dem man II mit 2 multipliziert. Durch das Additionsverfahren fällt
in dem man II mit 2 multipliziert. Durch das Additionsverfahren fällt 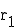 weg:
weg:
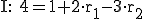
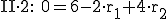
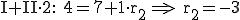
Man setzt 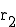 in II und löst nach
in II und löst nach 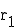 auf:
auf:
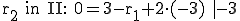
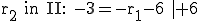
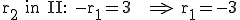
Für 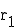 =–3 und
=–3 und 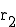 =–3 ist
=–3 ist 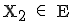 .
.
Siehe auch: Applets "Vektorielle Ebenendarstellung", "Ebenen bestimmen" und "Ebenengleichung"
Die allgemeine Koordinatenform sieht wie folgt aus: 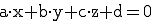
Sie gilt nur für die Ebene (nicht für die Gerade) im Raum.
Beispiele:
Gegeben ist die Ebene E: 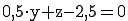
Prüfen Sie, ob der Punkt 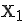 (4 / 3 / 1) auf der Ebene liegt.
(4 / 3 / 1) auf der Ebene liegt.
Man setzt den Punkt 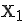 in die Koordinatenform der Ebene ein:
in die Koordinatenform der Ebene ein:
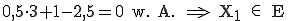
Bestimmen Sie die y-Koordinate von 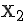 (2 / y / 3) so, dass der Punkt auf der Ebene E liegt:
(2 / y / 3) so, dass der Punkt auf der Ebene E liegt:
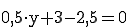
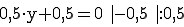
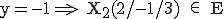
3.3 Umwandlung der Vektorform in die Koordinatenform
Man wandelt die Vektorform in ein Gleichungssystem von 3 Gleichungen mit 5 Unbekannten um (siehe Geraden im Raum oder in der Ebene), stellt den Stützvektor auf die andere Seite und wendet das Gauß-Verfahren an, mit dem man die beiden Streckungsfaktoren (Parameter) eliminiert.
Beispiel:
Die Vektorform der Ebene E soll in die Koordinatenform umgewandelt werden: 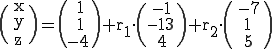
Nun stellt man den Stützvektor auf die andere Seite:
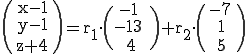
Man erstellt drei Gleichungen (ein Gleichungssystem):
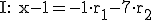
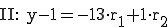
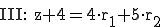
Dann wendet man auf diese drei Gleichungen das Gauß-Verfahren an, um r1 und r2 zu eliminieren:
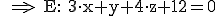
3.4 Umwandlung der Koordinatenform in die Vektorform
Um die Vektorform angeben zu können, benötigen wir einen Stützpunkt der Ebene und zwei nicht linear abhängige (nicht parallele) Richtungsvektoren. Insgesamt reicht es uns, wenn wir drei Punkte der Ebene kennen, die nicht auf einer Geraden liegen. Diese Punkte erhalten wir, indem wir in die Koordinatenform 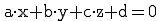 dreimal für jeweils zwei der drei Variablen x, y und z eine Zahl einsetzen und dann die übrige ermitteln. Günstig ist es, jeweils Null einzusetzen, weil wir dann Rechenschritte sparen können. Haben wir die drei Punkte, so wählen wir einen als Stützpunkt und errechnen außerdem zwei Richtungsvektoren (Spitze minus Fuß).
dreimal für jeweils zwei der drei Variablen x, y und z eine Zahl einsetzen und dann die übrige ermitteln. Günstig ist es, jeweils Null einzusetzen, weil wir dann Rechenschritte sparen können. Haben wir die drei Punkte, so wählen wir einen als Stützpunkt und errechnen außerdem zwei Richtungsvektoren (Spitze minus Fuß).
Beispiel 1: Aus der Koordinatenform 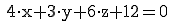 soll die Vektorform ermittelt werden.
soll die Vektorform ermittelt werden.
Wir berechnen nun drei Punkte, die ich hier A, B und C nenne:
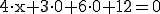
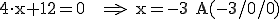
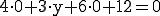
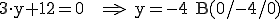
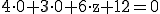
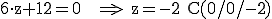
Nun verwenden wir z. B. A als Stützpunkt und berechnen die Richtungsvektoren 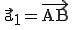 und
und 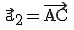 :
:
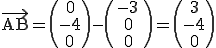
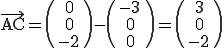
Wenn wir nun die beiden Richtungsvektoren und den Stützpunkt A in unsere Gleichung 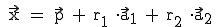 einsetzen erhalten wir:
einsetzen erhalten wir:
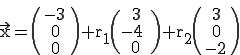
Beispiel 2: Die Koordinatenform 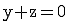 soll in die Vektorform umgewandelt werden. Auffällig ist, dass wir kein
soll in die Vektorform umgewandelt werden. Auffällig ist, dass wir kein 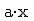 und kein d haben. Das fehlende d bedeutet d = 0, d. h. die Ebene verläuft durch den Ursprung. Für das fehlende x können wir bei allen drei Punkten eine beliebige Zahl verwenden:
und kein d haben. Das fehlende d bedeutet d = 0, d. h. die Ebene verläuft durch den Ursprung. Für das fehlende x können wir bei allen drei Punkten eine beliebige Zahl verwenden:

Da x frei wählbar ist, liegt dann auch B(1 / 0 / 0) auf der Ebene.
Nun setzen wir für z zum Beispiel 1 ein:
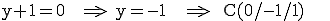 (x = 0 ist frei gewählt.)
(x = 0 ist frei gewählt.)
Jetzt verwenden wir z. B. A als Stützpunkt und berechnen die Richtungsvektoren 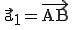 und
und 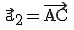 :
:
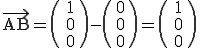
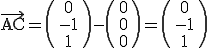
Die Ebenengleichung lautet also:
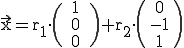
Eine Ebene kann folgende besondere Lagen im Raum annehmen:
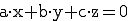 .
.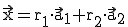 .
.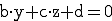 , da a = 0.
, da a = 0.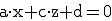 , da b = 0.
, da b = 0.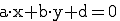 , da c = 0.
, da c = 0.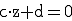
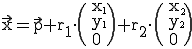
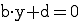
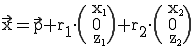
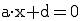
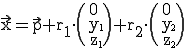
Die Ebene kann auch durch den Ursprung verlaufen und parallel z. B. zur x-Achse verlaufen, diese also einschließen. In diesem Fall kombiniert man die beiden Gleichungen. Es fallen x und d weg : 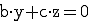
Ebenfalls kann die Ebene durch den Ursprung verlaufen und parallel zu einer Basisebene, z. B. zur xy-Ebene, verlaufen. Es handelt sich in diesem Fall also um die xy-Ebene. In diesem Fall fallen x, y und d weg: 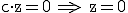 .
.
| Zurück zur Übersicht |