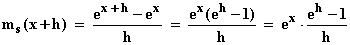Für die Basis a kommen nur positive reelle Zahlen in Betracht, d. h.  IR+.
IR+.
Gegenbeispiel:
a = –1, x = ½ :
ax = (–1)½ ist in IR nicht definiert, denn es gibt keine reelle Wurzel aus –1.
Grafen:
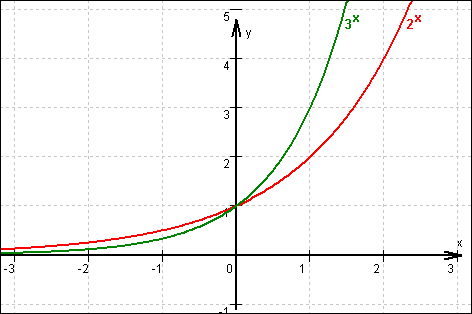
Beschreibung:
Beide Grafen verlaufen nur durch den 1. und 2. Quadranten, haben die
Vergleich:
Die Ordinaten des Grafen von f(x) = 3x streben im Vergleich zu
Erstens fällt auf, dass die Ableitungsgrafen prinzipiell den selben Verlauf haben wie die Ausgangsgrafen. Offensichtlich handelt es sich bei den Ableitungen ebenfalls um Exponentialfunktionen.
Zweitens fällt auf, dass sich die Ableitungsgrafen den Ausgangsgrafen für wachsende Basiswerte
4.2
Da für h  0 der Differenzenquotient
0 der Differenzenquotient  gegen die Ableitung von
gegen die Ableitung von  ,
,
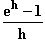 für h
für h  0 gegen 1 streben.
0 gegen 1 streben.
Also:
h  0
0 
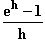
 1
1
Grenzwert für e:
Für die folgenden Überlegungen gelte h ≈ 0.
Dann gilt:
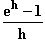 ≈ 1
≈ 1
 eh – 1 ≈ h
eh – 1 ≈ h
 eh ≈ 1 + h
eh ≈ 1 + h
 e ≈
e ≈ 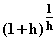
Bestimmung der Zahl e:
| n | 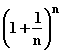 |
| 1 | 2 |
| 2 | 2,25 |
| 4 | 2,44 |
| 8 | 2,56 |
| 16 | 2,64 |
| 32 | 2,68 |
| 64 | 2,70 |
| 128 | 2,708 |
| 256 | 2,713 |
| 1024 | 2,717 |
| 2048 | 2,718 |
| 4096 | 2,718 |
 e ≈ 2,718
e ≈ 2,718
5.1
Da g(f(x)) = x gelten soll, ist die gesuchte Funktion g die Umkehrfunktion von f. Um die Gleichung von g zu ermitteln, müssen also bei der Funktion f x und y vertauscht werden:
f: y = 2x – 3 

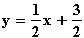
Probe:
g(f(x)) = 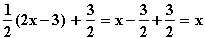
Grafen von f und g:
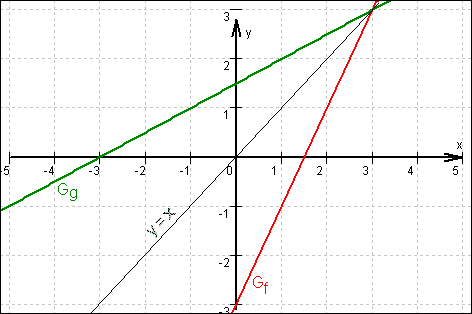
Beziehung zwischen den Grafen:
Wie bei den Grafen einer Funktion und ihrer Umkehrfunktion üblich, sind sie Spiegelbilder bezüglich der Winkelhalbierenden des 1. und 3. Quadranten, also der Geraden
Wenn sie in ihrem gesamten Definitionsbereich echt monoton steigt oder fällt.
Weil sie in ihrem gesamten Definitionsbereich echt monoton steigen.
Wertetabelle:
| x | g(x) |
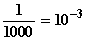 |
–3 |
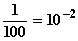 |
–2 |
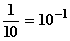 |
–1 |
| 1 = 100 | 0 |
| 10 = 101 | 1 |
| 100 = 102 | 2 |
| 1000 = 103 | 3 |
Wirkung von g:
Schreibt man das Argument von g als Zehnerpotenz, so liefert die Funktion g den Exponenten dieser Zehnerpotenz zurück.
Die max. Definitionsmenge einer Logarithmusfunktion ist gleich der Wertemenge der zugehörigen Exponentialfunktion, also stets IR+.
logax = 0 | a( )
 x = a0 = 1
x = a0 = 1
Die gemeinsame Nullstelle aller Logarithmusfunktionen lautet also
9.1
9.2
f(x) = ex2+1 – e2 = 0
 ex2+1 = e2 | ln ( )
ex2+1 = e2 | ln ( )
 x2+1 = 2
x2+1 = 2
 x2 = 1
x2 = 1
 x1/2 = ± 1
x1/2 = ± 1
9.3
f(x) = e2x – ex – 2 = 0
 (ex)2 – ex – 2 = 0
(ex)2 – ex – 2 = 0
Substitution: ex = z
 z2 – z – 2 = 0
z2 – z – 2 = 0
 z
z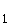 = –1; z
= –1; z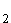 = 2
= 2
Rücksubstitution: z = ex
 ex = –1: keine Lösung, da ln(-1) nicht def.;
ex = –1: keine Lösung, da ln(-1) nicht def.;
ex = 2  x = ln 2
x = ln 2
9.4
f(x) = 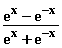 = 0
= 0
 ex – e–x = 0
ex – e–x = 0
 ex = e–x | ln ( )
ex = e–x | ln ( )
 x = –x
x = –x
 2x = 0
2x = 0
 x = 0
x = 0
11.1
Grenzwert von f für x  0 durch Kürzen:
0 durch Kürzen:
f(x) = 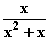 =
= 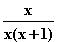

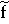 (x) =
(x) = 

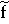 (0) = 1
(0) = 1
Also ergibt sich durch Kürzen von f: 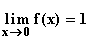 .
.
Grenzwert von f für x  0 mit der Regel von de L'Hospital:
0 mit der Regel von de L'Hospital:
f1(x) = x  0; f2(x) = x2 + x
0; f2(x) = x2 + x  0
0

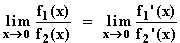
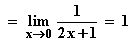
11.2
Grenzwert von f(x) = 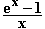 für x
für x  0:
0:
f1(x) = ex – 1  0; f2(x) = x
0; f2(x) = x  0
0

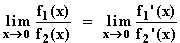
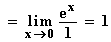
12.
Grenzwert von f(x) = 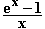 für x
für x  ∞ :
∞ :
f1(x) = ex – 1  ∞; f2(x) = x
∞; f2(x) = x  ∞
∞

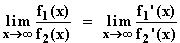
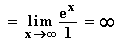
Grenzwert für x  –∞ :
–∞ :
f1(x) = ex – 1; f2(x) = x
Hier sind die Voraussetzungen für die Regel von de L'Hospital nicht erfüllt, denn  –∞
–∞ –1.
–1.
Wenn der Zähler eines Bruches gegen einen konstanten Wert und der Nenner gegen –∞ streben, dann strebt der Bruch gegen 0.
 Für x
Für x  –∞ gilt f(x)
–∞ gilt f(x)  0.
0.
13.1
Verhalten von f(x) für x  ± ∞ :
± ∞ :
f(x) = 
 ± ∞
± ∞
Verhalten von f(x) für x  0 :
0 :
f(x) = 
 0
0
Verhalten von f(x) für x  0 :
0 :
f(x) = 
 ??
??
f(x) = 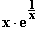 =
= 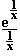
f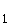 (x) =
(x) =  ; f
; f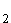 (x) =
(x) = 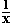
f1(x)  ∞; f2(x)
∞; f2(x)  ∞
∞
Anwendung der Regel von de L'Hospital:
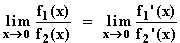
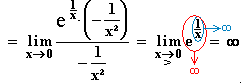
13.2
13.3
Skizze des Grafen von f:
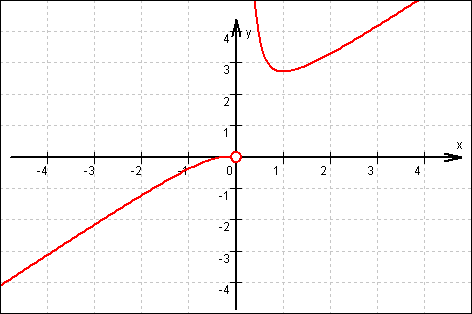
14.1
a) ∫exdx = ex + c, c  IR.
IR.
b) ∫e2xdx = 0,5·e2x + c, c  IR.
IR.
c) ∫e–x+1dx = –e–x+1 + c, c  IR.
IR.
14.2
∫eax+bdx =  eax+b + c, c
eax+b + c, c  IR.
IR.