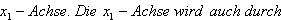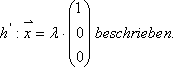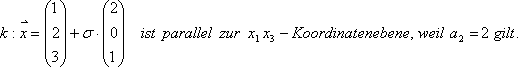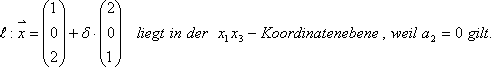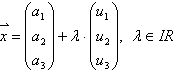die
Parameterdarstellung einer Raumgeraden.2. Besondere Lagen von Geraden und Ebenen im Koordinatensystem
2.1 Besondere Lagen von Geraden im IR3
Es sei 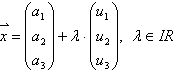die
Parameterdarstellung einer Raumgeraden.
Fall 1: Gerade ist parallel zu einer Koordinatenebene:
Eine der Koordinaten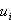 
des
Richtungsvektors ist Null, z. B.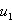 
=
0 .
Die Gerade ist dann wegen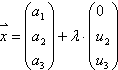 
echt parallel zur 
≠
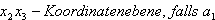0,
sie liegt in der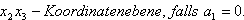 
Fall 2: Gerade ist parallel zu einer Koordinatenachse:
Zwei Koordinaten 
.
Die Lage von g im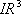 
wird
also bestimmt durch die Indizes der Koordinaten des
Richtungsvektors , die ungleich Null sind.
Die Entscheidung “echt parallel“
wird durch die Koordinaten des Antragspunkts bestimmt.
Beispiele:
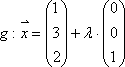ist
echt parallel zur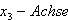 
, da
.
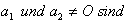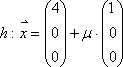ist
eine mögliche Gleichung für die 
