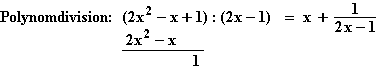Der Natürliche Logarithmus von x, kurz: ln x, ist die Umkehrfunktion der Exponentialfunktion f(x) = ex.
Es gilt also: ln(ex) = x für alle x  IR sowie eln x = x für alle x
IR sowie eln x = x für alle x  IR+.
IR+.
1.2
Die Grafen der e-Funktion und des natürlichen Logarithmus sind Spiegelbilder zueinander, und zwar bzgl. der Geraden y = x.
1.3
1.4
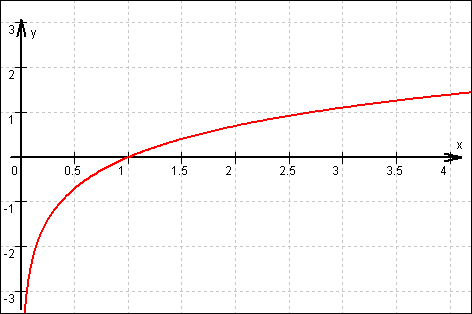
Die Funktion f(x) = ln x hat folgende Eigenschaften:
• Die Definitionsmenge ist IR+, die Wertemenge IR.
• Ihr Graf hat die senkrechte Asymptote x = 0.
• Die einzige Nullstelle ist x = 1.
• Für 0 < x < 1 hat sie negative Werte, für x > 1 positive Werte.
• Für x  +0 strebt sie nach –∞; für x
+0 strebt sie nach –∞; für x  +∞ strebt sie nach +∞.
+∞ strebt sie nach +∞.
• In ihrer gesamten Definitionsmenge steigt sie streng monoton.
• Ihr Graf ist überall rechtsgekrümmt.
2.1
f(x) = ln x – 1 ist nur für x > 0 definiert, d. h. IDf = IR+.
Nullstelle: ln x – 1 = 0  ln x = 1
ln x = 1  eln x = e1
eln x = e1  x = e
x = e
2.2
 ]1 ; +∞[.
]1 ; +∞[.
Nullstellen:
ln(x2–1) – ln 3 = 0  ln(x2–1) = ln 3
ln(x2–1) = ln 3  x2–1 = 3
x2–1 = 3  x2 = 4
x2 = 4  x1/2 = ±2
x1/2 = ±2
2.3
Nullstellen: (ln x)2 + ln x – 2 = 0
Substitution: ln x = z  z2 + z – 2 = 0
z2 + z – 2 = 0  z1 = 1; z2 = –2
z1 = 1; z2 = –2
Rücksubstitution: z = ln x, also ln x = 1  x
x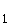 = e
= e
oder ln x = –2  x
x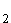 =
= 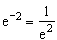
2.4

 ID
ID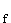 = ]–∞ ; –
= ]–∞ ; – [
[  ]0 ; +∞[.
]0 ; +∞[.
Nullstellen:
(x2 – 1)·ln(x2 + 1,5x) = 0  x2 – 1 = 0
x2 – 1 = 0  ln(x2 + 1,5x) = 0
ln(x2 + 1,5x) = 0
x2 = 1  x2 + 1,5x = e0 = 1
x2 + 1,5x = e0 = 1
x2 + 1,5x – 1 = 0
x1 = –1  IDf x3 = –2
IDf x3 = –2  IDf
IDf
x2 = 1  IDf x4 = 0,5
IDf x4 = 0,5  IDf
IDf
Die Nullstellen sind also –2, 0,5 und 1.
Erste Darstellung von f: Zweite Darstellung von f:
f(x) = x  f(x) = eln x
f(x) = eln x 
f '(x) = 1 f '(x) = eln x·(ln x)' = x·(ln x)'
Also gilt: 1 = x·(ln x)' 

4.
 f '(x) =
f '(x) = 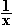
f(x) = ln(x –1) – ln 3
–1) – ln 3  f '(x) =
f '(x) = 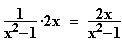
f(x) = (ln x) + ln x – 2
+ ln x – 2  f '(x) = 2(ln x)·
f '(x) = 2(ln x)·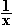 +
+ 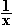 =
= 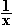 (1 + 2 ln x)
(1 + 2 ln x)
f(x) = (x – 1) · ln (x
– 1) · ln (x + 1,5x)
+ 1,5x)  f '(x) = 2x · ln (x
f '(x) = 2x · ln (x + 1,5x) + (x
+ 1,5x) + (x – 1) ·
– 1) ·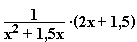
5.
Für a  IR+, m,n
IR+, m,n  IR, p = am, q = an gilt:
IR, p = am, q = an gilt:
| am·an = am+n | am:an = am–n | (am)n = am·n |
| log (p · q) = log p + log q | log (p : q) = log p – log q | log (pn) = n · log p |
6.1
Da g(x) = ln 2x = ln 2 + ln x = f(x) + ln 2 gilt, geht der Graf von g aus dem Grafen von f durch Verschiebung um ln 2 nach oben hervor.
6.2
Für x > 0 sind die Terme ln x² und 2 ln x identisch, haben also die selben Grafen. Für
Da f(x) = ln x² einen zur y-Achse symmetrischen Grafen hat, lässt sich also folgern, dass der Graf von g nur aus dem rechten Ast des Grafen von f besteht:
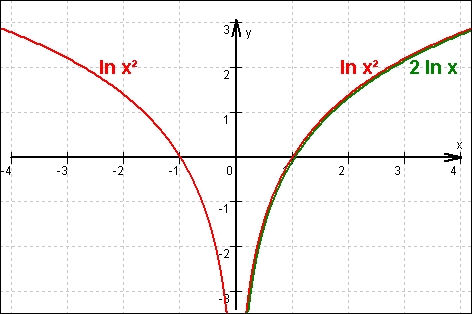
6.3
Die Betragsstriche erweitern den Definitionsbereich von g von IR+auf IR\{0}, so dass jetzt die Grafen von f und g übereinstimmen.
7.
Widerlegung:
f(x) = ln 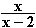 ; g(x) = ln x – ln (x – 2)
; g(x) = ln x – ln (x – 2) 
IDf = ]–∞; 0[  ]2; +∞[ ; IDg = ]2; +∞[ .
]2; +∞[ ; IDg = ]2; +∞[ .
Da die Definitionsbereiche nicht übereinstimmen, ist die Behauptung f = g falsch.
Die Behauptung lässt sich aber korrigieren:
Innerhalb der Definitionsmenge von f stimmen die Terme ln 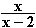 , ln |
, ln |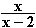 | und
| und
8.1
f(x) = 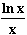 hat die Definitionsränder 0 und +∞ .
hat die Definitionsränder 0 und +∞ .
Für x > 0 gilt: 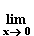
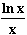 = – ∞ .
= – ∞ .
Für x  ∞ gelten für f die Voraussetzungen von de L'Hospital:
∞ gelten für f die Voraussetzungen von de L'Hospital:
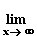
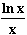 =
= 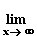
 = 0.
= 0.
8.2
f(x) = 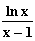 hat die Definitionsränder 0, 1 und +∞ .
hat die Definitionsränder 0, 1 und +∞ .
Für x > 0 gilt: 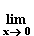
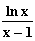 = + ∞ .
= + ∞ .
Für x  1 gelten für f die Voraussetzungen von de L'Hospital:
1 gelten für f die Voraussetzungen von de L'Hospital:
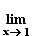
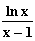 =
= 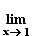
 = 1.
= 1.
Für x  ∞ gelten für f auch die Voraussetzungen von de L'Hospital:
∞ gelten für f auch die Voraussetzungen von de L'Hospital:
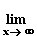
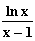 =
= 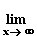
 = 0.
= 0.
8.3
f(x) = x · ln x hat die Definitionsränder 0 und +∞ .
Für x  +0 gelten für f nach Umwandlung in einen Quotienten die Voraussetzungen von de L'Hospital:
+0 gelten für f nach Umwandlung in einen Quotienten die Voraussetzungen von de L'Hospital:
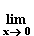 (x · ln x) =
(x · ln x) = 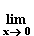
 =
= 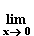
 =
= 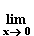 (–x) = 0.
(–x) = 0.
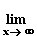 (x · ln x) = + ∞ .
(x · ln x) = + ∞ .
9.1
a) ∫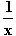 dx = ln x + c für x > 0
dx = ln x + c für x > 0
b) ∫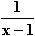 dx = ln (x–1) + c für x > 1
dx = ln (x–1) + c für x > 1
c) ∫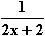 dx =
dx =  ln (2x+2) + c für x > –1
ln (2x+2) + c für x > –1
d) ∫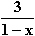 dx = –3 ln (1–x) + c für x < 1
dx = –3 ln (1–x) + c für x < 1
9.2
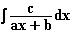 =
= 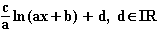
10.1
a) (ln x)' = 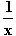 für x > 0; b) (ln (–x))' =
für x > 0; b) (ln (–x))' =  für x < 0
für x < 0
c) (ln (x–1))' = 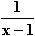 für x > 1; d) (ln (1–x))' =
für x > 1; d) (ln (1–x))' =  für x < 1
für x < 1
e) (ln (2x+4))' =  für x > –2;
für x > –2;
f) (ln (–2x–4))' =  für x < –2
für x < –2
10.2
a) f(x) = 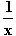 , x
, x  IR\{0}
IR\{0} 
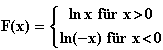
b) f(x) = 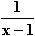 , x
, x  IR\{1}
IR\{1} 
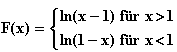
c) f(x) = 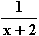 , x
, x  IR\{–2}
IR\{–2} 
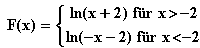
d) f(x) = 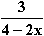 , x
, x  IR\{2}
IR\{2} 
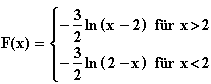
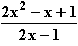 dx für x > 0,5
dx für x > 0,5