| 13. Klasse |
2. Schulaufgabe |
Lineare Algebra |
2006/07 |
1.0 Gegeben seien die Vektoren 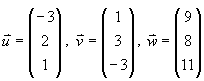 .
1.1 Untersuchen Sie, ob die Vektoren
.
1.1 Untersuchen Sie, ob die Vektoren 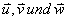 eine Basis des
eine Basis des 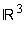 bilden .
1.2 Durch obige Angaben ist der abgebildete Quader eindeutig festgelegt . O bezeichnet dabei den Ursprung des
Koordinatensystems.
bilden .
1.2 Durch obige Angaben ist der abgebildete Quader eindeutig festgelegt . O bezeichnet dabei den Ursprung des
Koordinatensystems.
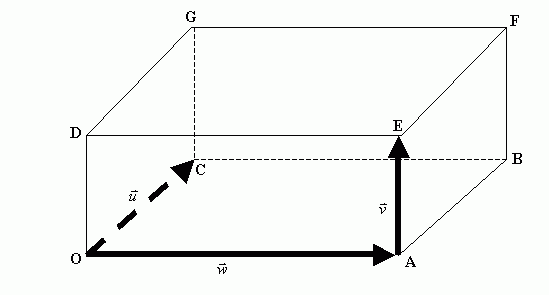 Bestimmen Sie die Koordinaten des Eckpunktes B , des Mittelpunktes MEF der Kante [EF] und des
Diagonalenschnittpunkts S der Bodenfläche OABC .
1.3 Bestimmen Sie k so, dass sich der Vektor
Bestimmen Sie die Koordinaten des Eckpunktes B , des Mittelpunktes MEF der Kante [EF] und des
Diagonalenschnittpunkts S der Bodenfläche OABC .
1.3 Bestimmen Sie k so, dass sich der Vektor 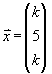 als Linearkombination von
als Linearkombination von 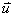 und
und 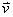 darstellen lässt .
Geben Sie diese Linearkombination an und fertigen Sie eine Skizze an , aus der die gegenseitige Lage der
drei Vektoren ersichtlich ist .
2. Geben Sie ein Gleichungssystem bestehend aus drei Gleichungen mit jeweils drei Unbekannten (alle Ko-
effizienten ≠ 0) an , das nicht lösbar ist und begründen Sie kurz , warum das gewählte Gleichungssystem
unlösbar sein muss .
darstellen lässt .
Geben Sie diese Linearkombination an und fertigen Sie eine Skizze an , aus der die gegenseitige Lage der
drei Vektoren ersichtlich ist .
2. Geben Sie ein Gleichungssystem bestehend aus drei Gleichungen mit jeweils drei Unbekannten (alle Ko-
effizienten ≠ 0) an , das nicht lösbar ist und begründen Sie kurz , warum das gewählte Gleichungssystem
unlösbar sein muss .
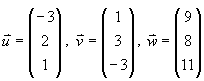 .
1.1 Untersuchen Sie, ob die Vektoren
.
1.1 Untersuchen Sie, ob die Vektoren 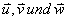 eine Basis des
eine Basis des 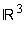 bilden .
1.2 Durch obige Angaben ist der abgebildete Quader eindeutig festgelegt . O bezeichnet dabei den Ursprung des
Koordinatensystems.
bilden .
1.2 Durch obige Angaben ist der abgebildete Quader eindeutig festgelegt . O bezeichnet dabei den Ursprung des
Koordinatensystems.
 Bestimmen Sie die Koordinaten des Eckpunktes B , des Mittelpunktes MEF der Kante [EF] und des
Diagonalenschnittpunkts S der Bodenfläche OABC .
1.3 Bestimmen Sie k so, dass sich der Vektor
Bestimmen Sie die Koordinaten des Eckpunktes B , des Mittelpunktes MEF der Kante [EF] und des
Diagonalenschnittpunkts S der Bodenfläche OABC .
1.3 Bestimmen Sie k so, dass sich der Vektor 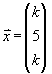 als Linearkombination von
als Linearkombination von 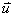 und
und 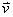 darstellen lässt .
Geben Sie diese Linearkombination an und fertigen Sie eine Skizze an , aus der die gegenseitige Lage der
drei Vektoren ersichtlich ist .
2. Geben Sie ein Gleichungssystem bestehend aus drei Gleichungen mit jeweils drei Unbekannten (alle Ko-
effizienten ≠ 0) an , das nicht lösbar ist und begründen Sie kurz , warum das gewählte Gleichungssystem
unlösbar sein muss .
darstellen lässt .
Geben Sie diese Linearkombination an und fertigen Sie eine Skizze an , aus der die gegenseitige Lage der
drei Vektoren ersichtlich ist .
2. Geben Sie ein Gleichungssystem bestehend aus drei Gleichungen mit jeweils drei Unbekannten (alle Ko-
effizienten ≠ 0) an , das nicht lösbar ist und begründen Sie kurz , warum das gewählte Gleichungssystem
unlösbar sein muss .
