13. Klasse 3. Schulaufgabe
Analysis 2007/08
Lösungen
1.1 Bestimmung von D(f)max:
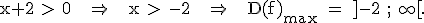 Schnittpunkte von G(f) mit den Achsen:
Schnittpunkte von G(f) mit den Achsen:
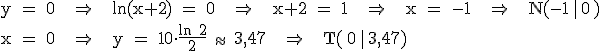 1.2
1.2 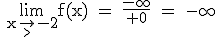
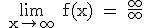 : nicht kalkulierbar, also mit de L'Hospital:
: nicht kalkulierbar, also mit de L'Hospital:
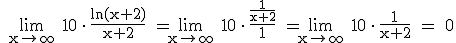 G(f) hat also zwei Asymptoten:
eine senkrechte Asymptote mit der Gleichung x = –2 ;
eine waagrechte Asymptote mit der Gleichung y = 0 .
1.3
G(f) hat also zwei Asymptoten:
eine senkrechte Asymptote mit der Gleichung x = –2 ;
eine waagrechte Asymptote mit der Gleichung y = 0 .
1.3 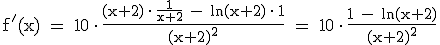
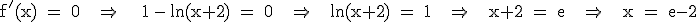
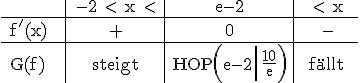 Näherungsweise hat der Hochpunkt die Koordinaten (0,72 | 3,68).
1.4 Graph von f:
Näherungsweise hat der Hochpunkt die Koordinaten (0,72 | 3,68).
1.4 Graph von f:
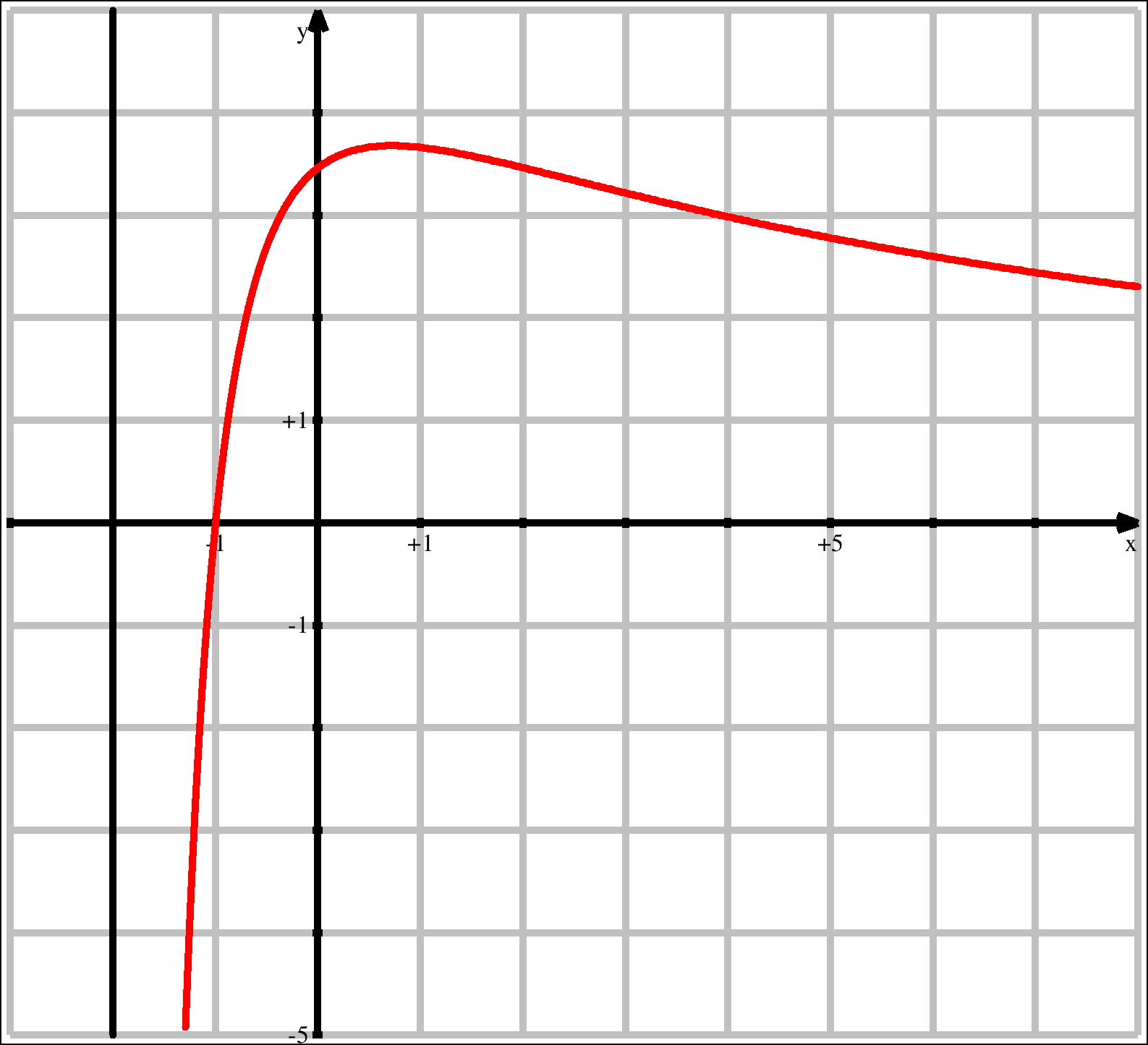 Da der Graph von f sich vom Hochpunkt aus asymptotisch der x-Achse annähert, muss er
dazwischen einen Wendepunkt haben. Einen weiteren hat er nicht.
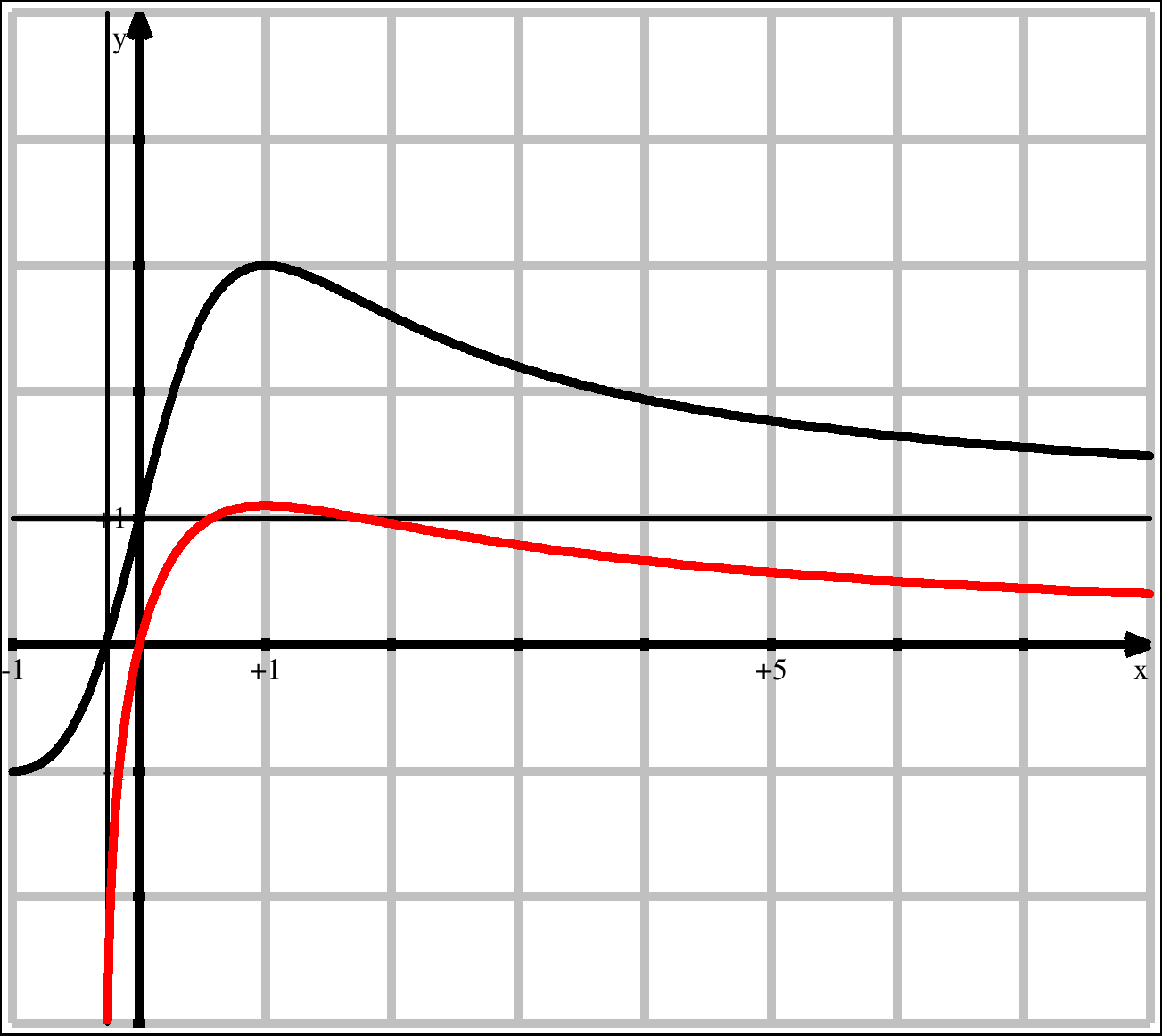
2.1 D(h) = ] –0,25 ; +∞[ (linke Grenze nach Augenmaß).
Nullstelle: x = 0
Hochpunkt: (1 | ln(3))
2.2 Senkrechte Asymptote: x = –0,25
Waagrechte Asymptote: y = ln 1 = 0
2.3 Graph von h (rot):
Da der Graph von f sich vom Hochpunkt aus asymptotisch der x-Achse annähert, muss er
dazwischen einen Wendepunkt haben. Einen weiteren hat er nicht.
2.1 D(h) = ] –0,25 ; +∞[ (linke Grenze nach Augenmaß).
Nullstelle: x = 0
Hochpunkt: (1 | ln(3))
2.2 Senkrechte Asymptote: x = –0,25
Waagrechte Asymptote: y = ln 1 = 0
2.3 Graph von h (rot):
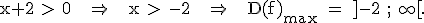 Schnittpunkte von G(f) mit den Achsen:
Schnittpunkte von G(f) mit den Achsen:
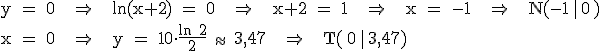 1.2
1.2 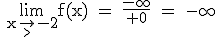
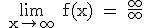 : nicht kalkulierbar, also mit de L'Hospital:
: nicht kalkulierbar, also mit de L'Hospital:
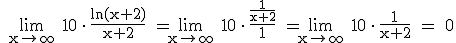 G(f) hat also zwei Asymptoten:
eine senkrechte Asymptote mit der Gleichung x = –2 ;
eine waagrechte Asymptote mit der Gleichung y = 0 .
1.3
G(f) hat also zwei Asymptoten:
eine senkrechte Asymptote mit der Gleichung x = –2 ;
eine waagrechte Asymptote mit der Gleichung y = 0 .
1.3 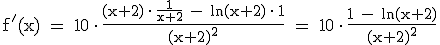
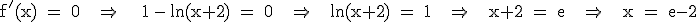
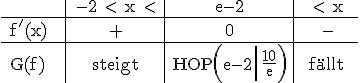 Näherungsweise hat der Hochpunkt die Koordinaten (0,72 | 3,68).
1.4 Graph von f:
Näherungsweise hat der Hochpunkt die Koordinaten (0,72 | 3,68).
1.4 Graph von f:
 Da der Graph von f sich vom Hochpunkt aus asymptotisch der x-Achse annähert, muss er
dazwischen einen Wendepunkt haben. Einen weiteren hat er nicht.
2.1 D(h) = ] –0,25 ; +∞[ (linke Grenze nach Augenmaß).
Nullstelle: x = 0
Hochpunkt: (1 | ln(3))
2.2 Senkrechte Asymptote: x = –0,25
Waagrechte Asymptote: y = ln 1 = 0
2.3 Graph von h (rot):
Da der Graph von f sich vom Hochpunkt aus asymptotisch der x-Achse annähert, muss er
dazwischen einen Wendepunkt haben. Einen weiteren hat er nicht.
2.1 D(h) = ] –0,25 ; +∞[ (linke Grenze nach Augenmaß).
Nullstelle: x = 0
Hochpunkt: (1 | ln(3))
2.2 Senkrechte Asymptote: x = –0,25
Waagrechte Asymptote: y = ln 1 = 0
2.3 Graph von h (rot):
