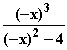 = –
= – 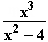 = –f(x)
= –f(x)  Gf ist punktsymmetrisch bzgl. des Koordinatenursprungs.
x = 2 ist Definitionslücke, da der Nenner dann 0 wird.
Verhalten von f bei x = 2:
Gf ist punktsymmetrisch bzgl. des Koordinatenursprungs.
x = 2 ist Definitionslücke, da der Nenner dann 0 wird.
Verhalten von f bei x = 2:Abschlussprüfung zur Erlangung der fachgebundenen Hochschulreife
Frühjahr 2001
A I: Lösungen
1.1 f(–x) == –
= –f(x)
Gf ist punktsymmetrisch bzgl. des Koordinatenursprungs. x = 2 ist Definitionslücke, da der Nenner dann 0 wird. Verhalten von f bei x = 2:
x < 2 < x
Zähler von f + 8 + Nenner von f – 0 + f(x) – –∞ / +∞ +
Wegen der Punktsymmetrie gibt es also zwei senkrechte Asymptoten mit den Gleichungen
x = –2 und x = 2.
Außerdem gibt es eine schiefe Asymptote, da der Zählergrad von f
um 1 größer ist als der Nennergrad.
Ihre Gleichung wird durch Polynomdivision ermittelt:
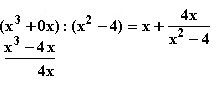
 Gleichung der schiefen Asymptote: y = x
1.2 f '(x) =
Gleichung der schiefen Asymptote: y = x
1.2 f '(x) = 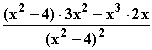 =
= 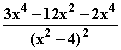 =
= 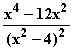 = 0
= 0
 x
x –12x
–12x = 0
= 0  x
x (x
(x –12) = 0
–12) = 0  x
x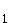

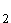 = 0; x
= 0; x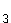

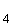 = ±
= ±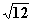 = ±2
= ±2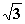 Der Nenner von f ' ist in IDf immer positiv. Also hängt das
Vorzeichen von f ' nur von seinem Zähler ab.
x
Der Nenner von f ' ist in IDf immer positiv. Also hängt das
Vorzeichen von f ' nur von seinem Zähler ab.
x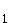

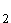 = 0 ist doppelte Nullstelle von f '
= 0 ist doppelte Nullstelle von f '  TEP(0 | 0)
Bei x
TEP(0 | 0)
Bei x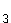 = 2
= 2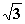 wechselt das Zählervorzeichen von – nach +
wechselt das Zählervorzeichen von – nach +  TIP(2
TIP(2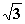 | 3
| 3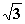 )
Punktsymmetrie von G
)
Punktsymmetrie von G bzgl. O
bzgl. O  HOP(–2
HOP(–2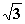 | –3
| –3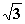 )
1.3
)
1.3 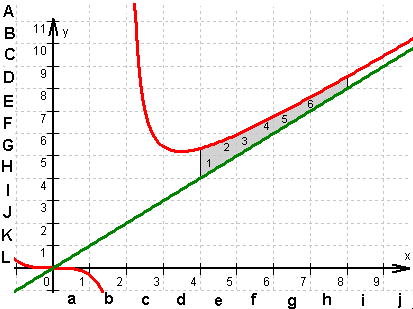 In der Grafik ist die durch das Integral
In der Grafik ist die durch das Integral 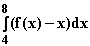 beschriebene
Fläche grau hervorgehoben. Diese Fläche lässt sich grob in halbe
Planquadrate mit dem Flächeninhalt 0,5 FE. zerlegen.
Da sich etwas mehr als 6 halbe Planquadrate ergeben, resultiert
für das Integral ein Wert von ca. 3.
1.4 F(x) = a·x
beschriebene
Fläche grau hervorgehoben. Diese Fläche lässt sich grob in halbe
Planquadrate mit dem Flächeninhalt 0,5 FE. zerlegen.
Da sich etwas mehr als 6 halbe Planquadrate ergeben, resultiert
für das Integral ein Wert von ca. 3.
1.4 F(x) = a·x + b·ln(x
+ b·ln(x – 4)
– 4) 
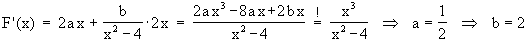 Die Fläche von 1.3 berechnet sich demnach wie folgt:
Die Fläche von 1.3 berechnet sich demnach wie folgt:
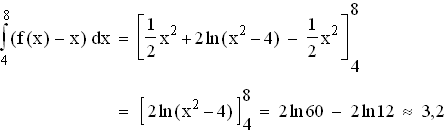 1.5 f(x) =
1.5 f(x) = 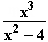 ; f
; f (x) =
(x) = 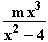 = m·f(x)
Für m > 0 gilt das Vorstehende mit der Abwandlung, dass die
schiefe Asymptote jetzt die Gleichung y = m·x hat und auch die
Ordinaten der Extrempunkte noch mit m multipliziert werden.
Für m > 1 sind alle Ordninaten im Vergleich zu denen der
Funktion f gestreckt, für 0 < m < 1 gestaucht.
Für m < 0 ist der Graph im Vergleich zu m > 0 an der x–Achse
gespiegelt, d. h., das Verhalten an den Definitionslücken dreht sich
um, und die Extrempunkte tauschen ihre Art.
2.1 Das Argument vom ln muss positiv und der Nenner darf nicht 0 sein
= m·f(x)
Für m > 0 gilt das Vorstehende mit der Abwandlung, dass die
schiefe Asymptote jetzt die Gleichung y = m·x hat und auch die
Ordinaten der Extrempunkte noch mit m multipliziert werden.
Für m > 1 sind alle Ordninaten im Vergleich zu denen der
Funktion f gestreckt, für 0 < m < 1 gestaucht.
Für m < 0 ist der Graph im Vergleich zu m > 0 an der x–Achse
gespiegelt, d. h., das Verhalten an den Definitionslücken dreht sich
um, und die Extrempunkte tauschen ihre Art.
2.1 Das Argument vom ln muss positiv und der Nenner darf nicht 0 sein  IDg = IR+ \ {1}
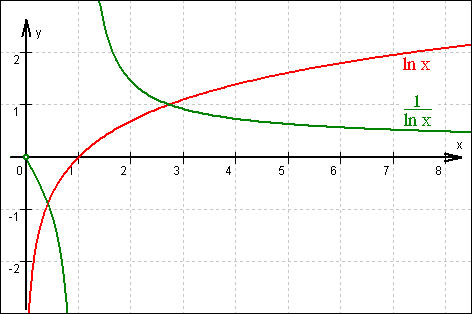
Skizze:
IDg = IR+ \ {1}
Skizze:
 Für x
Für x  0 gilt ln x
0 gilt ln x  –∞
–∞  g(x)
g(x)  – 0.
Für x
– 0.
Für x  ∞ gilt ln x
∞ gilt ln x  +∞
+∞  g(x)
g(x)  + 0.
Für x
+ 0.
Für x  1+ gilt ln x
1+ gilt ln x  0+
0+  g(x)
g(x)  + ∞.
Für x
+ ∞.
Für x  1- gilt ln x
1- gilt ln x  0-
0-  g(x)
g(x)  – ∞.
Da die ln-Funktion in ihrem Definitionsbereich überall steigt, muss g
als ihre Kehrwertfunktion überall fallen.
2.2
– ∞.
Da die ln-Funktion in ihrem Definitionsbereich überall steigt, muss g
als ihre Kehrwertfunktion überall fallen.
2.2 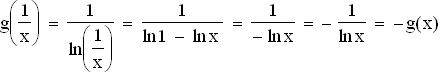
 Der Graf von g(
Der Graf von g(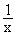 ) ist das Spiegelbild des Grafen von g an der x-Achse.
3.1
) ist das Spiegelbild des Grafen von g an der x-Achse.
3.1 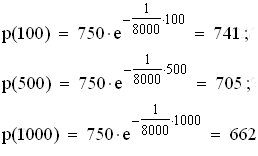 Alle Ergebnisse haben die Einheit hPa.
3.2
Alle Ergebnisse haben die Einheit hPa.
3.2 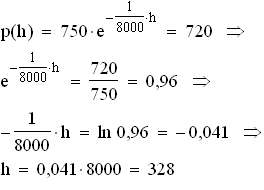 Der Bergsteiger befindet sich 328 m über dem Ausgangsniveau.
3.3
Der Bergsteiger befindet sich 328 m über dem Ausgangsniveau.
3.3 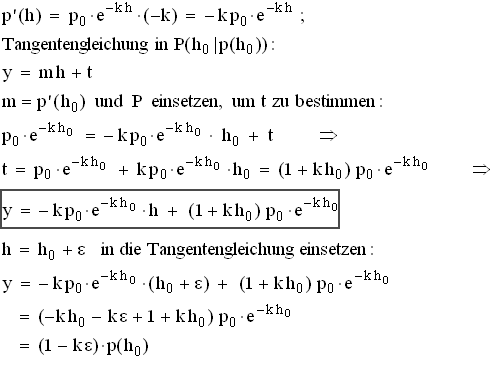 Dieses Ergebnis lässt sich für p(h0+ε) übernehmen,
wenn der Graf von p noch ungefähr mit seiner Tangente in P übereinstimmt,
d. h. für ε ≈ 0.
Dieses Ergebnis lässt sich für p(h0+ε) übernehmen,
wenn der Graf von p noch ungefähr mit seiner Tangente in P übereinstimmt,
d. h. für ε ≈ 0.
1.1Monotonietabelle von f:
| x < | ln 4 | < x | |
| f '(x) | – | 0 | + |
| Graf | fällt | TIP ( ln 4 | 2 – 4 ln 2) | steigt |
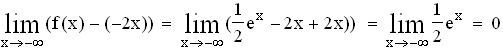 ,
d. h. die Gerade y = –2 x ist für x
,
d. h. die Gerade y = –2 x ist für x  – ∞ Asymptote des Grafen von f
– ∞ Asymptote des Grafen von f  Für x
Für x  – ∞ strebt f(x)
– ∞ strebt f(x)  + ∞.
Für x
+ ∞.
Für x  + ∞ steigt der Graf von f, und f '(x)
+ ∞ steigt der Graf von f, und f '(x)  + ∞
+ ∞  f(x)
f(x)  + ∞.
1.3 Da f für x < ln 4 echt monoton abnimmt und für x > ln 4 echt monoton zunimmt,
hat f genau dann zwei Nullstellen, wenn sein Graf einen Punkt unterhalb der x-Achse
besitzt. Das ist beim Tiefpunkt aber der Fall.
Berechnung einer Nullstelle mit dem Startwert x0 = 0:
+ ∞.
1.3 Da f für x < ln 4 echt monoton abnimmt und für x > ln 4 echt monoton zunimmt,
hat f genau dann zwei Nullstellen, wenn sein Graf einen Punkt unterhalb der x-Achse
besitzt. Das ist beim Tiefpunkt aber der Fall.
Berechnung einer Nullstelle mit dem Startwert x0 = 0:
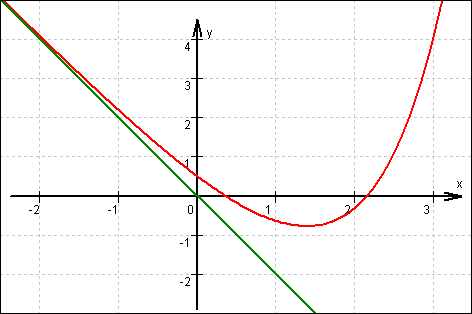
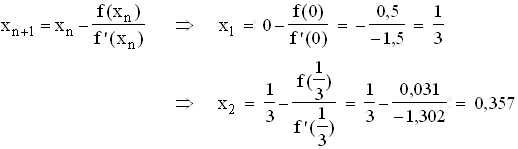 1.4 Graf:
1.4 Graf:
 1.5
1.5 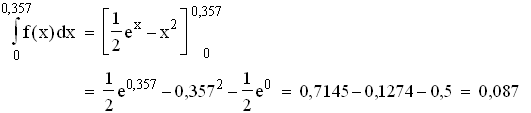 2.1
2.1 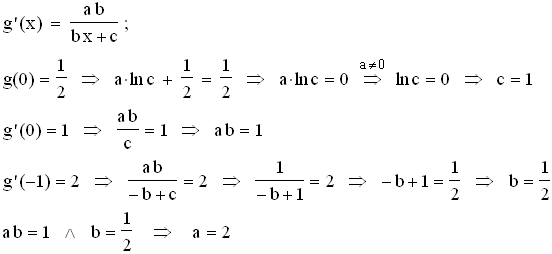 2.2 Bestimmung von IDg: 0,5 x + 1 > 0
2.2 Bestimmung von IDg: 0,5 x + 1 > 0  x > –2, also: IDg = ] –2 ; +∞ [.
x > –2, also: IDg = ] –2 ; +∞ [.
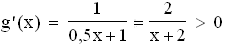 in ID
in ID
 g steigt in ID
g steigt in ID streng monoton.
2.3 f(0) = 0,5
streng monoton.
2.3 f(0) = 0,5 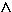 g(0) = 0,5 ln 1 + 0,5 = 0,5
g(0) = 0,5 ln 1 + 0,5 = 0,5  φ ist bei x = 0 stetig.
f fällt für x < 0 und g steigt in seinem ganzen Def.bereich, also auch für x > 0
φ ist bei x = 0 stetig.
f fällt für x < 0 und g steigt in seinem ganzen Def.bereich, also auch für x > 0  φ hat bei x = 0 ein Minimum.
3.1 Im Ansatz D(t) = D
φ hat bei x = 0 ein Minimum.
3.1 Im Ansatz D(t) = D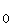
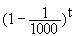 bedeutet D
bedeutet D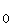 die BRD-Population im Jahre 2001,
D(t) die BRD-Population t Jahre später. Die Basis 0,999 der Potenz drückt aus,
dass die deutsche Bevölkerung pro Jahr um ein Tausendstel abnimmt.
Die Formel ab = eb ln a lautet hier: 0,999t = et ln 0,999 = e–0,0010 t
die BRD-Population im Jahre 2001,
D(t) die BRD-Population t Jahre später. Die Basis 0,999 der Potenz drückt aus,
dass die deutsche Bevölkerung pro Jahr um ein Tausendstel abnimmt.
Die Formel ab = eb ln a lautet hier: 0,999t = et ln 0,999 = e–0,0010 t  D(t) = D
D(t) = D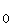
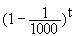 =
= 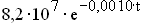 Für die Kongo-Population gilt:
Für die Kongo-Population gilt:
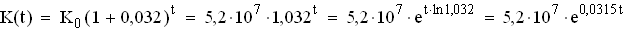 3.2
3.2 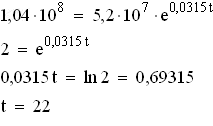 Die Bevölkerung des Kongo wird sich 22 Jahre später, also im Jahre 2023 verdoppelt haben.
Die Bevölkerung des Kongo wird sich 22 Jahre später, also im Jahre 2023 verdoppelt haben.
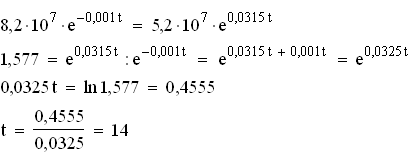 Im Jahre 2015 werden die Einwohnerzahlen von Deutschland und Kongo gleich groß sein.
Im Jahre 2015 werden die Einwohnerzahlen von Deutschland und Kongo gleich groß sein.