Abschlussprüfung zur Erlangung der fachgebundenen Hochschulreife
Frühjahr 2001
B I: Lösungen
1.1 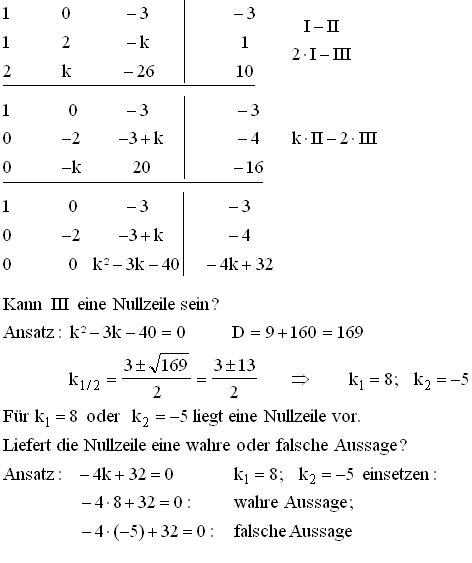
 Für k
Für k 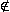 {8 ; –5} gilt:
Rang der Koeffizientenmatrix = Rang der erweiterten Matrix = 3,
d. h. das LGS ist eindeutig lösbar.
Für k = 8 gilt:
Rang der Koeffizientenmatrix = Rang der erweiterten Matrix = 2,
d. h. das LGS hat unendlich viele Lösungen.
Für k = –5 gilt:
Rang der Koeffizientenmatrix = 2, aber Rang der erweiterten Matrix = 3,
d. h. das LGS ist nicht lösbar.
Lösungsmenge für k = 8:
k = 8 in II: –2x2 + 5x3 = –4
{8 ; –5} gilt:
Rang der Koeffizientenmatrix = Rang der erweiterten Matrix = 3,
d. h. das LGS ist eindeutig lösbar.
Für k = 8 gilt:
Rang der Koeffizientenmatrix = Rang der erweiterten Matrix = 2,
d. h. das LGS hat unendlich viele Lösungen.
Für k = –5 gilt:
Rang der Koeffizientenmatrix = 2, aber Rang der erweiterten Matrix = 3,
d. h. das LGS ist nicht lösbar.
Lösungsmenge für k = 8:
k = 8 in II: –2x2 + 5x3 = –4  x2 = 2,5x3 + 2
(k und x2 in I:) x1 – 3x3 = –3
x2 = 2,5x3 + 2
(k und x2 in I:) x1 – 3x3 = –3  x1 = 3x3 – 3
x1 = 3x3 – 3
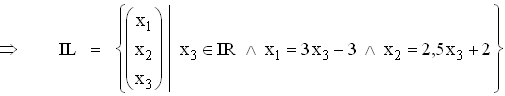 1.2 Für k
1.2 Für k  {8 ; –5} sind die Vektoren der Koeffizientenmatrix linear abhängig,
ansonsten linear unabhängig.
2.1
{8 ; –5} sind die Vektoren der Koeffizientenmatrix linear abhängig,
ansonsten linear unabhängig.
2.1 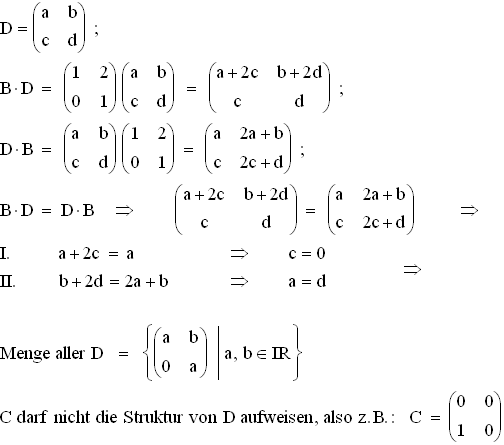 2.2
2.2 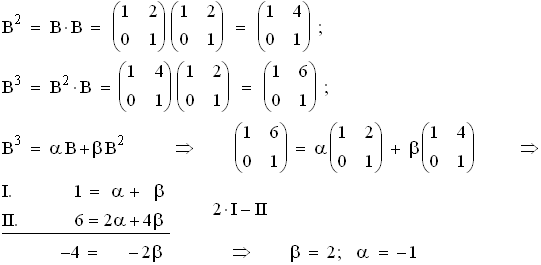 2.3 Vermutung:
2.3 Vermutung:
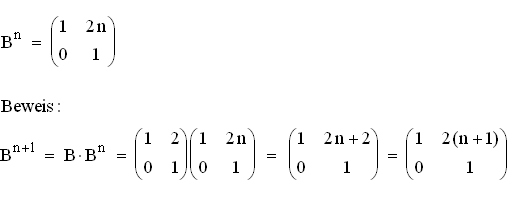 3.1
3.1 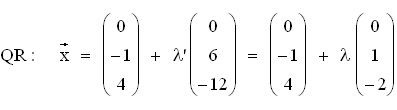
 QR liegt in der x2x3-Koordinatenebene.
x1x3-Koordinatenebene: x2 = 0, also: –1 + λ = 0
QR liegt in der x2x3-Koordinatenebene.
x1x3-Koordinatenebene: x2 = 0, also: –1 + λ = 0  λ = 1 in QR: S (0 | 0 | 2)
3.2 Da beide Geraden parallel sind (Richtungsvektoren sind Gegenvektoren voneinander),
spannen sie genau dann eine Ebene auf, wenn A(3 | 0 | 0)
λ = 1 in QR: S (0 | 0 | 2)
3.2 Da beide Geraden parallel sind (Richtungsvektoren sind Gegenvektoren voneinander),
spannen sie genau dann eine Ebene auf, wenn A(3 | 0 | 0) 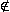 QR:
QR:
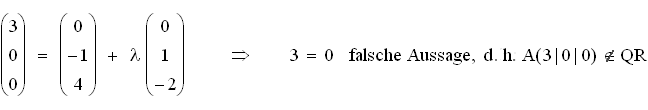 Parametergleichung von E:
Parametergleichung von E: 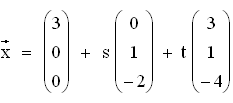 parameterfreie Gleichung von E:
parameterfreie Gleichung von E:
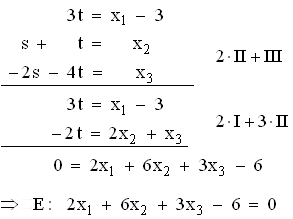 3.3 Das Objekt heiße P. Dann gilt:
3.3 Das Objekt heiße P. Dann gilt:
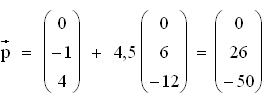
B II: Lösungen
1.1 Die Gerade g und der Punkt Am legen genau dann eine Ebene fest, wenn Am 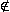 g.
g.
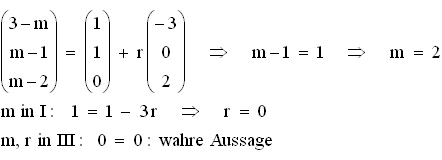 Nur für m = 2 liegt Am auf g, legt also für m ≠2 mit g eine Ebene fest.
1.2 Parametergleichung von E:
Nur für m = 2 liegt Am auf g, legt also für m ≠2 mit g eine Ebene fest.
1.2 Parametergleichung von E: 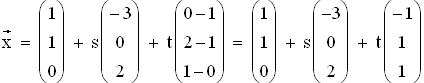 parameterfreie Gleichung von E:
parameterfreie Gleichung von E:
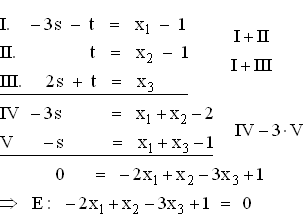 1.3 Die Ebene E halbiert die Strecke [PQa] genau dann, wenn
deren Mittelpunkt M auf E liegt. Bestimmung von M:
1.3 Die Ebene E halbiert die Strecke [PQa] genau dann, wenn
deren Mittelpunkt M auf E liegt. Bestimmung von M:
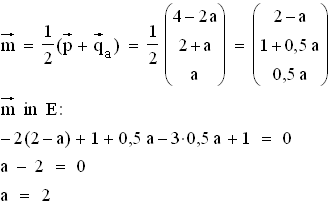 2.1
2.1 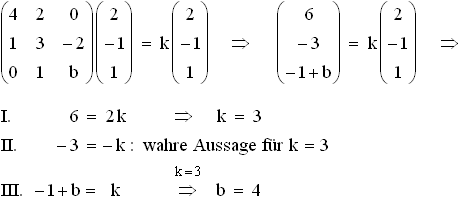 Also ist die Gleichung
Also ist die Gleichung 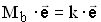 für k = 3 und b = 4 erfüllt.
2.2
für k = 3 und b = 4 erfüllt.
2.2  Für b = –0,8 gilt also:
Rang der Koeffizientenmatrix = 2, aber Rang der erweiterten Matrix = 3.
Für alle anderen b
Für b = –0,8 gilt also:
Rang der Koeffizientenmatrix = 2, aber Rang der erweiterten Matrix = 3.
Für alle anderen b  IR gilt:
Rang der Koeffizientenmatrix = Rang der erweiterten Matrix = 3.
Folglich ist das LGS für b = –0,8 nicht, sonst aber immer eindeutig lösbar.
3.1 Zunächst wird der Produktionsvektor bestimmt und damit dann die Inputmatrix aufgestellt:
IR gilt:
Rang der Koeffizientenmatrix = Rang der erweiterten Matrix = 3.
Folglich ist das LGS für b = –0,8 nicht, sonst aber immer eindeutig lösbar.
3.1 Zunächst wird der Produktionsvektor bestimmt und damit dann die Inputmatrix aufgestellt:
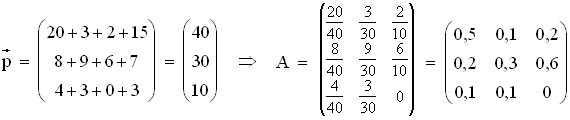 3.2
3.2 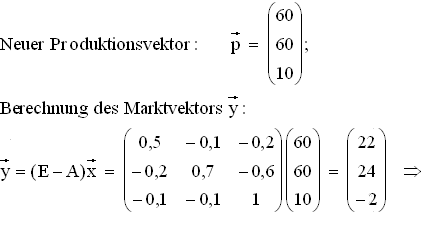 Die Abteilung H müsste 2 Produktionseinheiten vom Markt beziehen,
was nicht möglich ist.
3.3
Die Abteilung H müsste 2 Produktionseinheiten vom Markt beziehen,
was nicht möglich ist.
3.3 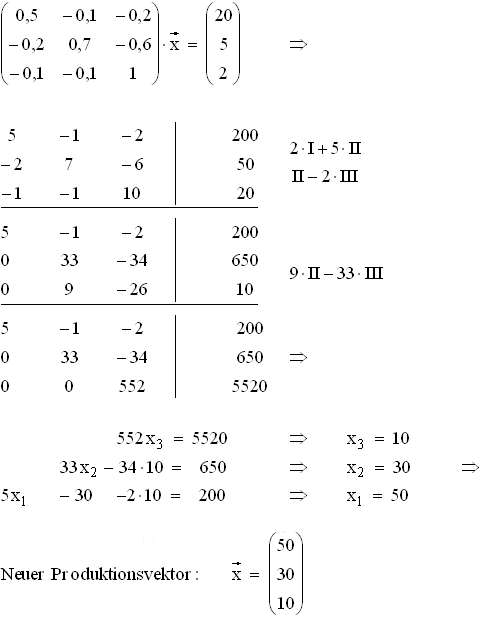 3.4
3.4 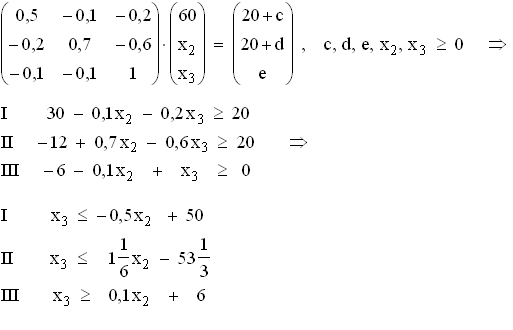 Zunächst werden die in den drei Bedingungen I, II und III enthaltenen
Funktionsgleichungen I', II' und III' mit verschiedenen Farben in einem
x2x3-Diagramm grafisch dargestellt.
Dann wird der durch die Ungleichungen beschriebene Bereich farblich
hervorgehoben:
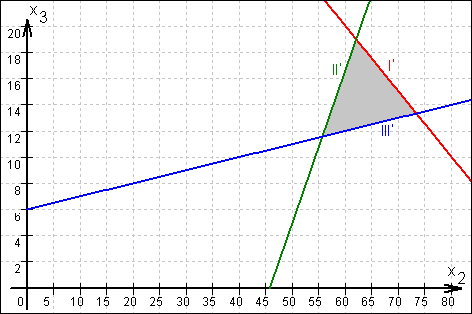
Zunächst werden die in den drei Bedingungen I, II und III enthaltenen
Funktionsgleichungen I', II' und III' mit verschiedenen Farben in einem
x2x3-Diagramm grafisch dargestellt.
Dann wird der durch die Ungleichungen beschriebene Bereich farblich
hervorgehoben:
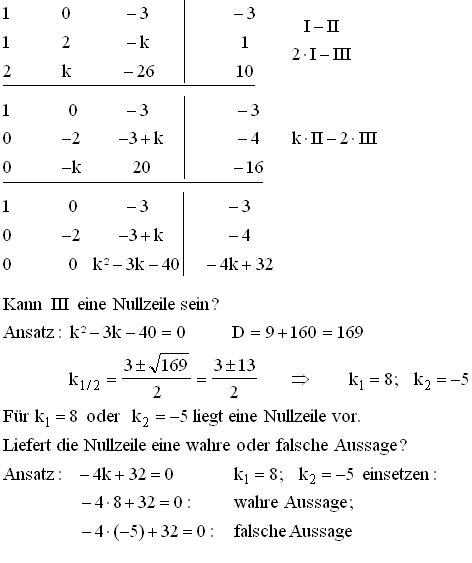
 Für k
Für k 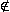 {8 ; –5} gilt:
Rang der Koeffizientenmatrix = Rang der erweiterten Matrix = 3,
d. h. das LGS ist eindeutig lösbar.
Für k = 8 gilt:
Rang der Koeffizientenmatrix = Rang der erweiterten Matrix = 2,
d. h. das LGS hat unendlich viele Lösungen.
Für k = –5 gilt:
Rang der Koeffizientenmatrix = 2, aber Rang der erweiterten Matrix = 3,
d. h. das LGS ist nicht lösbar.
Lösungsmenge für k = 8:
k = 8 in II: –2x2 + 5x3 = –4
{8 ; –5} gilt:
Rang der Koeffizientenmatrix = Rang der erweiterten Matrix = 3,
d. h. das LGS ist eindeutig lösbar.
Für k = 8 gilt:
Rang der Koeffizientenmatrix = Rang der erweiterten Matrix = 2,
d. h. das LGS hat unendlich viele Lösungen.
Für k = –5 gilt:
Rang der Koeffizientenmatrix = 2, aber Rang der erweiterten Matrix = 3,
d. h. das LGS ist nicht lösbar.
Lösungsmenge für k = 8:
k = 8 in II: –2x2 + 5x3 = –4  x2 = 2,5x3 + 2
(k und x2 in I:) x1 – 3x3 = –3
x2 = 2,5x3 + 2
(k und x2 in I:) x1 – 3x3 = –3  x1 = 3x3 – 3
x1 = 3x3 – 3
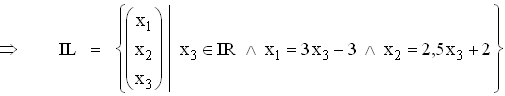 1.2 Für k
1.2 Für k  {8 ; –5} sind die Vektoren der Koeffizientenmatrix linear abhängig,
ansonsten linear unabhängig.
2.1
{8 ; –5} sind die Vektoren der Koeffizientenmatrix linear abhängig,
ansonsten linear unabhängig.
2.1 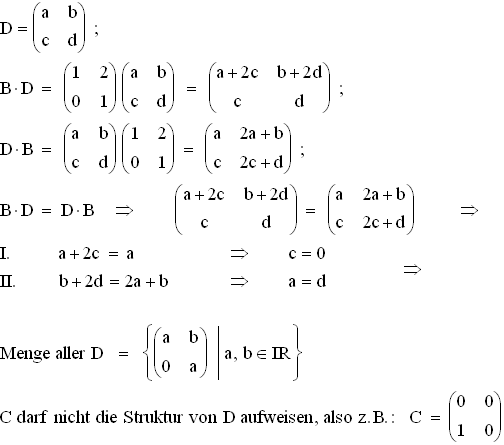 2.2
2.2 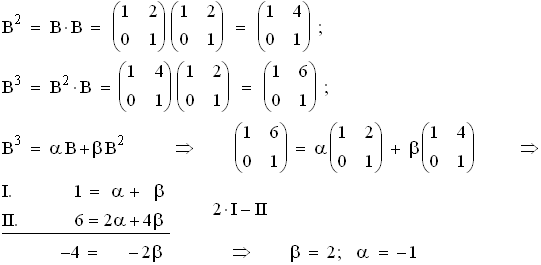 2.3 Vermutung:
2.3 Vermutung:
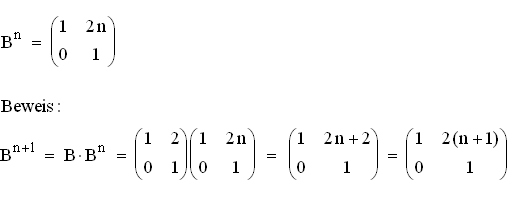 3.1
3.1 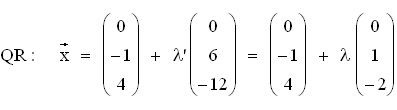
 QR liegt in der x2x3-Koordinatenebene.
x1x3-Koordinatenebene: x2 = 0, also: –1 + λ = 0
QR liegt in der x2x3-Koordinatenebene.
x1x3-Koordinatenebene: x2 = 0, also: –1 + λ = 0  λ = 1 in QR: S (0 | 0 | 2)
3.2 Da beide Geraden parallel sind (Richtungsvektoren sind Gegenvektoren voneinander),
spannen sie genau dann eine Ebene auf, wenn A(3 | 0 | 0)
λ = 1 in QR: S (0 | 0 | 2)
3.2 Da beide Geraden parallel sind (Richtungsvektoren sind Gegenvektoren voneinander),
spannen sie genau dann eine Ebene auf, wenn A(3 | 0 | 0) 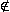 QR:
QR:
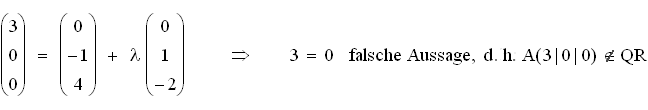 Parametergleichung von E:
Parametergleichung von E: 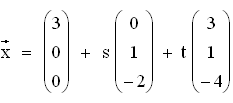 parameterfreie Gleichung von E:
parameterfreie Gleichung von E:
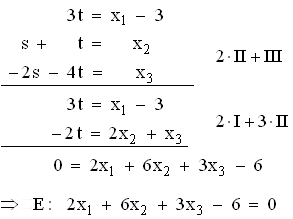 3.3 Das Objekt heiße P. Dann gilt:
3.3 Das Objekt heiße P. Dann gilt:
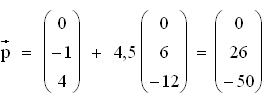
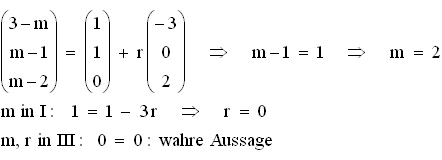 Nur für m = 2 liegt Am auf g, legt also für m ≠2 mit g eine Ebene fest.
1.2 Parametergleichung von E:
Nur für m = 2 liegt Am auf g, legt also für m ≠2 mit g eine Ebene fest.
1.2 Parametergleichung von E: 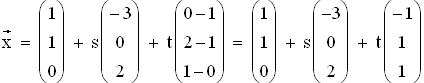 parameterfreie Gleichung von E:
parameterfreie Gleichung von E:
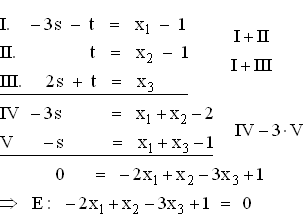 1.3 Die Ebene E halbiert die Strecke [PQa] genau dann, wenn
deren Mittelpunkt M auf E liegt. Bestimmung von M:
1.3 Die Ebene E halbiert die Strecke [PQa] genau dann, wenn
deren Mittelpunkt M auf E liegt. Bestimmung von M:
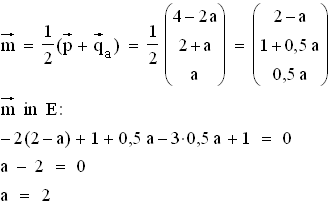 2.1
2.1 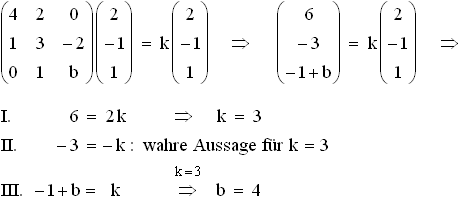 Also ist die Gleichung
Also ist die Gleichung 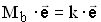 für k = 3 und b = 4 erfüllt.
2.2
für k = 3 und b = 4 erfüllt.
2.2  Für b = –0,8 gilt also:
Rang der Koeffizientenmatrix = 2, aber Rang der erweiterten Matrix = 3.
Für alle anderen b
Für b = –0,8 gilt also:
Rang der Koeffizientenmatrix = 2, aber Rang der erweiterten Matrix = 3.
Für alle anderen b 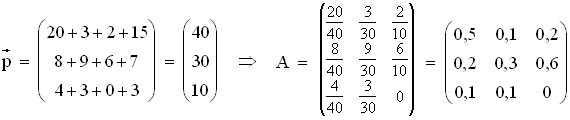 3.2
3.2 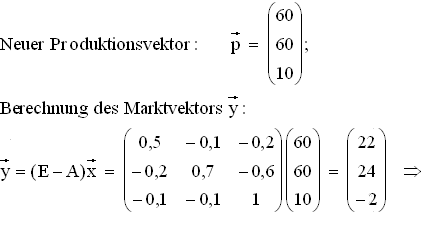 Die Abteilung H müsste 2 Produktionseinheiten vom Markt beziehen,
was nicht möglich ist.
3.3
Die Abteilung H müsste 2 Produktionseinheiten vom Markt beziehen,
was nicht möglich ist.
3.3 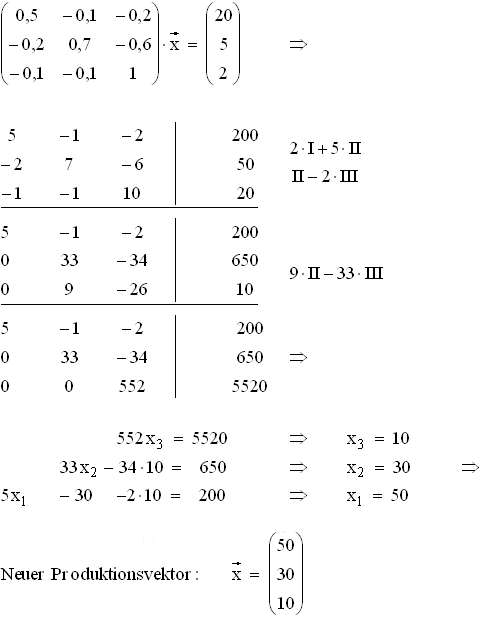 3.4
3.4 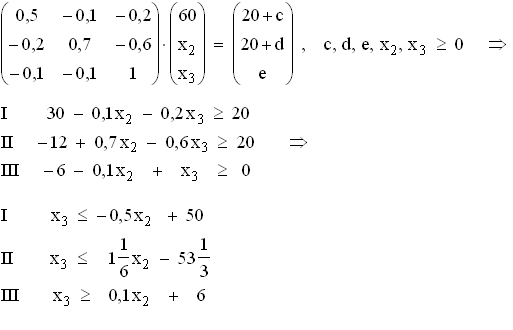 Zunächst werden die in den drei Bedingungen I, II und III enthaltenen
Funktionsgleichungen I', II' und III' mit verschiedenen Farben in einem
x2x3-Diagramm grafisch dargestellt.
Dann wird der durch die Ungleichungen beschriebene Bereich farblich
hervorgehoben:
Zunächst werden die in den drei Bedingungen I, II und III enthaltenen
Funktionsgleichungen I', II' und III' mit verschiedenen Farben in einem
x2x3-Diagramm grafisch dargestellt.
Dann wird der durch die Ungleichungen beschriebene Bereich farblich
hervorgehoben:
