 1.2
1.2 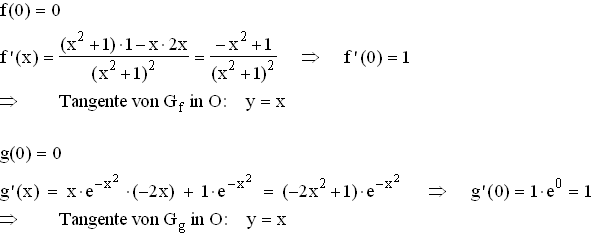 1.3 Nullstellen von f ': –x2 + 1 = 0
1.3 Nullstellen von f ': –x2 + 1 = 0  x2 = 1
x2 = 1  x1 / 2 = ± 1
Monotonieverhalten von f:
x1 / 2 = ± 1
Monotonieverhalten von f:Abschlussprüfung zur Erlangung der fachgebundenen Hochschulreife
Frühjahr 2002
A I: Lösungen
1.11.2
1.3 Nullstellen von f ': –x2 + 1 = 0
x2 = 1
x1 / 2 = ± 1 Monotonieverhalten von f:
| x < | –1 | < x < | 1 | < x | |
|---|---|---|---|---|---|
| Zähler der Ableitungsfkt. | – | 0 | + | 0 | – |
| Nenner der Ableitungsfkt. | + | + | + | + | + |
| Steigung | – | 0 | + | 0 | – |
| Graph | fällt | TIP | steigt | HOP | fällt |
Nullstellen von g ': –2x+ 1 = 0
2x
= 1
x
= ±
≈ ± 0,707 Monotonieverhalten von g:
| x < | – 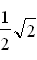 | < x < | 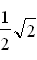 | < x | |
|---|---|---|---|---|---|
| quadr. Faktor der Ableitungsfkt. | – | 0 | + | 0 | – |
| exp. Faktor der Ableitungsfkt. | + | + | + | + | + |
| Steigung | – | 0 | + | 0 | – |
| Graph | fällt | TIP | steigt | HOP | fällt |
1.4Wäre f(x0) für x0
] 0 ; ∞ [ kleiner als g(x0), so müsste h(x0) < 1 gelten, so dass h im Intervall ] 0 ; x0 [ irgendwann fallen müsste, um vom Wert 1 auf einen Wert < 1 zu kommen. Das ist aber nicht möglich, da h in ] 0 ; ∞ [ streng monoton steigt. 1.5
1.6
2.1 Die Funktion k2 ist die Umkehrfunktion der Funktion k1. Also ist die Gerade y = x die Symmetrieachse ihrer Grafen. Da der Graf von k3 auf dieser Geraden senkrecht steht, ist auch er zu ihr symmetrisch. Also muss auch die schraffierte Fläche die Symmetrieachse y = x besitzen. 2.2 Q besitzt genau dann die Abszisse 1, wenn der Schnittansatz ex = –x + (e + 1) die Lösung 1 hat: e1 = –1 + e + 1 ist eine wahre Aussage! Q(1 | e)
R(e | 1) wegen der Achsensymmetrie zu y = x. Berechnungsplan für die schraffierte Fläche A: A = Fläche des Dreiecks, das der Graf von k3 mit den Achsen einschließt – 2 · Restfläche zwischen den Grafen von k3 und k1 im I. Quadranten

A II: Lösungen
1.11.2 Für das Verhalten von f(x) für x
± 1 reicht die Untersuchung des Bruchterms:
| x < | –1 | < x < | 0 | < x < | 1 | < x | |
|---|---|---|---|---|---|---|---|
| 3x | – | – | – | 0 | + | + | + |
| x2–1 | + | 0 | – | – | – | 0 | + |
| f(x) | –  | –∞ / +∞ | 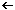 + + | 0 | –  | –∞ / +∞ |  + + |
zwei senkrechte Asymptoten: x = ± 1 Außerdem geht aus der zerlegten Form von f hervor, dass Gf die schiefe Asymptote y = –x besitzt. 1.3
Graf von f und Asymptoten :
1.4
1.5
2.1
Der Wert der Ableitung T '(0) besagt, dass sich die Flüssigkeit in der ersten Sekunde um etwa 0,5 °C abkühlt. Der Grenzwert drückt aus, dass die Flüssigkeit nach längerer Zeit die Umgebungstemperatur von 20 °C annimmt. 2.2
Nach 270 Sekunden hat sich die Flüssigkeit um 55 °C abgekühlt. 3. Wenn für x
–∞ g(x)
1 gilt, dann müssen a = 1 und b·ecx
0 gelten. Da b nicht null sein kann (sonst wäre g(x) = 1, hätte damit keine Nullstelle und schnitte die y-Achse nicht bei y = –3), muss ecx
0 gelten, was für x
–∞ nur für positives c möglich ist. Die Funktion g(x) ist damit auf jeden Fall streng monoton, kommt von y = 1 und schneidet die y-Achse bei y = –3, muss also streng monoton fallen. Das ist nur für ein negatives b möglich, da c > 0. Dann kann sie aber nicht die positive, sondern muss die negative x-Halbachse schneiden, z. B. bei x = –2. Bestimmung von b und c: I. g(0) = –3
1 + b·e0 = –3
b = –4 II. g(–2) = 0
1 – 4·e–2c = 0
e–2c = 0,25
–2c = ln 0,25
c = ln 2.