Abschlussprüfung zur Erlangung der fachgebundenen Hochschulreife
Frühjahr 2002
B I: Lösungen
1.1  1.2 Die vier Ebenen bilden ein LGS von 4 Gleichungen mit 3 Unbekannten.
Lösung mit Hilfe des Gauss-Algorithmus:
1.2 Die vier Ebenen bilden ein LGS von 4 Gleichungen mit 3 Unbekannten.
Lösung mit Hilfe des Gauss-Algorithmus:
 Da die letzte Zeile eine wahre Aussage liefert und die anderen Zeilen den Rang 3 haben,
ist das LGS eindeutig lösbar, d. h. die vier Ebenen haben genau einen Punkt gemeinsam.
III
Da die letzte Zeile eine wahre Aussage liefert und die anderen Zeilen den Rang 3 haben,
ist das LGS eindeutig lösbar, d. h. die vier Ebenen haben genau einen Punkt gemeinsam.
III  x3 = 48
in II
x3 = 48
in II  –3x2 + 48 = 0
–3x2 + 48 = 0  x2 = 16
in I
x2 = 16
in I  20x1 + 384 + 336 = 960
20x1 + 384 + 336 = 960  x1 = 12
x1 = 12
 S(12 | 16 | 48)
1.3 Jeder Punkt P(k | 0 | 0) der x1-Achse mit k
S(12 | 16 | 48)
1.3 Jeder Punkt P(k | 0 | 0) der x1-Achse mit k IR liefert mit E1 eine wahre Aussage
IR liefert mit E1 eine wahre Aussage
 x1-Achse
x1-Achse 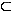 E1.
1.4 A(k | 0 | 0) in E3: 4k = 96
E1.
1.4 A(k | 0 | 0) in E3: 4k = 96  k = 24, also A(24 | 0 | 0)
C(0 | m | 0) in E2: 24m = 960
k = 24, also A(24 | 0 | 0)
C(0 | m | 0) in E2: 24m = 960  m = 40, also C(0 | 40 | 0)
Schnittgerade von E2 und E3:
m = 40, also C(0 | 40 | 0)
Schnittgerade von E2 und E3:
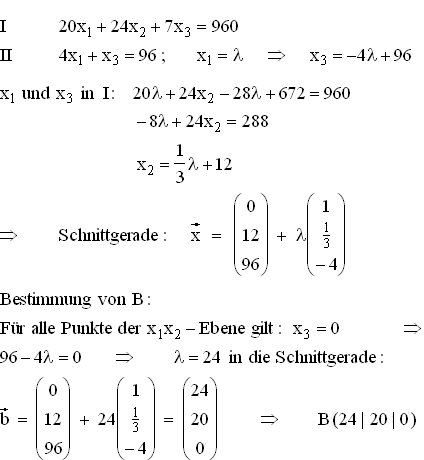 2.1
2.1 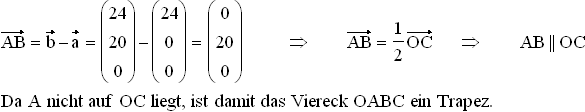 2.2
2.2  2.3
2.3  3.
3. 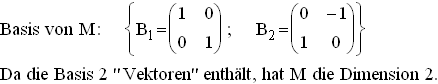
B II: Lösungen
1.1 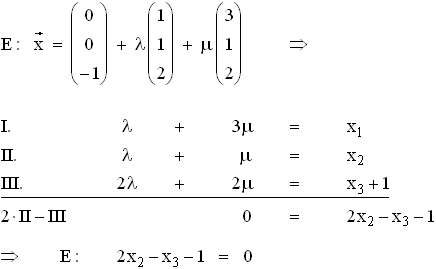 1.2
1.2  Kürzer:
h || E
Kürzer:
h || E 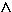 g
g 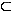 E
E  g und h sind entweder parallel oder windschief.
Richtungsvektoren von g und h nicht parallel
g und h sind entweder parallel oder windschief.
Richtungsvektoren von g und h nicht parallel  g und h sind windschief.
1.3 E liegt parallel zur x1-Achse.
x1x3-Ebene: x2 = 0 in E
g und h sind windschief.
1.3 E liegt parallel zur x1-Achse.
x1x3-Ebene: x2 = 0 in E  x3 = –1 ; x1 beliebig
x3 = –1 ; x1 beliebig  Schnittgerade s :
Schnittgerade s : 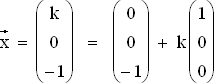 2. In vektorieller Darstellung der Polynome wird angesetzt:
2. In vektorieller Darstellung der Polynome wird angesetzt:
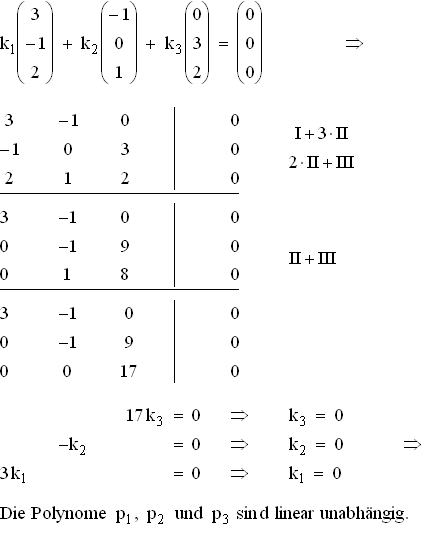 Ein beliebiges Polynom dieses Vektorraumes V hat die Form p = ax2 + bx + c,
ist also durch die drei reellen Parameter a, b und c eindeutig definiert
Ein beliebiges Polynom dieses Vektorraumes V hat die Form p = ax2 + bx + c,
ist also durch die drei reellen Parameter a, b und c eindeutig definiert  dim (V) = 3.
Da in einem Vektorraum der Dimension 3 drei linear unabhängige Vektoren automatisch
eine Basis bilden, gilt dies auch für die gegebenen Polynome bezüglich V.
Koordinaten k1, k2 und k3 des Polynoms p4 bezüglich dieser Basis:
dim (V) = 3.
Da in einem Vektorraum der Dimension 3 drei linear unabhängige Vektoren automatisch
eine Basis bilden, gilt dies auch für die gegebenen Polynome bezüglich V.
Koordinaten k1, k2 und k3 des Polynoms p4 bezüglich dieser Basis:
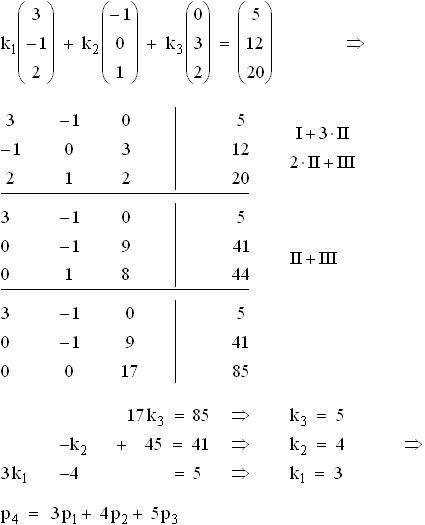 3.1
3.1 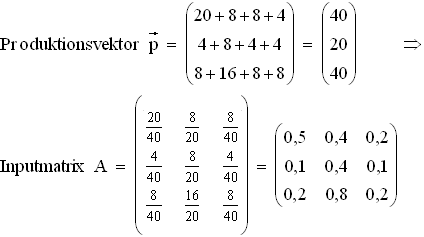 3.2
3.2  3.3
3.3 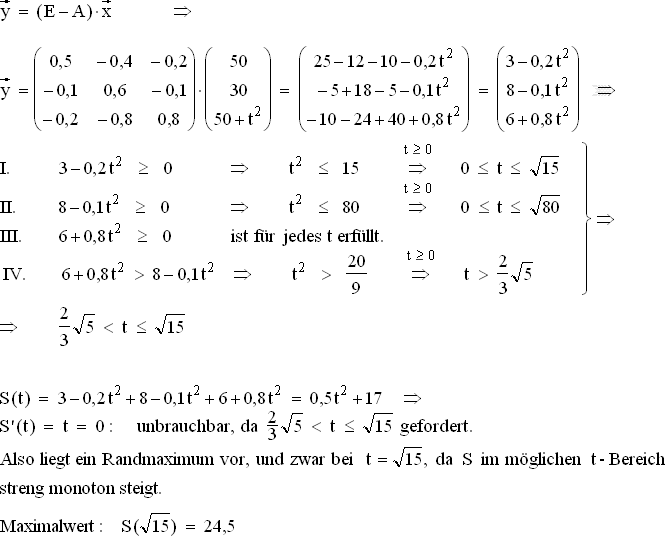
 1.2 Die vier Ebenen bilden ein LGS von 4 Gleichungen mit 3 Unbekannten.
Lösung mit Hilfe des Gauss-Algorithmus:
1.2 Die vier Ebenen bilden ein LGS von 4 Gleichungen mit 3 Unbekannten.
Lösung mit Hilfe des Gauss-Algorithmus:
 Da die letzte Zeile eine wahre Aussage liefert und die anderen Zeilen den Rang 3 haben,
ist das LGS eindeutig lösbar, d. h. die vier Ebenen haben genau einen Punkt gemeinsam.
III
Da die letzte Zeile eine wahre Aussage liefert und die anderen Zeilen den Rang 3 haben,
ist das LGS eindeutig lösbar, d. h. die vier Ebenen haben genau einen Punkt gemeinsam.
III  x3 = 48
in II
x3 = 48
in II  –3x2 + 48 = 0
–3x2 + 48 = 0  x2 = 16
in I
x2 = 16
in I  20x1 + 384 + 336 = 960
20x1 + 384 + 336 = 960  x1 = 12
x1 = 12
 S(12 | 16 | 48)
1.3 Jeder Punkt P(k | 0 | 0) der x1-Achse mit k
S(12 | 16 | 48)
1.3 Jeder Punkt P(k | 0 | 0) der x1-Achse mit k IR liefert mit E1 eine wahre Aussage
IR liefert mit E1 eine wahre Aussage
 x1-Achse
x1-Achse 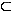 E1.
1.4 A(k | 0 | 0) in E3: 4k = 96
E1.
1.4 A(k | 0 | 0) in E3: 4k = 96  k = 24, also A(24 | 0 | 0)
C(0 | m | 0) in E2: 24m = 960
k = 24, also A(24 | 0 | 0)
C(0 | m | 0) in E2: 24m = 960  m = 40, also C(0 | 40 | 0)
Schnittgerade von E2 und E3:
m = 40, also C(0 | 40 | 0)
Schnittgerade von E2 und E3:
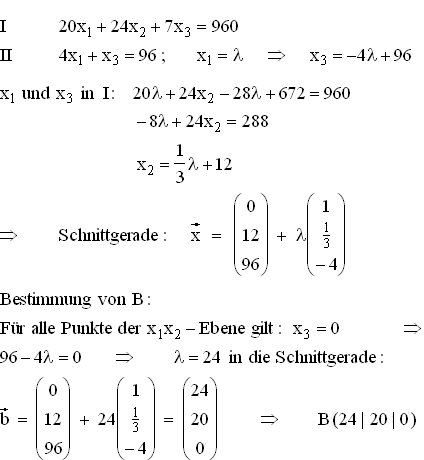 2.1
2.1 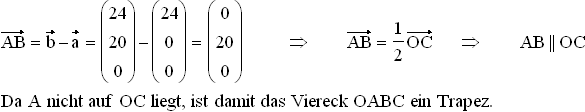 2.2
2.2  2.3
2.3  3.
3. 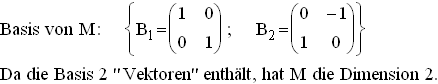
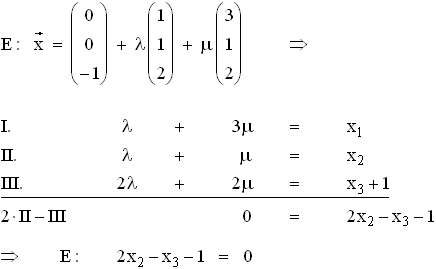 1.2
1.2  Kürzer:
h || E
Kürzer:
h || E 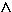 g
g 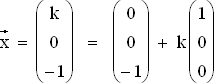 2. In vektorieller Darstellung der Polynome wird angesetzt:
2. In vektorieller Darstellung der Polynome wird angesetzt:
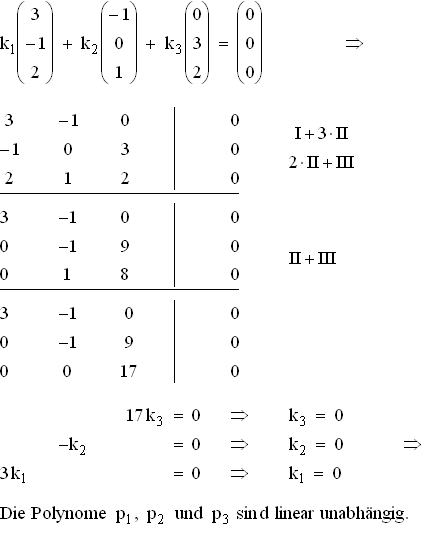 Ein beliebiges Polynom dieses Vektorraumes V hat die Form p = ax2 + bx + c,
ist also durch die drei reellen Parameter a, b und c eindeutig definiert
Ein beliebiges Polynom dieses Vektorraumes V hat die Form p = ax2 + bx + c,
ist also durch die drei reellen Parameter a, b und c eindeutig definiert 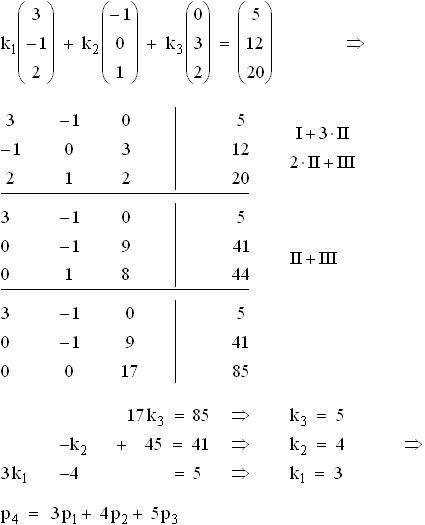 3.1
3.1 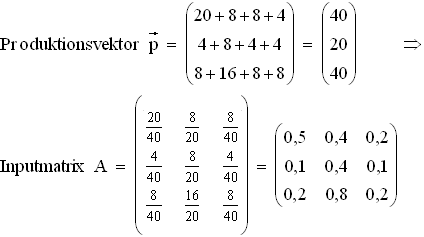 3.2
3.2  3.3
3.3