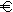Abschlussprüfung zur Erlangung der fachgebundenen Hochschulreife
Frühjahr 2003
A I: Lösungen
1.1 g(–x) = –x (ln ((–x)2) – 2) = –x (ln (x2) – 2) = –g(x)  G(g) ist punktsymmetrisch bzgl. O.
Nullstellen von g :
x (ln (x2) – 2) = 0
G(g) ist punktsymmetrisch bzgl. O.
Nullstellen von g :
x (ln (x2) – 2) = 0  x = 0 ist keine Nullstelle von g, da nicht in der Definitionsmenge von g.
ln (x2) – 2 = 0
x = 0 ist keine Nullstelle von g, da nicht in der Definitionsmenge von g.
ln (x2) – 2 = 0  ln (x2) = 2
ln (x2) = 2  x2 = e2
x2 = e2  x1/2 = ± e .
1.2
x1/2 = ± e .
1.2 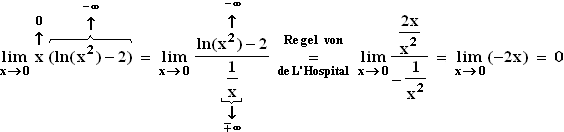
 x = 0 ist eine hebbare Lücke.
1.3
x = 0 ist eine hebbare Lücke.
1.3  1.4 Graf von g :
1.4 Graf von g :
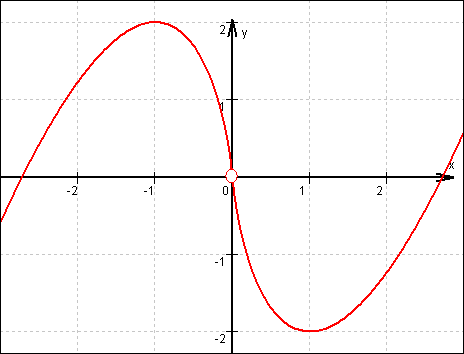 1.5
1.5 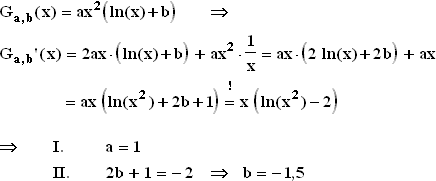 1.6 Es muss also von x = 1 bis zur Nullstelle x = e integriert werden.
Da g(x) in diesem Bereich negativ ist, kommt ein negatives Integral heraus.
Also ist es gleich sinnvoll, die Integrationsgrenzen zu vertauschen :
1.6 Es muss also von x = 1 bis zur Nullstelle x = e integriert werden.
Da g(x) in diesem Bereich negativ ist, kommt ein negatives Integral heraus.
Also ist es gleich sinnvoll, die Integrationsgrenzen zu vertauschen :
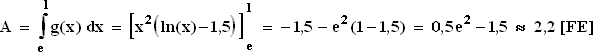 2.1 Nenner = 0
2.1 Nenner = 0 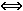 x2 = 9
x2 = 9 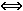 x = ± 3
Also gilt: D(fk) = IR \ {–3; 3}
x = ± 3
Also gilt: D(fk) = IR \ {–3; 3}
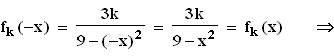 G(fk) ist achsensymmetrisch zur y-Achse.
2.2 Da der Zähler von fk eine positive Konstante ist, hängt das Verhalten von fk
an den Definitionslücken allein vom Nenner ab.
Dieser stellt eine nach unten geöffnete Parabel dar, die bei x = –3 ihr Vorzeichen von
– nach + und bei x = 3 von + nach – wechselt. Also gilt:
G(fk) ist achsensymmetrisch zur y-Achse.
2.2 Da der Zähler von fk eine positive Konstante ist, hängt das Verhalten von fk
an den Definitionslücken allein vom Nenner ab.
Dieser stellt eine nach unten geöffnete Parabel dar, die bei x = –3 ihr Vorzeichen von
– nach + und bei x = 3 von + nach – wechselt. Also gilt:
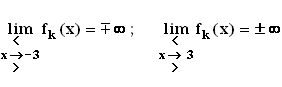 Damit ergeben sich die beiden senkrechten Asymptoten x = –3 und x = 3.
Außerdem muss G(fk) die waagrechte Asymptote y = 0 besitzen, da Zählergrad < Nennergrad.
2.3
Damit ergeben sich die beiden senkrechten Asymptoten x = –3 und x = 3.
Außerdem muss G(fk) die waagrechte Asymptote y = 0 besitzen, da Zählergrad < Nennergrad.
2.3 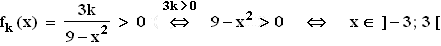 2.4
2.4 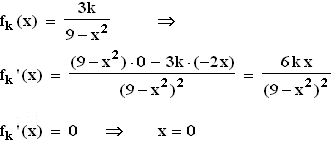 Monotonietabelle:
Monotonietabelle:
| | x < | –3 | < x < | 0 | < x < | 3 | < x |
|---|
| 6kx | – | – | – | 0 | + | + | + |
| (9 – x2)2 | + | 0 | + | + | + | 0 | + |
| f '(x) | – | # | – | 0 | + | # | + |
| G(fk) | fällt | # | fällt | TIP ( 0 | 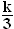 ) ) | steigt | # | steigt |
2.5 Die drei Grafen haben Tiefpunkte mit x = 0 und y = 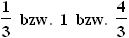 .
Da der y-Wert des TIP von
.
Da der y-Wert des TIP von 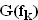 nach Aufgabe 2.4 allgemein
nach Aufgabe 2.4 allgemein 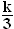 beträgt, muss demnach
k = 1 bzw. 3 bzw. 4 betragen.
3.1
beträgt, muss demnach
k = 1 bzw. 3 bzw. 4 betragen.
3.1 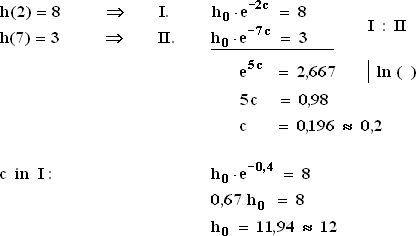 3.2 h0 = 12, d. h. die anfängliche Schaumhöhe betrug 12 cm.
Zum Zeitpunkt t3 beträgt sie also noch 6 cm
3.2 h0 = 12, d. h. die anfängliche Schaumhöhe betrug 12 cm.
Zum Zeitpunkt t3 beträgt sie also noch 6 cm 
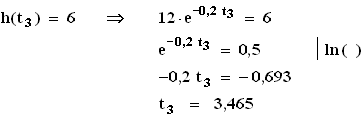 Die Schaumhöhe hat sich nach 3,465 min, also nach 3 Minuten und 28 Sekunden halbiert.
Die Schaumhöhe hat sich nach 3,465 min, also nach 3 Minuten und 28 Sekunden halbiert.
A II: Lösungen
1.1 Nullstelle von f : –4·(x – 1)e0,5 x = 0  x – 1 = 0
x – 1 = 0  x = 1
x = 1
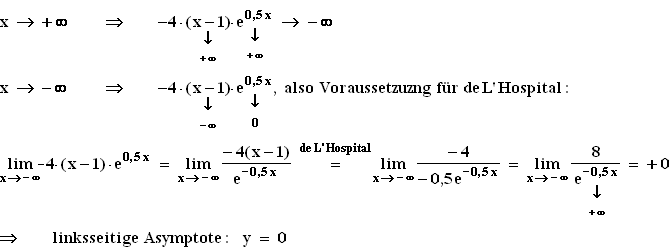 1.2 Maximale Monotonieintervalle von f :
1.2 Maximale Monotonieintervalle von f :
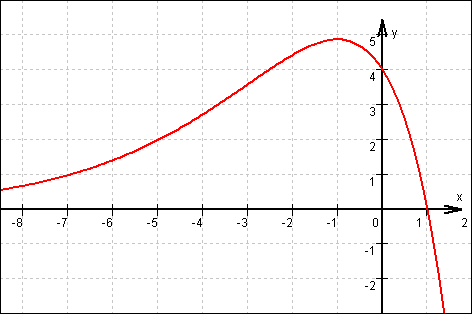
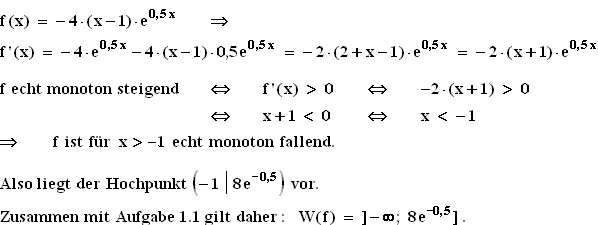 1.3 Graf von f :
1.3 Graf von f :
 1.4.1
1.4.1 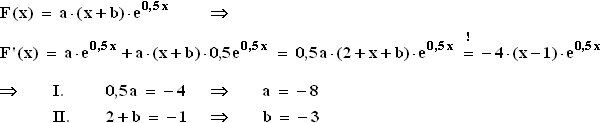 1.4.2
1.4.2 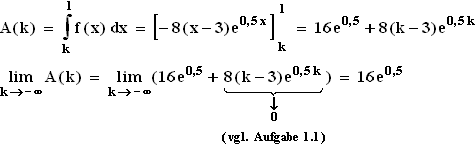 2.1
2.1  2.2
2.2 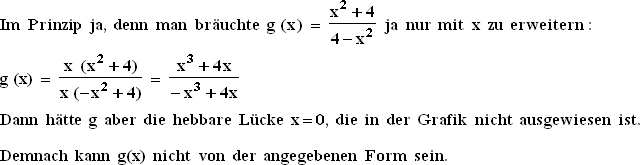 3.1 1,0725 = e ln 1,0725 = e0,07
3.1 1,0725 = e ln 1,0725 = e0,07  K0(1 + 0,0725)t = K0(e0,07)t = K0·e0,07 t
Da K0 den Wert 2000 hat, ergibt sich damit die Behauptung.
3.2 G(t) = 50 · 12 t = 600 t
3.3 Grafen von K und G :
K0(1 + 0,0725)t = K0(e0,07)t = K0·e0,07 t
Da K0 den Wert 2000 hat, ergibt sich damit die Behauptung.
3.2 G(t) = 50 · 12 t = 600 t
3.3 Grafen von K und G :
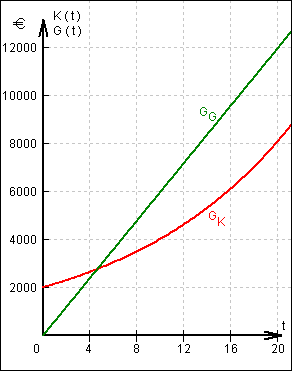 3.4 Es gibt genau zwei Zeitpunkte, zu denen bei beiden Alternativen das gleiche Kapital
angesammelt ist.
Der erste Zeitpunkt ist laut Grafik nach knapp 5 Jahren. Da die Funktion K dann expo-
nenziell immer rascher steigt, die Funktion G aber eine konstante positive Steigung besitzt,
müssen sich beide Grafen für t > 20 noch genau einmal treffen.
Wertetabelle:
3.4 Es gibt genau zwei Zeitpunkte, zu denen bei beiden Alternativen das gleiche Kapital
angesammelt ist.
Der erste Zeitpunkt ist laut Grafik nach knapp 5 Jahren. Da die Funktion K dann expo-
nenziell immer rascher steigt, die Funktion G aber eine konstante positive Steigung besitzt,
müssen sich beide Grafen für t > 20 noch genau einmal treffen.
Wertetabelle:
|
t in Jahren |
4 |
5 |
32 |
33 |
|
K(t) in  |
2646 |
2838 |
18787 |
20149 |
|
G(t) in  |
2400 |
3000 |
19200 |
19800 |
 Zeitintervalle: [4; 5] und [32; 33]
3.5 Langfristig ist die Anlage auf der Bank günstiger, da sie den gesamten Geldbetrag, der bei der
monatlichen Zuwendung anfällt, nach 33 Jahren übersteigt und diesen dann immer weiter hinter
sich lässt.
Andererseits darf der Enkel das auf der Bank liegende Geld etwa eine halbe Lebenszeit lang nicht
anrühren, wenn die Anlageform sich auszahlen soll. Es hängt also letztlich von dessen finanziellen
Bedürfnissen ab, ob er die zukunftsferne „Taube auf dem Dach“ oder den monatlichen „Spatz in der
Hand“ wählt.
Zeitintervalle: [4; 5] und [32; 33]
3.5 Langfristig ist die Anlage auf der Bank günstiger, da sie den gesamten Geldbetrag, der bei der
monatlichen Zuwendung anfällt, nach 33 Jahren übersteigt und diesen dann immer weiter hinter
sich lässt.
Andererseits darf der Enkel das auf der Bank liegende Geld etwa eine halbe Lebenszeit lang nicht
anrühren, wenn die Anlageform sich auszahlen soll. Es hängt also letztlich von dessen finanziellen
Bedürfnissen ab, ob er die zukunftsferne „Taube auf dem Dach“ oder den monatlichen „Spatz in der
Hand“ wählt.
 G(g) ist punktsymmetrisch bzgl. O.
Nullstellen von g :
x (ln (x2) – 2) = 0
G(g) ist punktsymmetrisch bzgl. O.
Nullstellen von g :
x (ln (x2) – 2) = 0  x = 0 ist keine Nullstelle von g, da nicht in der Definitionsmenge von g.
ln (x2) – 2 = 0
x = 0 ist keine Nullstelle von g, da nicht in der Definitionsmenge von g.
ln (x2) – 2 = 0  ln (x2) = 2
ln (x2) = 2  x2 = e2
x2 = e2  x1/2 = ± e .
1.2
x1/2 = ± e .
1.2 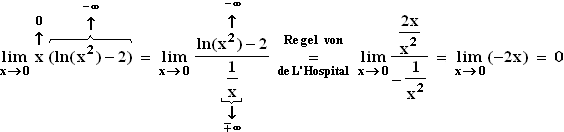
 x = 0 ist eine hebbare Lücke.
1.3
x = 0 ist eine hebbare Lücke.
1.3 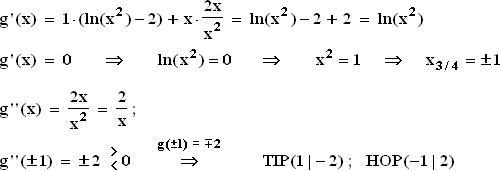 1.4 Graf von g :
1.4 Graf von g :
 1.5
1.5 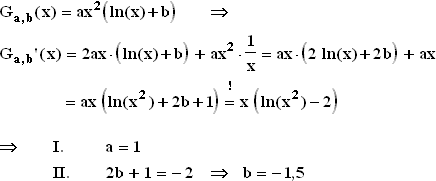 1.6 Es muss also von x = 1 bis zur Nullstelle x = e integriert werden.
Da g(x) in diesem Bereich negativ ist, kommt ein negatives Integral heraus.
Also ist es gleich sinnvoll, die Integrationsgrenzen zu vertauschen :
1.6 Es muss also von x = 1 bis zur Nullstelle x = e integriert werden.
Da g(x) in diesem Bereich negativ ist, kommt ein negatives Integral heraus.
Also ist es gleich sinnvoll, die Integrationsgrenzen zu vertauschen :
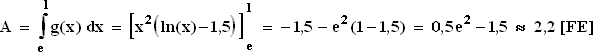 2.1 Nenner = 0
2.1 Nenner = 0 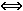 x2 = 9
x2 = 9  x = ± 3
Also gilt: D(fk) = IR \ {–3; 3}
x = ± 3
Also gilt: D(fk) = IR \ {–3; 3}
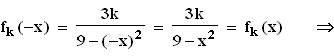 G(fk) ist achsensymmetrisch zur y-Achse.
2.2 Da der Zähler von fk eine positive Konstante ist, hängt das Verhalten von fk
an den Definitionslücken allein vom Nenner ab.
Dieser stellt eine nach unten geöffnete Parabel dar, die bei x = –3 ihr Vorzeichen von
– nach + und bei x = 3 von + nach – wechselt. Also gilt:
G(fk) ist achsensymmetrisch zur y-Achse.
2.2 Da der Zähler von fk eine positive Konstante ist, hängt das Verhalten von fk
an den Definitionslücken allein vom Nenner ab.
Dieser stellt eine nach unten geöffnete Parabel dar, die bei x = –3 ihr Vorzeichen von
– nach + und bei x = 3 von + nach – wechselt. Also gilt:
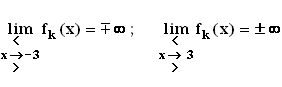 Damit ergeben sich die beiden senkrechten Asymptoten x = –3 und x = 3.
Außerdem muss G(fk) die waagrechte Asymptote y = 0 besitzen, da Zählergrad < Nennergrad.
2.3
Damit ergeben sich die beiden senkrechten Asymptoten x = –3 und x = 3.
Außerdem muss G(fk) die waagrechte Asymptote y = 0 besitzen, da Zählergrad < Nennergrad.
2.3 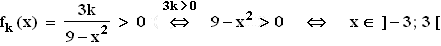 2.4
2.4 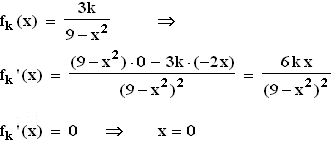 Monotonietabelle:
Monotonietabelle:
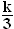 )
)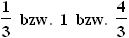 .
Da der y-Wert des TIP von
.
Da der y-Wert des TIP von  nach Aufgabe 2.4 allgemein
nach Aufgabe 2.4 allgemein 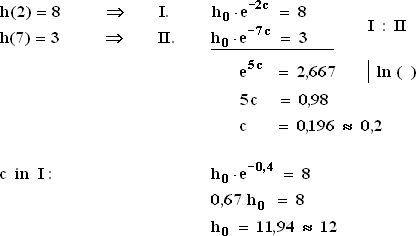
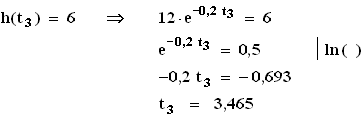 Die Schaumhöhe hat sich nach 3,465 min, also nach 3 Minuten und 28 Sekunden halbiert.
Die Schaumhöhe hat sich nach 3,465 min, also nach 3 Minuten und 28 Sekunden halbiert.
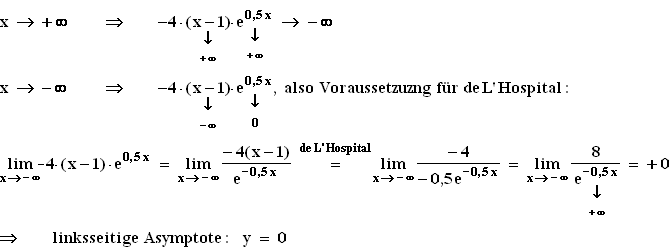 1.2 Maximale Monotonieintervalle von f :
1.2 Maximale Monotonieintervalle von f :
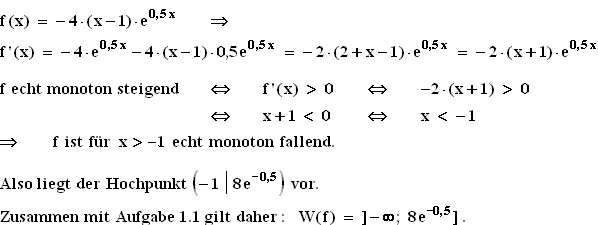 1.3 Graf von f :
1.3 Graf von f :

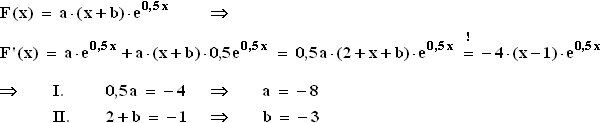
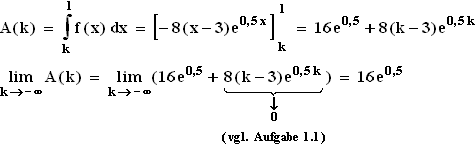

 3.1 1,0725 = e ln 1,0725 = e0,07
3.1 1,0725 = e ln 1,0725 = e0,07  3.4 Es gibt genau zwei Zeitpunkte, zu denen bei beiden Alternativen das gleiche Kapital
angesammelt ist.
Der erste Zeitpunkt ist laut Grafik nach knapp 5 Jahren. Da die Funktion K dann expo-
nenziell immer rascher steigt, die Funktion G aber eine konstante positive Steigung besitzt,
müssen sich beide Grafen für t > 20 noch genau einmal treffen.
Wertetabelle:
3.4 Es gibt genau zwei Zeitpunkte, zu denen bei beiden Alternativen das gleiche Kapital
angesammelt ist.
Der erste Zeitpunkt ist laut Grafik nach knapp 5 Jahren. Da die Funktion K dann expo-
nenziell immer rascher steigt, die Funktion G aber eine konstante positive Steigung besitzt,
müssen sich beide Grafen für t > 20 noch genau einmal treffen.
Wertetabelle: