Abschlussprüfung zur Erlangung der fachgebundenen Hochschulreife
Frühjahr 2003
B I: Lösungen
1.1 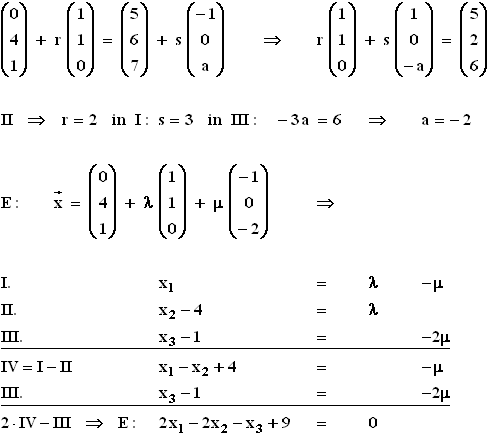 1.2 x2x3-Koordinatenebene: x1 = 0
E: 2x1 – 2x2 – x3 + 9 = 0
x1 = 0; x2 = λ in E : x3 = –2 λ + 9
1.2 x2x3-Koordinatenebene: x1 = 0
E: 2x1 – 2x2 – x3 + 9 = 0
x1 = 0; x2 = λ in E : x3 = –2 λ + 9
 k :
k : 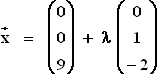 1.3
1.3 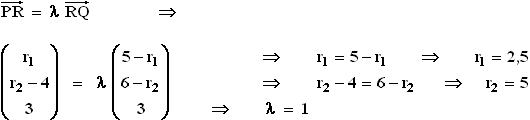 2.1 I. a + 450 + 180 + 10 = 800
2.1 I. a + 450 + 180 + 10 = 800  a = 160
II. b + 360 = 450
a = 160
II. b + 360 = 450  b = 90
III. 160 + c + 80 = 300
b = 90
III. 160 + c + 80 = 300  c = 60
c = 60
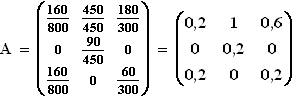 2.2
2.2  2.3
2.3  3.1
3.1 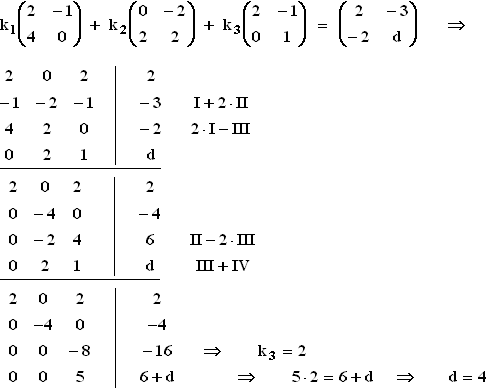 3.2 Nach 3.1 gilt: D = k1A + k2B + k3C
Da E = 3·D, gilt dann E = 3 k1A + 3 k2B + 3 k3C,
so dass A, B, C und E linear abhängig sind.
3.2 Nach 3.1 gilt: D = k1A + k2B + k3C
Da E = 3·D, gilt dann E = 3 k1A + 3 k2B + 3 k3C,
so dass A, B, C und E linear abhängig sind.
B II: Lösungen
1.1 P in g einsetzen:
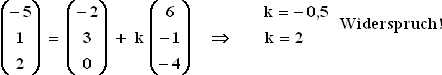
 P
P 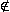 g .
1.2 Parameterform von E1:
g .
1.2 Parameterform von E1:
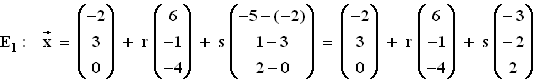 Parameterfreie Form von E1:
Parameterfreie Form von E1:
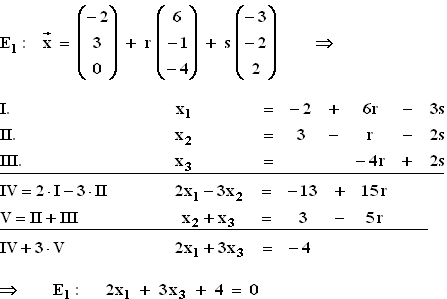 1.3 Es handelt sich um den I. Oktanten. Ein beliebiger Punkt aus diesem Oktanten in die Ebene
E1 eingesetzt ergibt auf der linken Seite einen Wert größer als 4, so dass sich eine Falschaussage
ergibt. Also durchläuft die Ebene E1 diesen Oktanten gar nicht.
Besondere Lage von E1 im Koordinatensystem: x2-Achse || E1
1.3 Es handelt sich um den I. Oktanten. Ein beliebiger Punkt aus diesem Oktanten in die Ebene
E1 eingesetzt ergibt auf der linken Seite einen Wert größer als 4, so dass sich eine Falschaussage
ergibt. Also durchläuft die Ebene E1 diesen Oktanten gar nicht.
Besondere Lage von E1 im Koordinatensystem: x2-Achse || E1 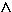 x2-Achse
x2-Achse 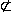 E1
1.4 ha in die parameterfreie Form der Ebene E1 einsetzen :
2 (–5 – 3m) + 3 (2 + a m) + 4 = 0
–10 – 6m + 6 + 3 a m + 4 = 0
(3a – 6) m = 0
E1
1.4 ha in die parameterfreie Form der Ebene E1 einsetzen :
2 (–5 – 3m) + 3 (2 + a m) + 4 = 0
–10 – 6m + 6 + 3 a m + 4 = 0
(3a – 6) m = 0
 Für a ≠ 2 folgt m = 0, d. h. die Gerade ha schneidet die Ebene E1 in ihrem Aufpunkt P;
für a = 2 ergibt sich für jedes m eine wahre Aussage, d. h. die Gerade h2 liegt in E1.
1.5 Für a = 0 und a = 1 ergeben sich zwei verschiedene Richtungsvektoren der Geradenschar.
Deren Differenzvektor muss dann ebenfalls ein Richtungsvektor der Ebene E2 sein.
Für a ≠ 2 folgt m = 0, d. h. die Gerade ha schneidet die Ebene E1 in ihrem Aufpunkt P;
für a = 2 ergibt sich für jedes m eine wahre Aussage, d. h. die Gerade h2 liegt in E1.
1.5 Für a = 0 und a = 1 ergeben sich zwei verschiedene Richtungsvektoren der Geradenschar.
Deren Differenzvektor muss dann ebenfalls ein Richtungsvektor der Ebene E2 sein.
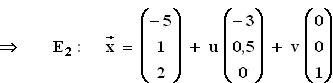 1.6 Nach Aufgabe 1.2 liegt g in E1. Aus Aufgabe 1.4 geht für a ≠ 2 hervor, dass ha die
Ebene E1 im Punkt P schneidet, der nach 1.1 nicht auf g liegt. Demnach müssen g und
ha windschief sein.
2.1
1.6 Nach Aufgabe 1.2 liegt g in E1. Aus Aufgabe 1.4 geht für a ≠ 2 hervor, dass ha die
Ebene E1 im Punkt P schneidet, der nach 1.1 nicht auf g liegt. Demnach müssen g und
ha windschief sein.
2.1 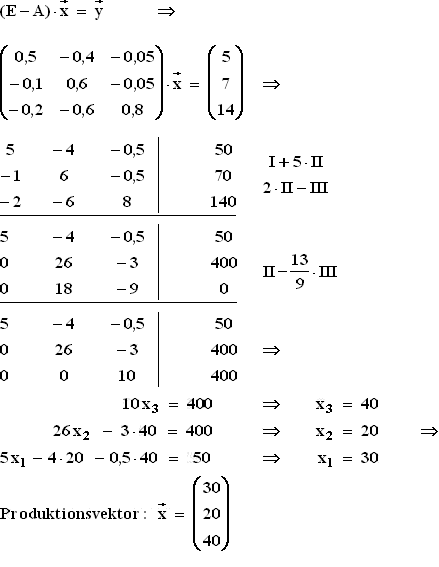 Input-Output-Tabelle :
Input-Output-Tabelle :
| |
U |
V |
W |
Markt |
Produktion |
|
U |
0,5·30 = 15 |
0,4·20 = 8 |
0,05·40 = 2 |
5 |
30 |
|
V |
0,1·30 = 3 |
0,4·20 = 8 |
0,05·40 = 2 |
7 |
20 |
|
W |
0,2·30 = 6 |
0,6·20 = 12 |
0,2·40 = 8 |
14 |
40 |
2.2  3.
3. 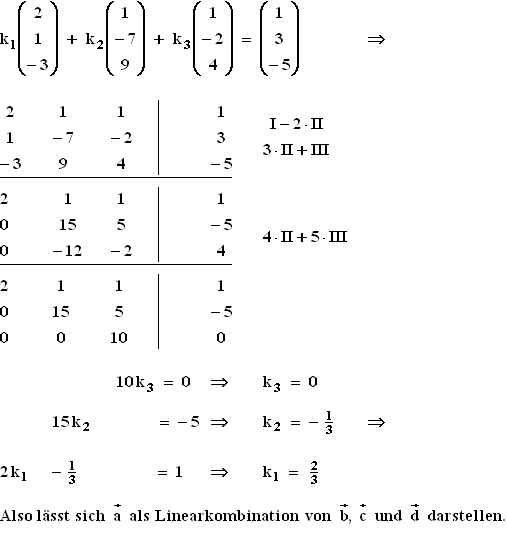
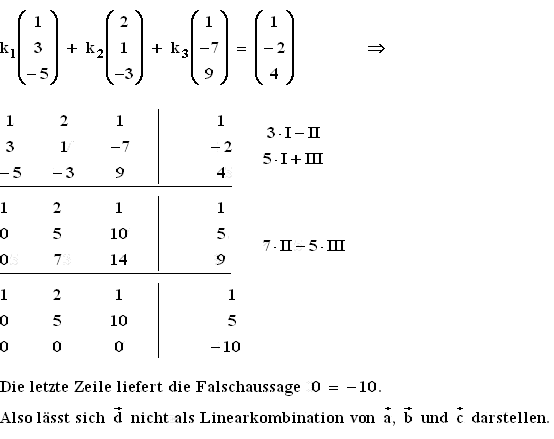 Aus der ersten Rechnung geht hervor, dass
Aus der ersten Rechnung geht hervor, dass  sich nur durch
sich nur durch 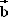 und
und 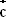 ausdrücken lässt
und
ausdrücken lässt
und 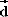 dazu nichts beitragen kann.
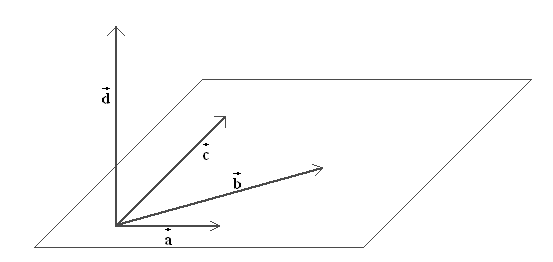
Das bedeutet, dass
dazu nichts beitragen kann.
Das bedeutet, dass  ,
, 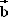 und
und 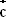 in einer Ebene liegen, in der jedoch nicht
in einer Ebene liegen, in der jedoch nicht 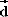 liegt :
liegt :
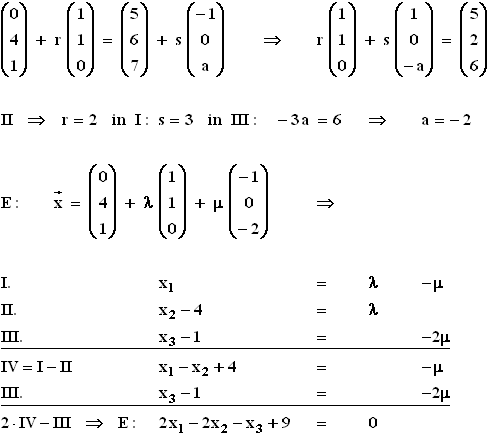 1.2 x2x3-Koordinatenebene: x1 = 0
E: 2x1 – 2x2 – x3 + 9 = 0
x1 = 0; x2 = λ in E : x3 = –2 λ + 9
1.2 x2x3-Koordinatenebene: x1 = 0
E: 2x1 – 2x2 – x3 + 9 = 0
x1 = 0; x2 = λ in E : x3 = –2 λ + 9
 k :
k : 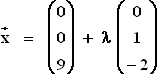 1.3
1.3 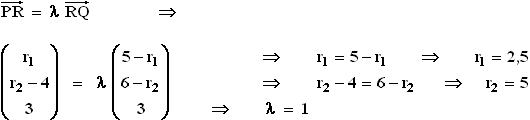 2.1 I. a + 450 + 180 + 10 = 800
2.1 I. a + 450 + 180 + 10 = 800  a = 160
II. b + 360 = 450
a = 160
II. b + 360 = 450  b = 90
III. 160 + c + 80 = 300
b = 90
III. 160 + c + 80 = 300  c = 60
c = 60
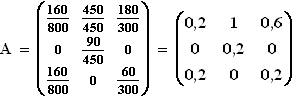 2.2
2.2  2.3
2.3  3.1
3.1 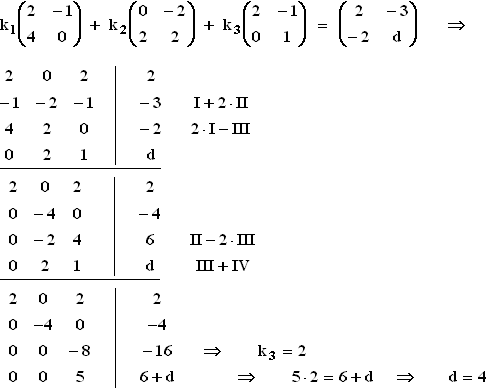 3.2 Nach 3.1 gilt: D = k1A + k2B + k3C
Da E = 3·D, gilt dann E = 3 k1A + 3 k2B + 3 k3C,
so dass A, B, C und E linear abhängig sind.
3.2 Nach 3.1 gilt: D = k1A + k2B + k3C
Da E = 3·D, gilt dann E = 3 k1A + 3 k2B + 3 k3C,
so dass A, B, C und E linear abhängig sind.
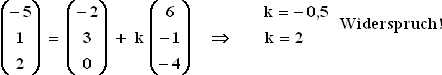
 g .
g .
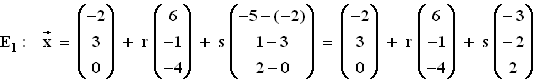 Parameterfreie Form von E1:
Parameterfreie Form von E1:
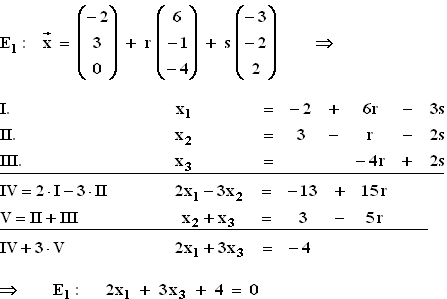
 x2-Achse
x2-Achse  E1
E1
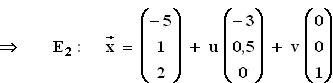
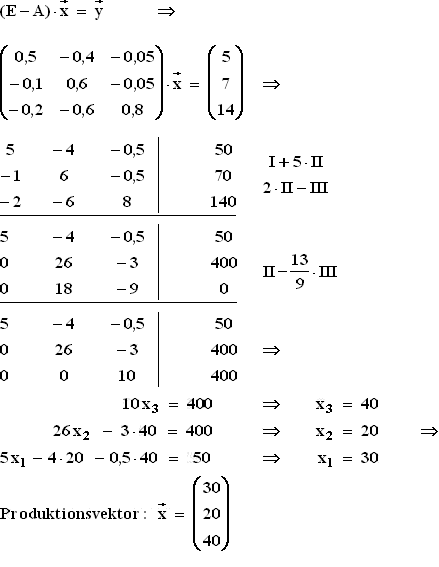 Input-Output-Tabelle :
Input-Output-Tabelle :

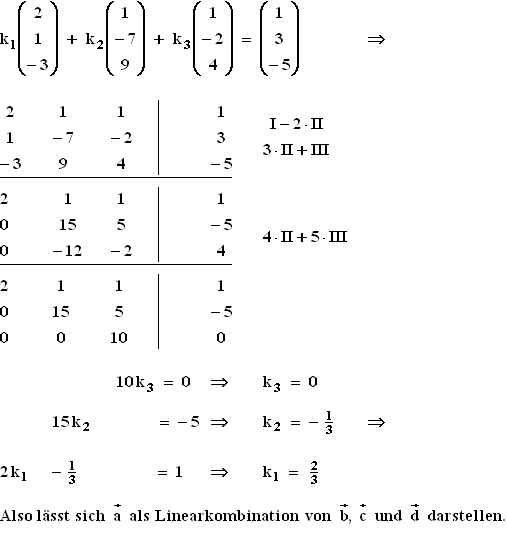
 Aus der ersten Rechnung geht hervor, dass
Aus der ersten Rechnung geht hervor, dass  sich nur durch
sich nur durch 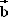 und
und 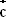 ausdrücken lässt
und
ausdrücken lässt
und 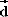 dazu nichts beitragen kann.
Das bedeutet, dass
dazu nichts beitragen kann.
Das bedeutet, dass 