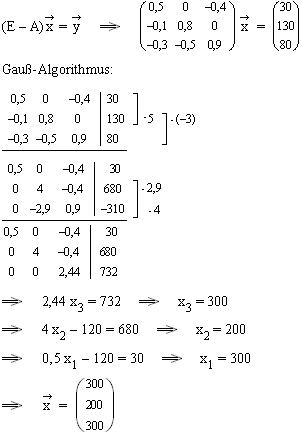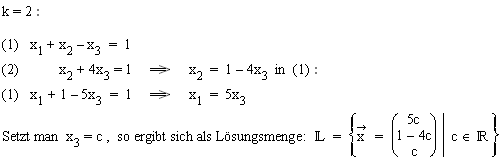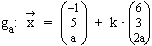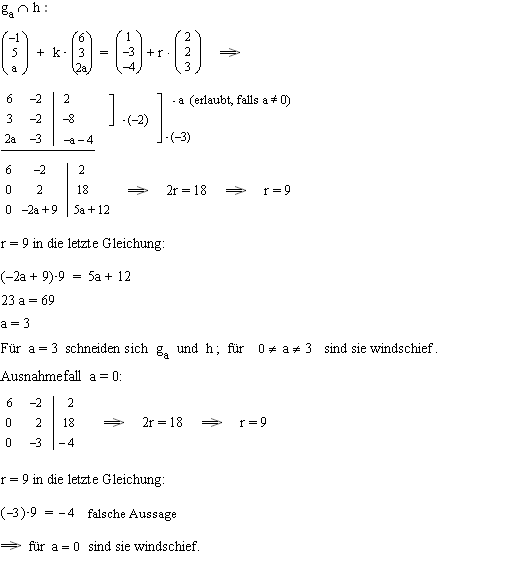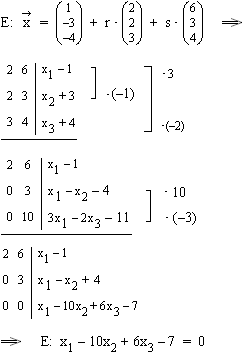Abschlussprüfung zur Erlangung der fachgebundenen Hochschulreife
Frühjahr 2004
B I: Lösungen
1.1 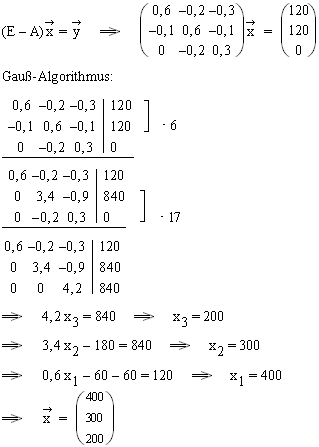 1.2
1.2 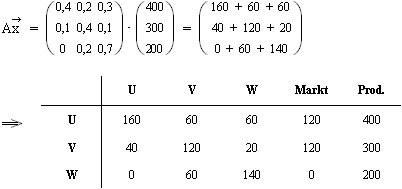 1.3
1.3 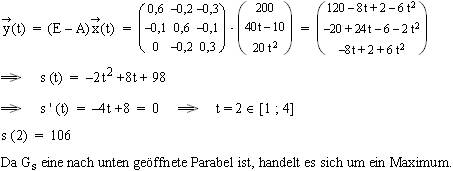 2.1
2.1 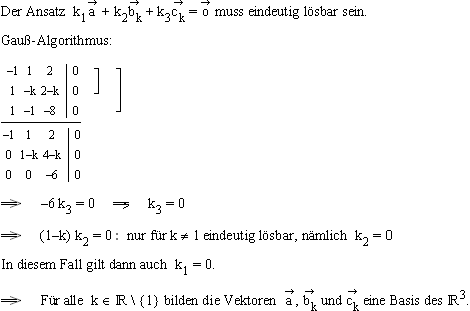 2.2
2.2 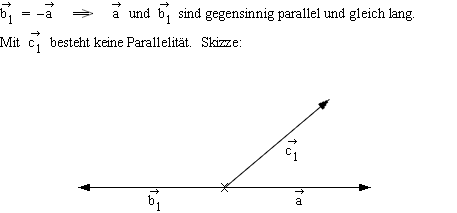 2.3
2.3 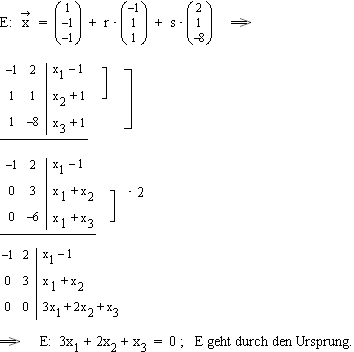 2.4 gm in E:
3(6 + 3t) + 2(5 + 2t) + m·t = 0
(13 + m) t = –28
Für m = –13 ergibt sich eine Falschaussage, so dass in diesem Fall
die Gerade und die Ebene echt parallel sind.
Für alle anderen m-Werte schneiden sich die Gerade und die Ebene
in einem Punkt.
Für m = 1 ergibt sich t = –2.
Dieser t-Wert ergibt mit m = 1 in die Gerade eingesetzt S(0 | 1 | –2).
2.5
2.4 gm in E:
3(6 + 3t) + 2(5 + 2t) + m·t = 0
(13 + m) t = –28
Für m = –13 ergibt sich eine Falschaussage, so dass in diesem Fall
die Gerade und die Ebene echt parallel sind.
Für alle anderen m-Werte schneiden sich die Gerade und die Ebene
in einem Punkt.
Für m = 1 ergibt sich t = –2.
Dieser t-Wert ergibt mit m = 1 in die Gerade eingesetzt S(0 | 1 | –2).
2.5 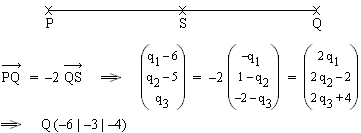
B II: Lösungen
1.1  Den Nullen kann man noch eine zweite Bedeutung beimessen:
Da sie nicht in der Hauptdiagonalen der Matrix E – A stehen,
kommen sie auch in der Inputmatrix A selber vor.
Das heißt dann aber, dass U nichts an V und V nichts an W
liefert.
1.2
Den Nullen kann man noch eine zweite Bedeutung beimessen:
Da sie nicht in der Hauptdiagonalen der Matrix E – A stehen,
kommen sie auch in der Inputmatrix A selber vor.
Das heißt dann aber, dass U nichts an V und V nichts an W
liefert.
1.2 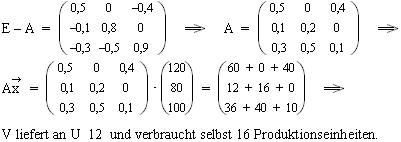 1.3
1.3 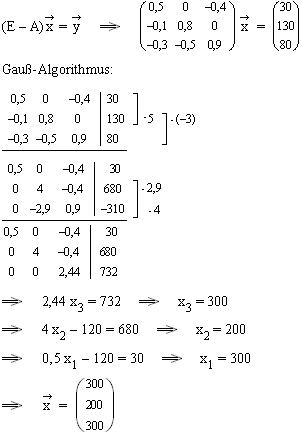 2.1
2.1  2.2
2.2  3.1
3.1  3.2
3.2 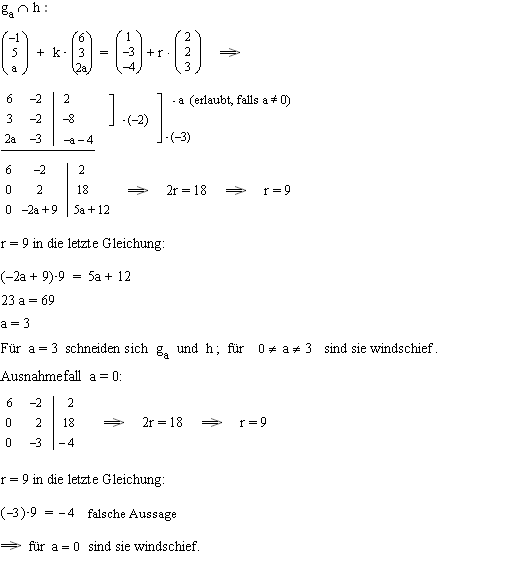 3.3
3.3 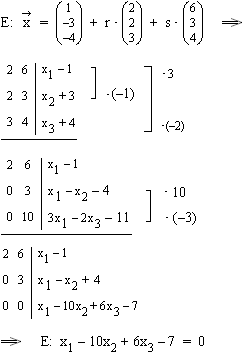 3.4
3.4 
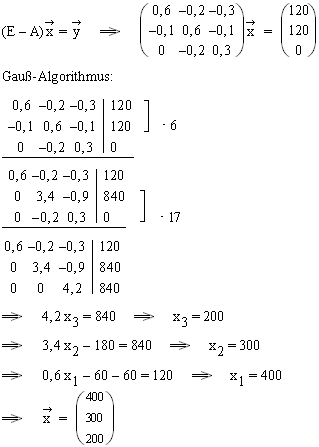 1.2
1.2 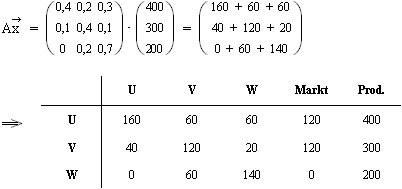 1.3
1.3 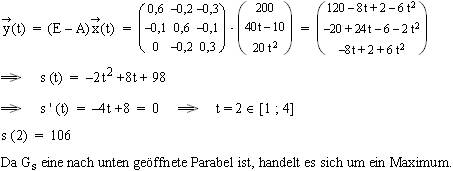 2.1
2.1 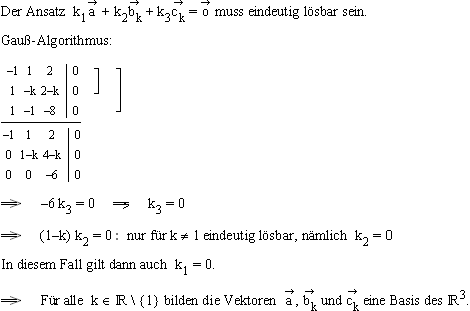 2.2
2.2 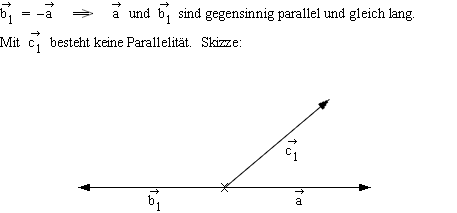 2.3
2.3 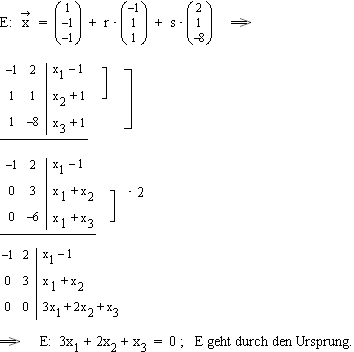 2.4 gm in E:
3(6 + 3t) + 2(5 + 2t) + m·t = 0
(13 + m) t = –28
Für m = –13 ergibt sich eine Falschaussage, so dass in diesem Fall
die Gerade und die Ebene echt parallel sind.
Für alle anderen m-Werte schneiden sich die Gerade und die Ebene
in einem Punkt.
Für m = 1 ergibt sich t = –2.
Dieser t-Wert ergibt mit m = 1 in die Gerade eingesetzt S(0 | 1 | –2).
2.5
2.4 gm in E:
3(6 + 3t) + 2(5 + 2t) + m·t = 0
(13 + m) t = –28
Für m = –13 ergibt sich eine Falschaussage, so dass in diesem Fall
die Gerade und die Ebene echt parallel sind.
Für alle anderen m-Werte schneiden sich die Gerade und die Ebene
in einem Punkt.
Für m = 1 ergibt sich t = –2.
Dieser t-Wert ergibt mit m = 1 in die Gerade eingesetzt S(0 | 1 | –2).
2.5 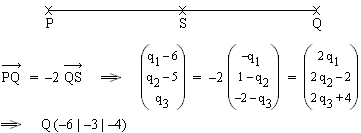
 Den Nullen kann man noch eine zweite Bedeutung beimessen:
Da sie nicht in der Hauptdiagonalen der Matrix E – A stehen,
kommen sie auch in der Inputmatrix A selber vor.
Das heißt dann aber, dass U nichts an V und V nichts an W
liefert.
Den Nullen kann man noch eine zweite Bedeutung beimessen:
Da sie nicht in der Hauptdiagonalen der Matrix E – A stehen,
kommen sie auch in der Inputmatrix A selber vor.
Das heißt dann aber, dass U nichts an V und V nichts an W
liefert.