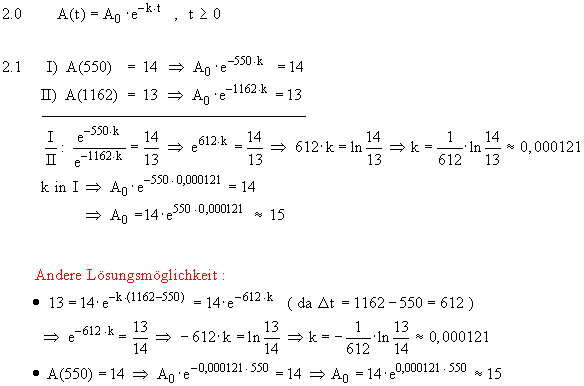Abschlussprüfung zur Erlangung der fachgebundenen
Hochschulreife
Frühjahr 2005
A I: Lösungen
1.1 Der Zähler des Arguments hat die Nullstelle x = 2, der Nenner x = 0.
Vorzeichentabelle des Arguments der Logarithmusfunktion:
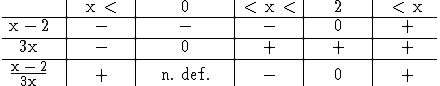 Da der natürliche Logarithmus nur für positive Argumente definiert ist, folgt aus der Tabelle:
D(f) = IR \ [0;2].
Da der natürliche Logarithmus nur für positive Argumente definiert ist, folgt aus der Tabelle:
D(f) = IR \ [0;2].
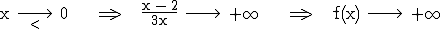
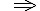 senkr. Asymptote: x = 0
senkr. Asymptote: x = 0
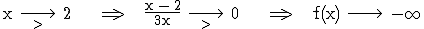
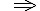 senkr. Asymptote: x = 2
senkr. Asymptote: x = 2
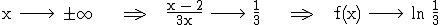
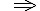 waagr. Asymptote: y =
waagr. Asymptote: y = 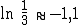 Nullstelle von f:
Nullstelle von f:
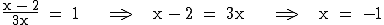 1.2
1.2 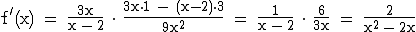 > 0 in D(f)
> 0 in D(f)
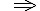 f steigt echt monoton in
f steigt echt monoton in 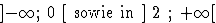 .
1.3
.
1.3 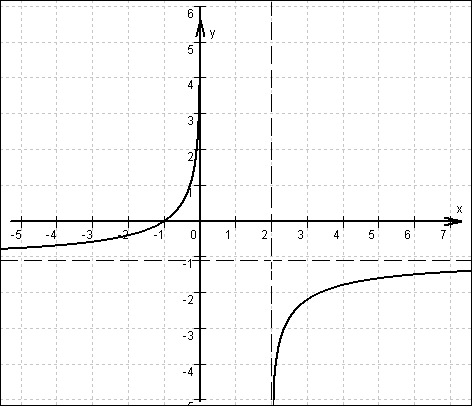 1.4 F '(x) = f(x) = 0
1.4 F '(x) = f(x) = 0 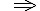 x = –1
f wechselt bei x = –1 von – nach +
x = –1
f wechselt bei x = –1 von – nach +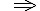 F hat bei x = –1 einen Tiefpunkt.
F ''(x) = f '(x) > 0 in D(F)
F hat bei x = –1 einen Tiefpunkt.
F ''(x) = f '(x) > 0 in D(F) 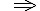 Der Graph von F ist in ganz D(F) linksgekrümmt.
2.1 2x – 4 = 0
Der Graph von F ist in ganz D(F) linksgekrümmt.
2.1 2x – 4 = 0 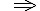 x = 2
x = 2 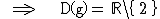 Der Nenner wechselt bei x = 2 von – nach + und der Zähler ist dort positiv. Also gilt:
Der Nenner wechselt bei x = 2 von – nach + und der Zähler ist dort positiv. Also gilt:
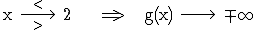 Folglich ist x = 2 eine senkrechte Asymptote.
Da der Zählergrad von g um 1 größer ist als der Nennergrad, gibt es außerdem eine schiefe
Asymptote, deren Gleichung durch Polynomdivision ermittelt wird:
Folglich ist x = 2 eine senkrechte Asymptote.
Da der Zählergrad von g um 1 größer ist als der Nennergrad, gibt es außerdem eine schiefe
Asymptote, deren Gleichung durch Polynomdivision ermittelt wird:
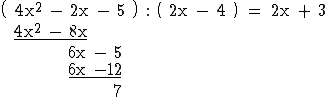 Also lautet die Gleichung der schiefen Asymptote y = 2x + 3.
2.2 Der Graph von g verläuft genau dann oberhalb seiner schiefen Asymptote y = 2x + 3, wenn
der echt-gebrochen-rationale Anteil von g positiv ist:
Also lautet die Gleichung der schiefen Asymptote y = 2x + 3.
2.2 Der Graph von g verläuft genau dann oberhalb seiner schiefen Asymptote y = 2x + 3, wenn
der echt-gebrochen-rationale Anteil von g positiv ist:
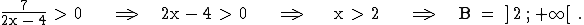 2.3
2.3 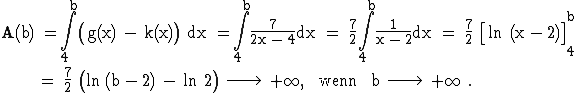 3.1 p(0) =
3.1 p(0) = 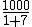 = 125 ;
= 125 ; 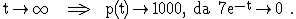
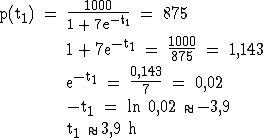 3.2
3.2 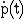 gibt das momentane Wachstum der Anzahl der Pilze zum Zeitpunkt t an.
gibt das momentane Wachstum der Anzahl der Pilze zum Zeitpunkt t an.
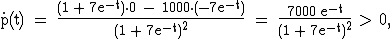 da Zähler und Nenner positiv sind.
Also nimmt die Anzahl der Pilze im gesamten Beobachtungszeitraum echt monoton zu.
3.3
3.4
da Zähler und Nenner positiv sind.
Also nimmt die Anzahl der Pilze im gesamten Beobachtungszeitraum echt monoton zu.
3.3
3.4 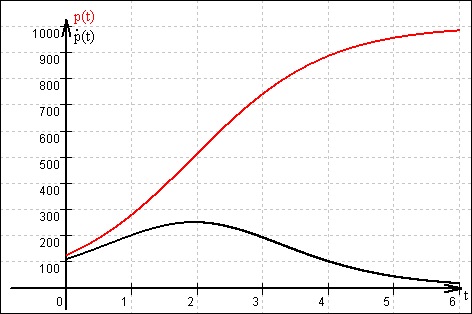
A II: Lösungen


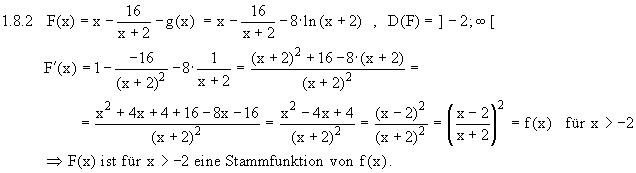
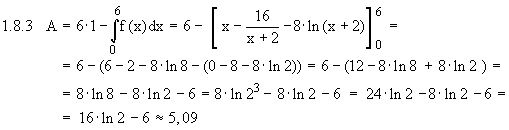
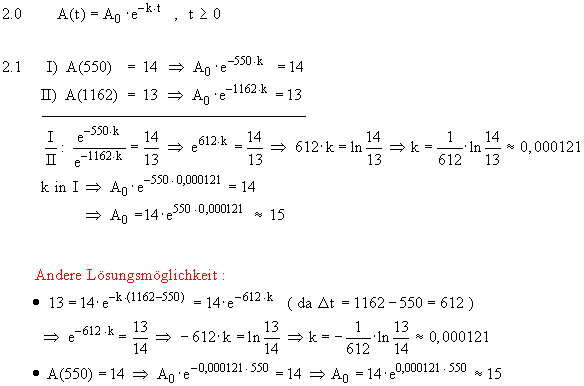

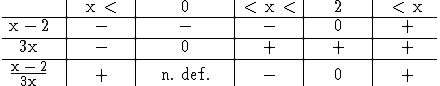 Da der natürliche Logarithmus nur für positive Argumente definiert ist, folgt aus der Tabelle:
D(f) = IR \ [0;2].
Da der natürliche Logarithmus nur für positive Argumente definiert ist, folgt aus der Tabelle:
D(f) = IR \ [0;2].
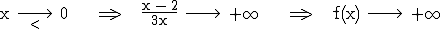
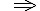 senkr. Asymptote: x = 0
senkr. Asymptote: x = 0
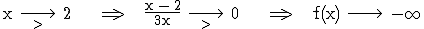
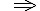 senkr. Asymptote: x = 2
senkr. Asymptote: x = 2
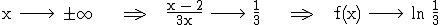
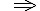 waagr. Asymptote: y =
waagr. Asymptote: y = 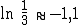 Nullstelle von f:
Nullstelle von f:
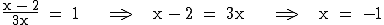 1.2
1.2 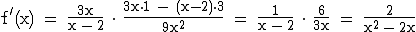 > 0 in D(f)
> 0 in D(f)
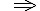 f steigt echt monoton in
f steigt echt monoton in 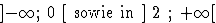 .
1.3
.
1.3  1.4 F '(x) = f(x) = 0
1.4 F '(x) = f(x) = 0 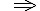 x = –1
f wechselt bei x = –1 von – nach +
x = –1
f wechselt bei x = –1 von – nach +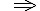 F hat bei x = –1 einen Tiefpunkt.
F ''(x) = f '(x) > 0 in D(F)
F hat bei x = –1 einen Tiefpunkt.
F ''(x) = f '(x) > 0 in D(F) 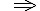 Der Graph von F ist in ganz D(F) linksgekrümmt.
2.1 2x – 4 = 0
Der Graph von F ist in ganz D(F) linksgekrümmt.
2.1 2x – 4 = 0 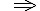 x = 2
x = 2 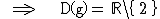 Der Nenner wechselt bei x = 2 von – nach + und der Zähler ist dort positiv. Also gilt:
Der Nenner wechselt bei x = 2 von – nach + und der Zähler ist dort positiv. Also gilt:
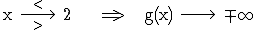 Folglich ist x = 2 eine senkrechte Asymptote.
Da der Zählergrad von g um 1 größer ist als der Nennergrad, gibt es außerdem eine schiefe
Asymptote, deren Gleichung durch Polynomdivision ermittelt wird:
Folglich ist x = 2 eine senkrechte Asymptote.
Da der Zählergrad von g um 1 größer ist als der Nennergrad, gibt es außerdem eine schiefe
Asymptote, deren Gleichung durch Polynomdivision ermittelt wird:
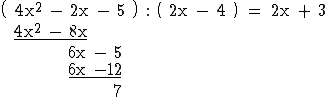 Also lautet die Gleichung der schiefen Asymptote y = 2x + 3.
2.2 Der Graph von g verläuft genau dann oberhalb seiner schiefen Asymptote y = 2x + 3, wenn
der echt-gebrochen-rationale Anteil von g positiv ist:
Also lautet die Gleichung der schiefen Asymptote y = 2x + 3.
2.2 Der Graph von g verläuft genau dann oberhalb seiner schiefen Asymptote y = 2x + 3, wenn
der echt-gebrochen-rationale Anteil von g positiv ist:
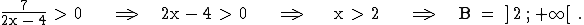 2.3
2.3 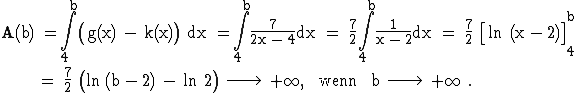 3.1 p(0) =
3.1 p(0) = 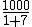 = 125 ;
= 125 ; 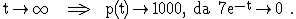
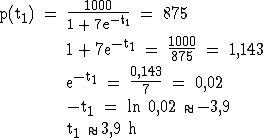 3.2
3.2 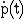 gibt das momentane Wachstum der Anzahl der Pilze zum Zeitpunkt t an.
gibt das momentane Wachstum der Anzahl der Pilze zum Zeitpunkt t an.
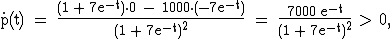 da Zähler und Nenner positiv sind.
Also nimmt die Anzahl der Pilze im gesamten Beobachtungszeitraum echt monoton zu.
3.3
3.4
da Zähler und Nenner positiv sind.
Also nimmt die Anzahl der Pilze im gesamten Beobachtungszeitraum echt monoton zu.
3.3
3.4