Durch die Aufgabe 3.2 wissen wir, dass die Geraden g
und h sowie der Punkt T auf der Ebene F liegen. Auch entnehmen wir daraus,
dass die Ebene F parallel zur 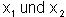 - Basisebene
liegt.
- Basisebene
liegt.
Gleichung der Geraden i durch die Punkte R und
S.
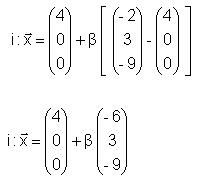
Ebenengleichung 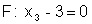
Schnittpunkt der Geraden i und der Ebene F
ausrechnen.
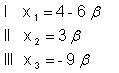 I und II wird nicht
gebraucht!(siehe Aufgabe 3.2)
I und II wird nicht
gebraucht!(siehe Aufgabe 3.2)
III. in die Ebene F einsetzen
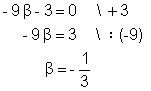
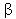 in i einsetzen
in i einsetzen
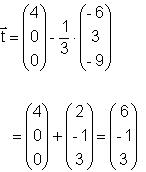
 Punkt
Punkt 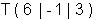
Nun stelle ich eine Hilfsgerade m auf, die durch T
geht und Parallel zur 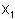 - Achse ist.
- Achse ist.
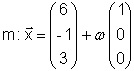
Die Hilfsgerade m liegt auch auf der Ebene
F!
Nun wird m mit g geschnitten. Diesen Schnittpunkt
nennen wir P.
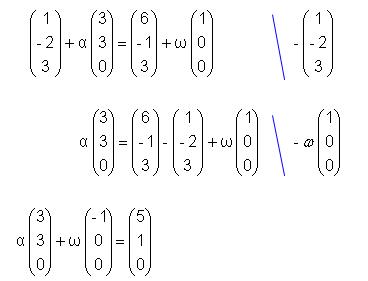
Die Umformung nach Gauß erübrigt sich, da bereits
genügend Nullen vorhanden sind. Wir erhalten
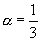 und
und  .
.
Einsetzen in die Gerade m:
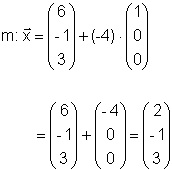
 Schnittpunkt
Schnittpunkt 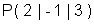
Die Geraden m und h werden geschnitten. Diesen
Schnittpunkt nennen wir Q.
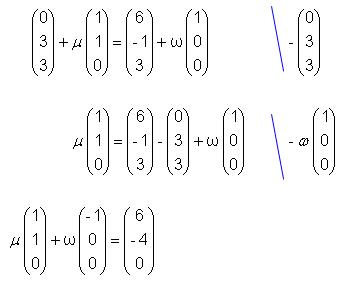
Wie oben erhalten wir sofort 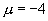 und
und 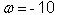
Einsetzen in die Gerade m
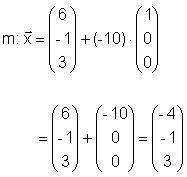
 Schnittpunkt
Schnittpunkt 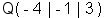
Logische Überlegung:
Nun ordnet man die drei Punkte nach ihren
x1-Werten auf der Hilfsgeraden m an.
Ebene F
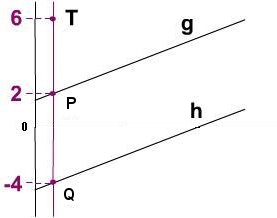 Somit ist die Skizze a zutreffend.
Somit ist die Skizze a zutreffend.
Bemerkung:
Statt der Hilfsgeraden m könnten wir auch die Gerade AT nehmen (A liegt
auf g), dann den Schnittpunkt mit h berechnen und ähnlich wie oben
überlegen, wie dieser Schnittpunkt bezüglich A und T liegt.
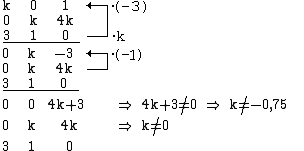 d. h. genau für
d. h. genau für 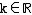 \{–0,75 ; 0} ist der Rang der Matrix gleich 3, sind also die drei Vektoren
linear unabhängig und bilden daher eine Basis des
\{–0,75 ; 0} ist der Rang der Matrix gleich 3, sind also die drei Vektoren
linear unabhängig und bilden daher eine Basis des 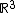 .
2.1 E: ax1 + bx2 + cx3 = d
A, B und C in E eingesetzt ergibt ein LGS:
.
2.1 E: ax1 + bx2 + cx3 = d
A, B und C in E eingesetzt ergibt ein LGS:
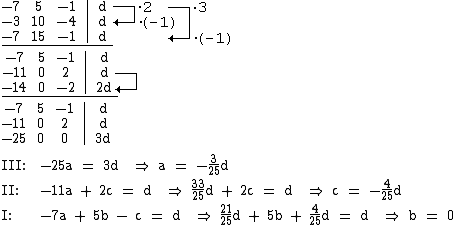 Für d = –25 ergeben sich a = 3, b = 0 und c = 4.
Also besitzt E die Gleichung 3x1 + 4x3 + 25 = 0 und ist somit parallel zur x2-Achse.
2.2
Für d = –25 ergeben sich a = 3, b = 0 und c = 4.
Also besitzt E die Gleichung 3x1 + 4x3 + 25 = 0 und ist somit parallel zur x2-Achse.
2.2 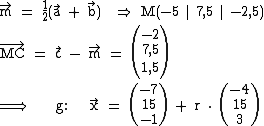 2.3
2.3 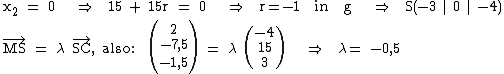 Also liegt S bzgl. M auf der „Gegenseite“ von C, genauer: M ist die Mitte zwischen S und C.
Skizze:
Also liegt S bzgl. M auf der „Gegenseite“ von C, genauer: M ist die Mitte zwischen S und C.
Skizze: 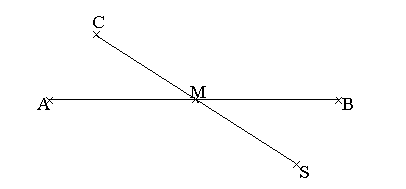 2.4 ha in E:
3(–1 + 8s) + 4(7 – 6s) + 25 = 0
–3 + 24s + 28 – 24s + 25 = 0
50 = 0 : falsche Aussage!
Also haben die Geraden ha mit E keinen gemeinsamen Punkt, sind also zu E echt parallel.
2.4 ha in E:
3(–1 + 8s) + 4(7 – 6s) + 25 = 0
–3 + 24s + 28 – 24s + 25 = 0
50 = 0 : falsche Aussage!
Also haben die Geraden ha mit E keinen gemeinsamen Punkt, sind also zu E echt parallel.
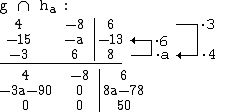 Man erkennt, dass für a = –30 der Rang der Koeffizientenmatrix gleich 1 und sonst 2 ist.
Der Rang der erweiterten Koeffizientenmatrix ist jeweils um 1 größer.
Daraus folgt, dass die Geraden g und ha für a = –30 echt parallel und sonst windschief sind.
Rechnerisch einfacher, aber gedanklich anspruchsvoller, ist der folgende Lösungsweg:
Eben wurde gezeigt, dass die Geraden ha echt parallel zu E verlaufen, und nach Aufgabe 2.2 ist klar,
dass g in E liegt. Damit ist klar, dass ha und g nur entweder echt parallel oder windschief
verlaufen können. Um herauszufinden, wann welcher Fall zutrifft, braucht man also nur die beiden
Richtungsvektoren zu vergleichen:
Man erkennt, dass für a = –30 der Rang der Koeffizientenmatrix gleich 1 und sonst 2 ist.
Der Rang der erweiterten Koeffizientenmatrix ist jeweils um 1 größer.
Daraus folgt, dass die Geraden g und ha für a = –30 echt parallel und sonst windschief sind.
Rechnerisch einfacher, aber gedanklich anspruchsvoller, ist der folgende Lösungsweg:
Eben wurde gezeigt, dass die Geraden ha echt parallel zu E verlaufen, und nach Aufgabe 2.2 ist klar,
dass g in E liegt. Damit ist klar, dass ha und g nur entweder echt parallel oder windschief
verlaufen können. Um herauszufinden, wann welcher Fall zutrifft, braucht man also nur die beiden
Richtungsvektoren zu vergleichen:
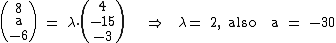 Daraus folgt wieder, dass die Geraden g und ha für a = –30 echt parallel und sonst windschief sind.
3.1 Verflechtungstabelle:
Daraus folgt wieder, dass die Geraden g und ha für a = –30 echt parallel und sonst windschief sind.
3.1 Verflechtungstabelle:
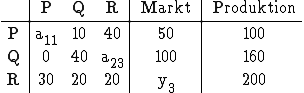 Aus der Tabelle folgt: a11 = 0; a23 = 20; y3 = 130
Die Inputmatrix A ergibt sich, indem die P-Spalte durch 100, die Q-Spalte durch 160
und die R-Spalte durch 200 dividiert wird:
Aus der Tabelle folgt: a11 = 0; a23 = 20; y3 = 130
Die Inputmatrix A ergibt sich, indem die P-Spalte durch 100, die Q-Spalte durch 160
und die R-Spalte durch 200 dividiert wird:
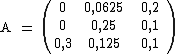 3.2
3.2 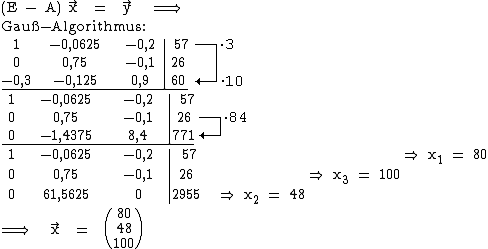 3.3
3.3 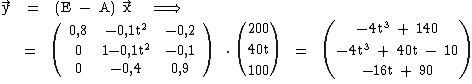 Die Summe der Marktabgaben beträgt also S(t) = –8t3 + 24t + 220 .
Bestimmung des Maximums: S '(t) = –24t2 + 24 = 0
Die Summe der Marktabgaben beträgt also S(t) = –8t3 + 24t + 220 .
Bestimmung des Maximums: S '(t) = –24t2 + 24 = 0 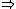 t = 1
(t = –1 ist uninteressant, denn es liegt nicht zwischen 0,5 und 3.)
Bei t = 1 liegt ein Maximum von S vor, da dort die Steigung von + nach – wechselt.
Da S nur für t < –1 größer werden kann als bei t = 1, wird die Summe der Marktabgaben
im Intervall [0,5 ; 3] für t = 1 am größten.
t = 1
(t = –1 ist uninteressant, denn es liegt nicht zwischen 0,5 und 3.)
Bei t = 1 liegt ein Maximum von S vor, da dort die Steigung von + nach – wechselt.
Da S nur für t < –1 größer werden kann als bei t = 1, wird die Summe der Marktabgaben
im Intervall [0,5 ; 3] für t = 1 am größten.
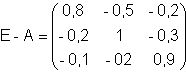
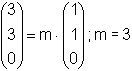 , g und h haben die gleiche Richtung
, g und h haben die gleiche Richtung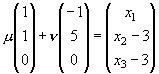
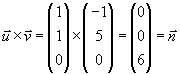
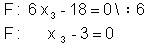
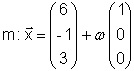
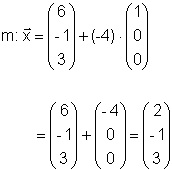
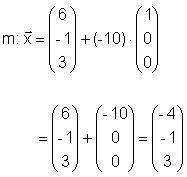
 Somit ist die Skizze a zutreffend.
Somit ist die Skizze a zutreffend.