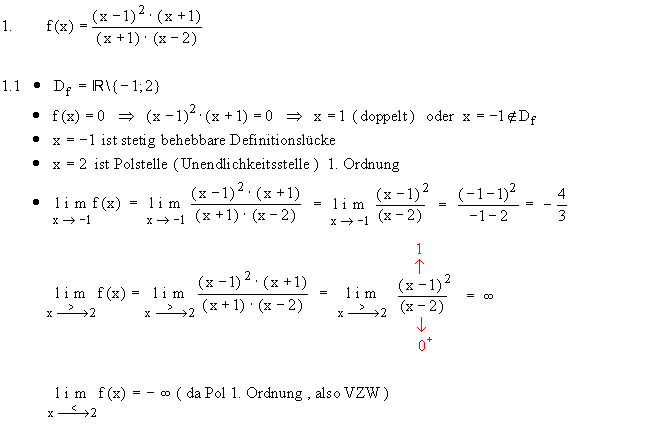
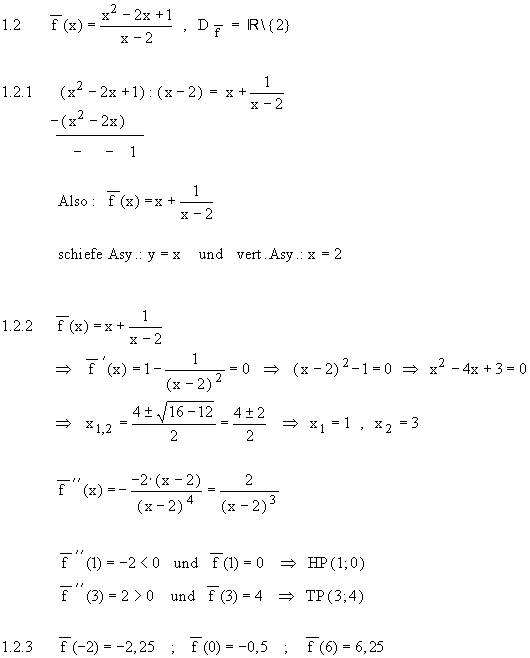
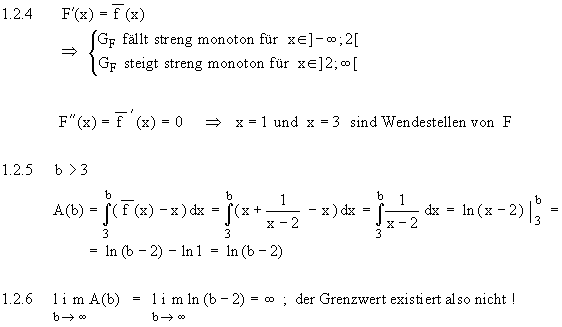
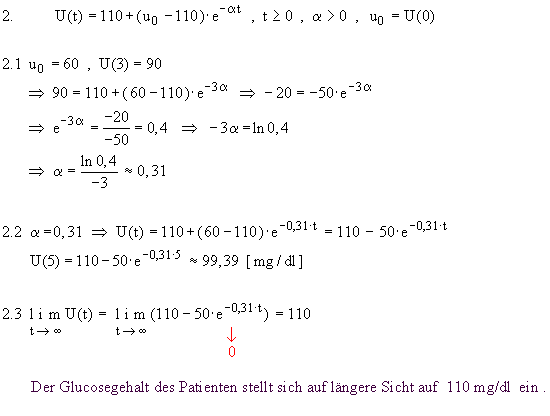
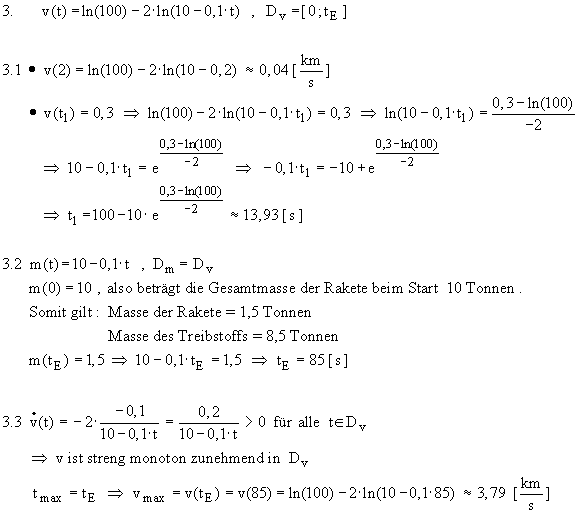
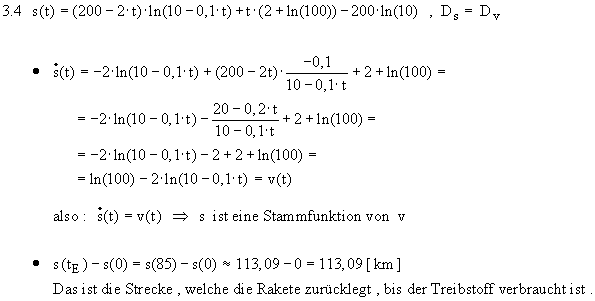
Abschlussprüfung zur Erlangung der fachgebundenen Hochschulreife
Frühjahr 2007

A I:   Lösungen

A II:   Lösungen

1.1	


1.2	

	 


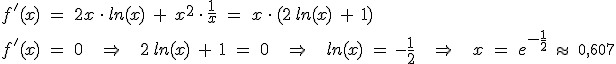
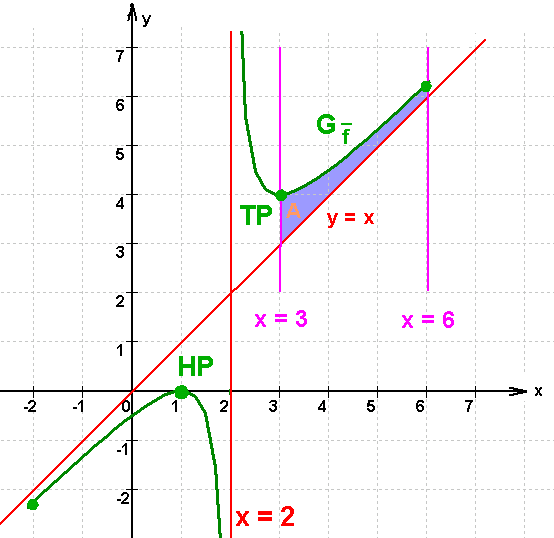
1.3	, da der nicht-logarithmische Faktor gegen 0 strebt
	 und sich gegen den logarithmischen Faktor durchsetzt.

	     (Begründung wie oben)


1.4	Wegen  muss f '
	 in diesem Intervall einen kleinsten Wert, also der Graph von f einen
	 Wendepunkt haben.


1.5	




2.1	
	 x = 2  ist eine Polstelle zweiter Ordnung von g, also ohne Vorzeichenwechsel.
	


2.2	Schiefe Asymptote:  
	 Senkrechte Asymptote:  x = 2
	 Da der „Abweichungsterm“ von der schiefen Asymptote   immer kleiner 0 ist,
	 nähert sich der Graph von g der schiefen Asymptote von unten, wenn .


2.3	


2.4	
	 Der Wert des Integrals ist die Maßzahl der Fläche, die von dem Graphen von g
	 und den Achsen eingeschlossen wird.




3.1	


3.2	

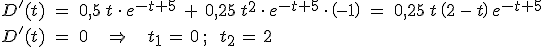
	  ist der gesuchte Wert, da hier das Vorzeichen von D'(t) von + nach – wechselt.


3.3	Nach 3.2 hat D bei  sein Maximum. Dieses beträgt .
	 Also findet eine Ausuferung nicht statt.


3.4	, da der exponentielle Faktor gegen 0 geht 
	 und sich gegen den nicht-exponentiellen Faktor durchsetzt.


3.5	
	 Also ist V eine Stammfunktion von D.
	 
	 Das Ergebnis besagt, dass in den ersten 6 Stunden insgesamt 189,61 Kubikmeter Wasser
	 durch den Bach fließen.