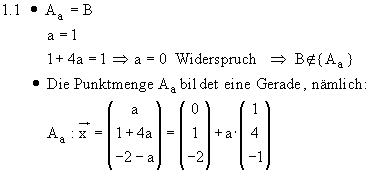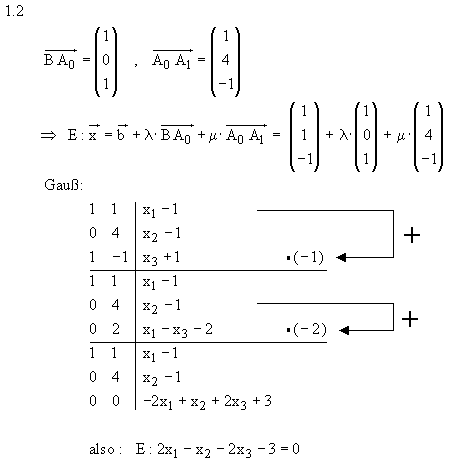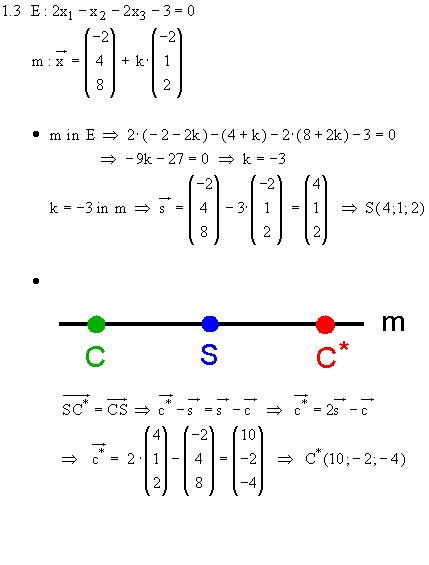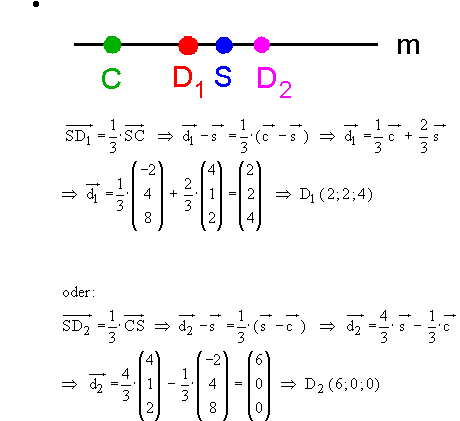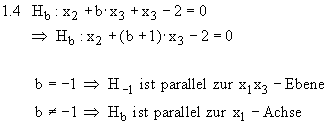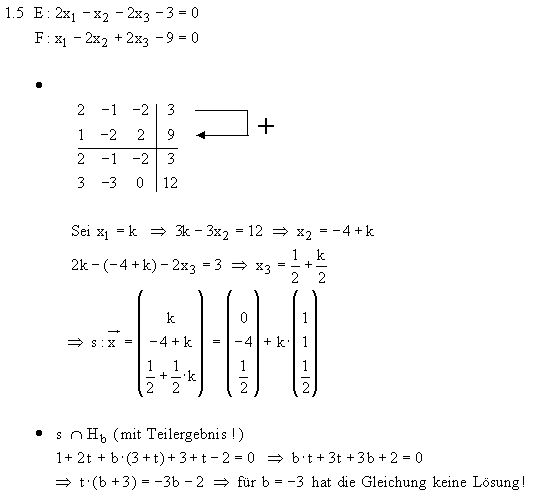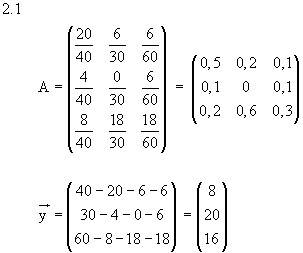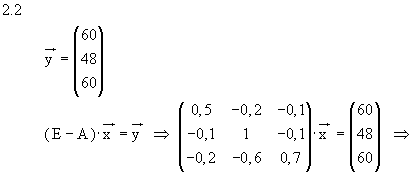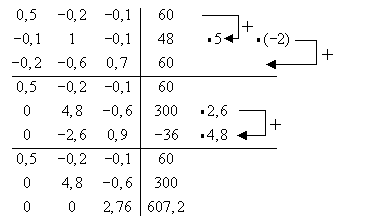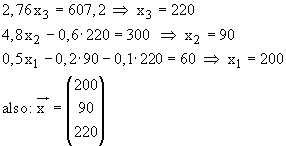Abschlussprüfung zur Erlangung der fachgebundenen
Hochschulreife
Frühjahr 2007
B I: Lösungen
1.1  ,
,  und
und 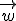 bilden genau dann eine Basis des
bilden genau dann eine Basis des 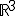 , wenn sich aus ihnen der Null-
vektor nur auf triviale Weise linear kombinieren lässt, d. h. wenn die Gleichung
, wenn sich aus ihnen der Null-
vektor nur auf triviale Weise linear kombinieren lässt, d. h. wenn die Gleichung
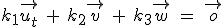 nur die Lösung
nur die Lösung 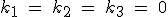 hat.
hat.
 Die zweite Gleichung
Die zweite Gleichung 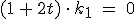 hat für
hat für 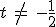 nur die Lösung
nur die Lösung 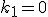 .
In diesem Fall ergeben die dritte und die erste Gleichung dann auch
.
In diesem Fall ergeben die dritte und die erste Gleichung dann auch 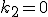 und
und 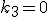 ,
so dass die drei Vektoren
,
so dass die drei Vektoren 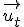 ,
, 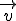 und
und 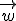 für alle
für alle 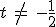 eine Basis des
eine Basis des 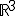 bilden.
Linearkombination von
bilden.
Linearkombination von 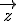 aus den drei Basisvektoren für t = 0:
aus den drei Basisvektoren für t = 0:
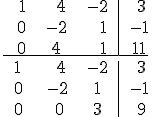 Die letzte Gleichung liefert
Die letzte Gleichung liefert 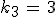 , womit sich aus der zweiten Gleichung
, womit sich aus der zweiten Gleichung 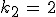 und dann aus der ersten Gleichung
und dann aus der ersten Gleichung 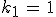 ergeben.
Also gilt:
ergeben.
Also gilt: 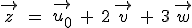 .
1.2 Das Gleichungssystem der drei Ebenen E, F und G führt genau zum zweiten Gauß-
Algorithmus von Aufgabe 1.1, so dass sich mit dessen schon bekannten Lösungen
der gemeinsame Ebenenpunkt S(1 | 2 | 3) ergibt. Daraus wie auch aus den Koeffizienten
der Ebenen F und G wird deutlich, dass diese nicht zueinander parallel verlaufen.
Da ihr Koeffizient von
.
1.2 Das Gleichungssystem der drei Ebenen E, F und G führt genau zum zweiten Gauß-
Algorithmus von Aufgabe 1.1, so dass sich mit dessen schon bekannten Lösungen
der gemeinsame Ebenenpunkt S(1 | 2 | 3) ergibt. Daraus wie auch aus den Koeffizienten
der Ebenen F und G wird deutlich, dass diese nicht zueinander parallel verlaufen.
Da ihr Koeffizient von 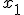 jeweils 0 ist, verlaufen beide parallel zur
jeweils 0 ist, verlaufen beide parallel zur 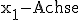 .
Die Differenz ihrer Gleichungen liefert
.
Die Differenz ihrer Gleichungen liefert 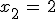 . Setzt man diesen Wert in F ein,
so ergibt sich
. Setzt man diesen Wert in F ein,
so ergibt sich 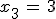 , so dass z. B. der Punkt P(0 | 2 | 3) auf F und G liegt.
Wegen der Parallelität von F und G zur
, so dass z. B. der Punkt P(0 | 2 | 3) auf F und G liegt.
Wegen der Parallelität von F und G zur 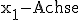 müssen folglich auch Q(1 | 2 | 3)
und R(2 | 2 | 3) auf F und G liegen.
1.3 Da G, nicht aber E wegen seines von 0 verschiedenen Koeffizienten von
müssen folglich auch Q(1 | 2 | 3)
und R(2 | 2 | 3) auf F und G liegen.
1.3 Da G, nicht aber E wegen seines von 0 verschiedenen Koeffizienten von 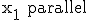 zur
zur 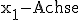 verläuft, ist nur Zeichnung b) richtig.
2 Die gesuchte Ebene H muss die
verläuft, ist nur Zeichnung b) richtig.
2 Die gesuchte Ebene H muss die 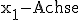 enthalten. Man wählt z. B. die Ebene,
die zudem durch den Punkt P(0 | 1 | 1) verläuft.
Deren Parameterform lautet:
enthalten. Man wählt z. B. die Ebene,
die zudem durch den Punkt P(0 | 1 | 1) verläuft.
Deren Parameterform lautet: 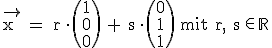 Ihre Koordinatenform enthält
Ihre Koordinatenform enthält 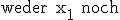 eine Konstante. Da P(0 | 1 | 1) auf H liegt,
lautet die Koordinatenform von H:
eine Konstante. Da P(0 | 1 | 1) auf H liegt,
lautet die Koordinatenform von H: 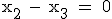 .
3.1 Input-Output-Tabelle:
.
3.1 Input-Output-Tabelle:
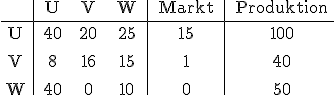 3.2
3.2 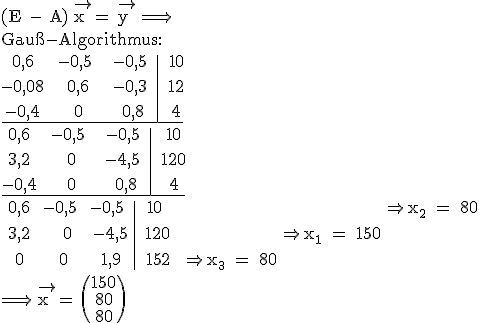 3.3.1
3.3.1 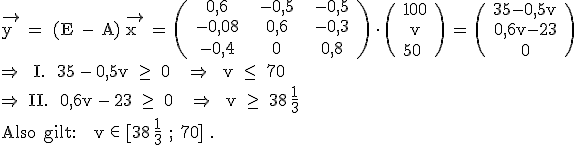 3.3.2 Mit
3.3.2 Mit 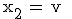 folgt aus 3.3.1:
folgt aus 3.3.1:
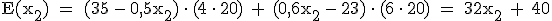 3.3.3
3.3.3 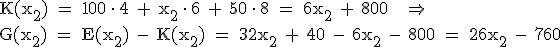 Da der Graph von G linear ansteigt, wird das Gewinnmaximum bei der größtmöglichen
Produktion von Werk V, also für
Da der Graph von G linear ansteigt, wird das Gewinnmaximum bei der größtmöglichen
Produktion von Werk V, also für 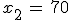 erzielt.
Das Gewinnmaximum beträgt demnach G(70) = (26 · 70 – 760) GE = 1060 GE.
erzielt.
Das Gewinnmaximum beträgt demnach G(70) = (26 · 70 – 760) GE = 1060 GE.
B II: Lösungen
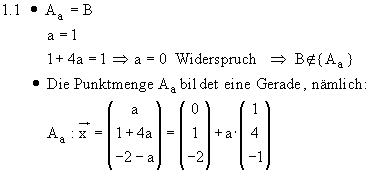
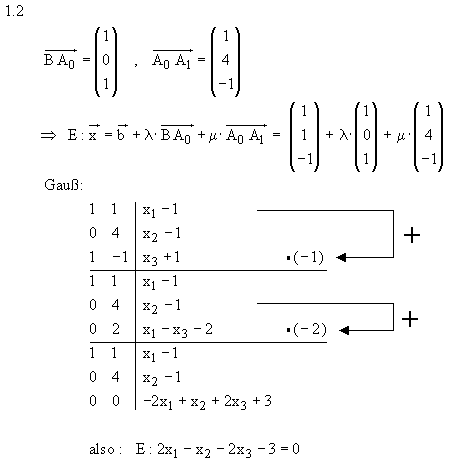
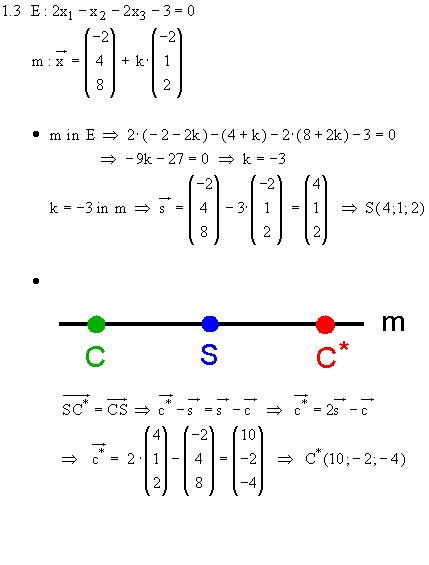
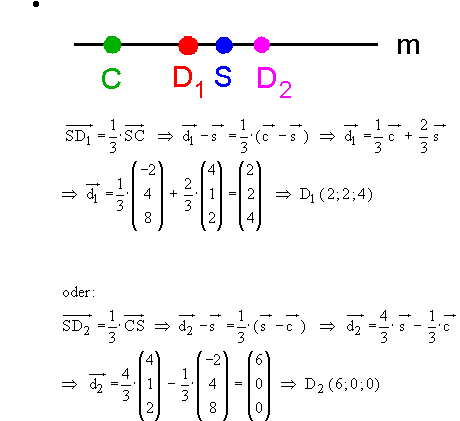
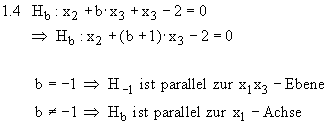
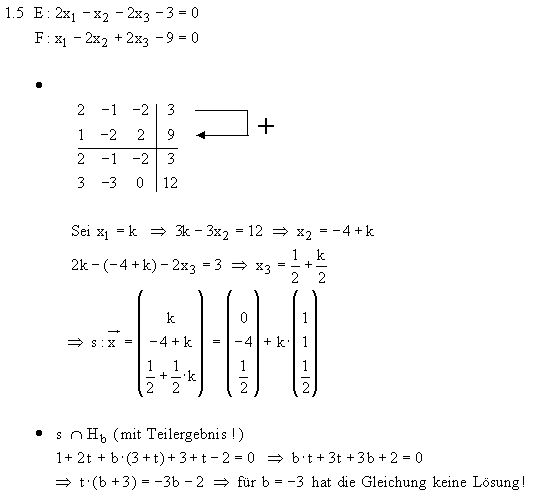
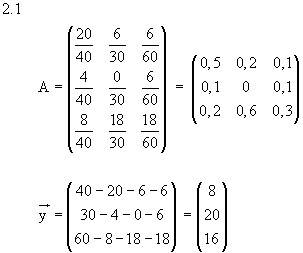
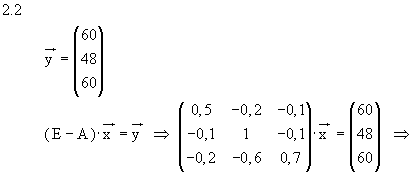
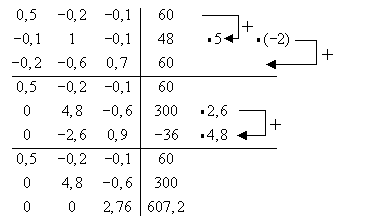
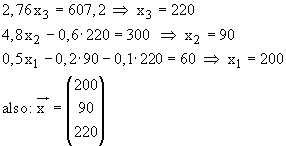

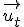 ,
, 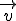 und
und 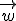 bilden genau dann eine Basis des
bilden genau dann eine Basis des 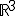 , wenn sich aus ihnen der Null-
vektor nur auf triviale Weise linear kombinieren lässt, d. h. wenn die Gleichung
, wenn sich aus ihnen der Null-
vektor nur auf triviale Weise linear kombinieren lässt, d. h. wenn die Gleichung
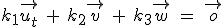 nur die Lösung
nur die Lösung 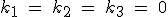 hat.
hat.
 Die zweite Gleichung
Die zweite Gleichung 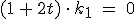 hat für
hat für 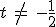 nur die Lösung
nur die Lösung 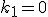 .
In diesem Fall ergeben die dritte und die erste Gleichung dann auch
.
In diesem Fall ergeben die dritte und die erste Gleichung dann auch 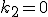 und
und 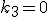 ,
so dass die drei Vektoren
,
so dass die drei Vektoren 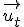 ,
, 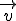 und
und 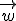 für alle
für alle 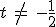 eine Basis des
eine Basis des 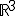 bilden.
Linearkombination von
bilden.
Linearkombination von 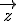 aus den drei Basisvektoren für t = 0:
aus den drei Basisvektoren für t = 0:
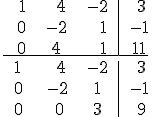 Die letzte Gleichung liefert
Die letzte Gleichung liefert 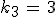 , womit sich aus der zweiten Gleichung
, womit sich aus der zweiten Gleichung 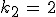 und dann aus der ersten Gleichung
und dann aus der ersten Gleichung 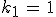 ergeben.
Also gilt:
ergeben.
Also gilt: 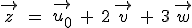 .
1.2 Das Gleichungssystem der drei Ebenen E, F und G führt genau zum zweiten Gauß-
Algorithmus von Aufgabe 1.1, so dass sich mit dessen schon bekannten Lösungen
der gemeinsame Ebenenpunkt S(1 | 2 | 3) ergibt. Daraus wie auch aus den Koeffizienten
der Ebenen F und G wird deutlich, dass diese nicht zueinander parallel verlaufen.
Da ihr Koeffizient von
.
1.2 Das Gleichungssystem der drei Ebenen E, F und G führt genau zum zweiten Gauß-
Algorithmus von Aufgabe 1.1, so dass sich mit dessen schon bekannten Lösungen
der gemeinsame Ebenenpunkt S(1 | 2 | 3) ergibt. Daraus wie auch aus den Koeffizienten
der Ebenen F und G wird deutlich, dass diese nicht zueinander parallel verlaufen.
Da ihr Koeffizient von 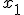 jeweils 0 ist, verlaufen beide parallel zur
jeweils 0 ist, verlaufen beide parallel zur 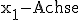 .
Die Differenz ihrer Gleichungen liefert
.
Die Differenz ihrer Gleichungen liefert 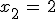 . Setzt man diesen Wert in F ein,
so ergibt sich
. Setzt man diesen Wert in F ein,
so ergibt sich 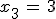 , so dass z. B. der Punkt P(0 | 2 | 3) auf F und G liegt.
Wegen der Parallelität von F und G zur
, so dass z. B. der Punkt P(0 | 2 | 3) auf F und G liegt.
Wegen der Parallelität von F und G zur 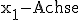 müssen folglich auch Q(1 | 2 | 3)
und R(2 | 2 | 3) auf F und G liegen.
1.3 Da G, nicht aber E wegen seines von 0 verschiedenen Koeffizienten von
müssen folglich auch Q(1 | 2 | 3)
und R(2 | 2 | 3) auf F und G liegen.
1.3 Da G, nicht aber E wegen seines von 0 verschiedenen Koeffizienten von 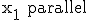 zur
zur 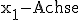 verläuft, ist nur Zeichnung b) richtig.
2 Die gesuchte Ebene H muss die
verläuft, ist nur Zeichnung b) richtig.
2 Die gesuchte Ebene H muss die 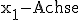 enthalten. Man wählt z. B. die Ebene,
die zudem durch den Punkt P(0 | 1 | 1) verläuft.
Deren Parameterform lautet:
enthalten. Man wählt z. B. die Ebene,
die zudem durch den Punkt P(0 | 1 | 1) verläuft.
Deren Parameterform lautet: 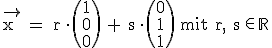 Ihre Koordinatenform enthält
Ihre Koordinatenform enthält 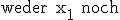 eine Konstante. Da P(0 | 1 | 1) auf H liegt,
lautet die Koordinatenform von H:
eine Konstante. Da P(0 | 1 | 1) auf H liegt,
lautet die Koordinatenform von H: 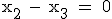 .
3.1 Input-Output-Tabelle:
.
3.1 Input-Output-Tabelle:
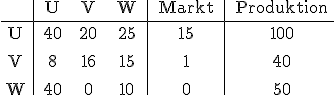 3.2
3.2 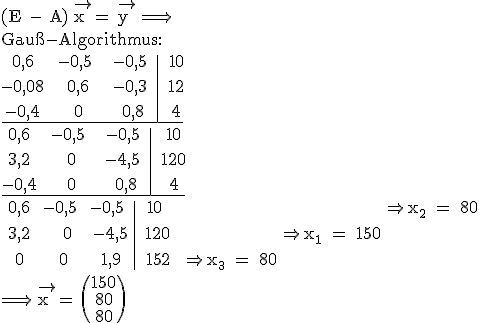 3.3.1
3.3.1 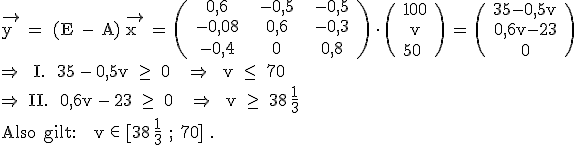 3.3.2 Mit
3.3.2 Mit 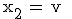 folgt aus 3.3.1:
folgt aus 3.3.1:
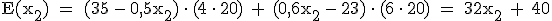 3.3.3
3.3.3 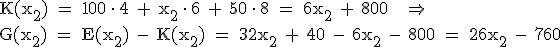 Da der Graph von G linear ansteigt, wird das Gewinnmaximum bei der größtmöglichen
Produktion von Werk V, also für
Da der Graph von G linear ansteigt, wird das Gewinnmaximum bei der größtmöglichen
Produktion von Werk V, also für 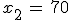 erzielt.
Das Gewinnmaximum beträgt demnach G(70) = (26 · 70 – 760) GE = 1060 GE.
erzielt.
Das Gewinnmaximum beträgt demnach G(70) = (26 · 70 – 760) GE = 1060 GE.