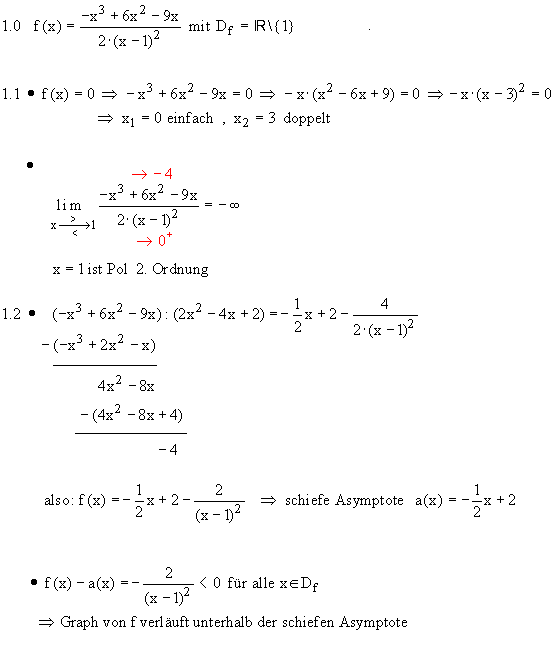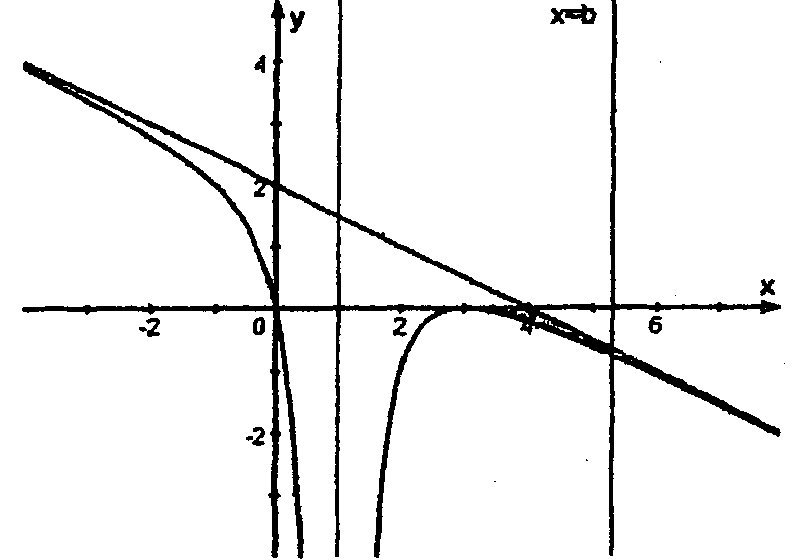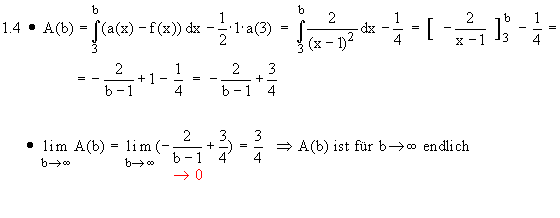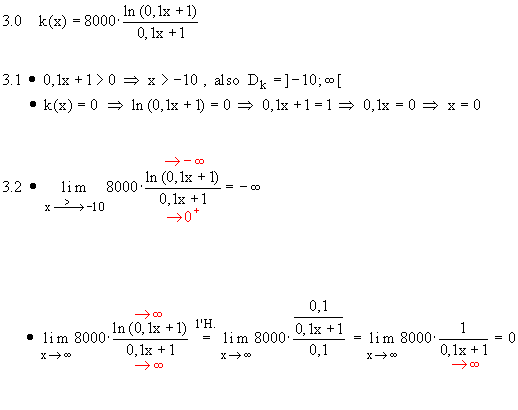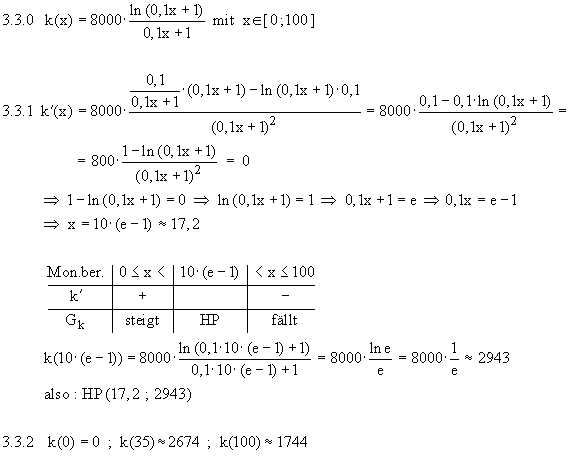 1.2
1.2 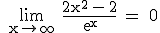 , da Zähler und Nenner gegen +∞ gehen und die e-Funktion überwiegt.
Also ist y = 0 eine waagrechte Asymptote.
, da Zähler und Nenner gegen +∞ gehen und die e-Funktion überwiegt.
Also ist y = 0 eine waagrechte Asymptote.
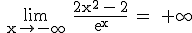 , da der Zähler gegen +∞ und der Nenner gegen +0 geht.
1.3
, da der Zähler gegen +∞ und der Nenner gegen +0 geht.
1.3  1.4
1.4 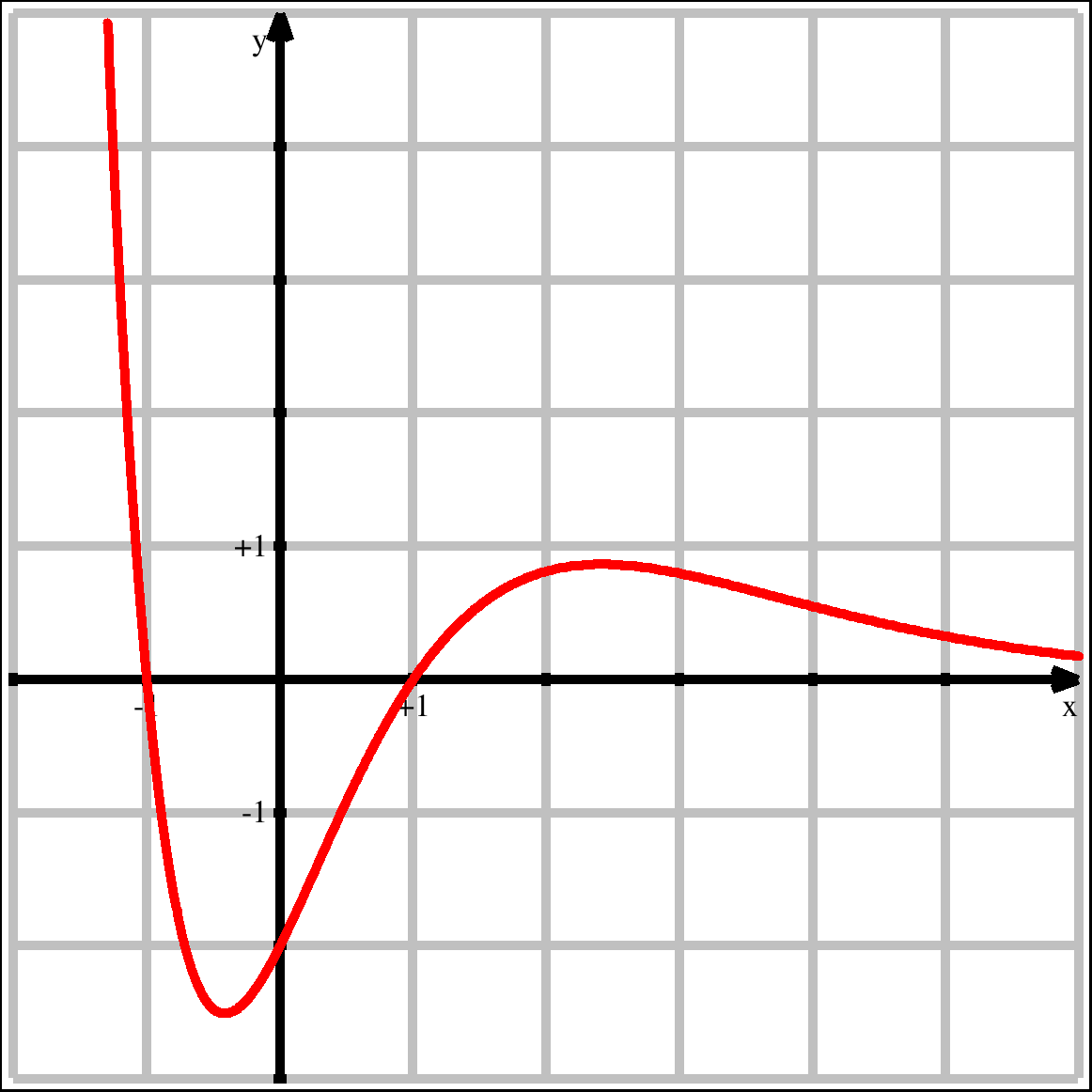 f(-1,2) = 2,92f(4) = 0,55f(6) = 0,17
1.5
f(-1,2) = 2,92f(4) = 0,55f(6) = 0,17
1.5 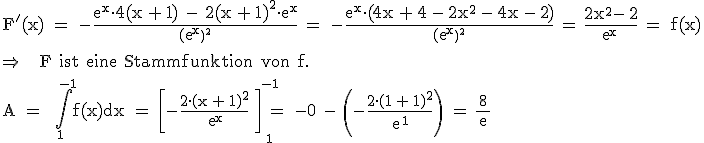 1.6.1
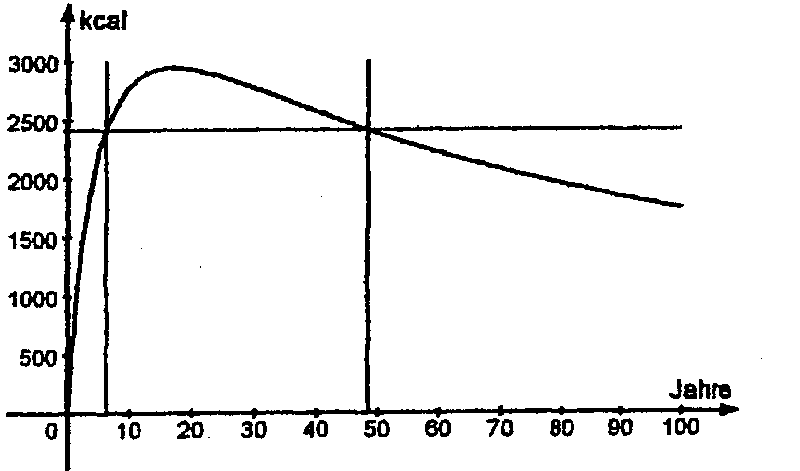
1.6.1 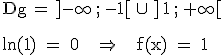 Die Gerade y = 1 schneidet den Graphen von f nur einmal, nämlich etwas links von x = –1.
Also hat g genau eine Nullstelle.
1.6.2
Die Gerade y = 1 schneidet den Graphen von f nur einmal, nämlich etwas links von x = –1.
Also hat g genau eine Nullstelle.
1.6.2 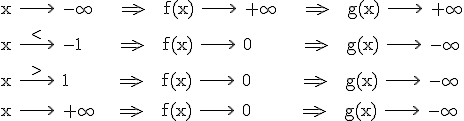 1.6.3
1.6.3 Da die Logarithmusfunktion echt monoton steigt, hat sie in ihrem Definitionsbereich
dasselbe Monotonieverhalten, also auch dieselben Minimal- und Maximalstellen wie
ihre Argumentfunktion. Da die Minimalstelle x=–0,41 von f nicht, wohl aber deren
Maximalstelle x=2,41 in 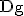 liegt, hat g hier ebenfalls ihr (einziges) relatives Maximum,
nämlich g(2,41) = ln (0,86) = –0,15.
Also: HOP (2,41 | –0,15)
liegt, hat g hier ebenfalls ihr (einziges) relatives Maximum,
nämlich g(2,41) = ln (0,86) = –0,15.
Also: HOP (2,41 | –0,15)
2.1 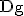 liegt, hat g hier ebenfalls ihr (einziges) relatives Maximum,
nämlich g(2,41) = ln (0,86) = –0,15.
Also: HOP (2,41 | –0,15)
liegt, hat g hier ebenfalls ihr (einziges) relatives Maximum,
nämlich g(2,41) = ln (0,86) = –0,15.
Also: HOP (2,41 | –0,15)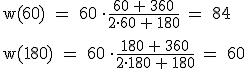 2.2
2.2 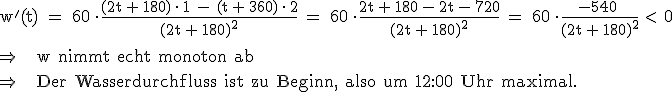 2.3.1
2.3.1 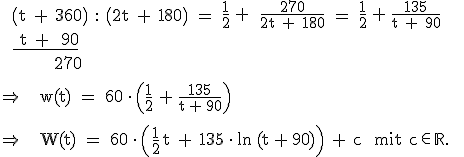 2.3.2
2.3.2 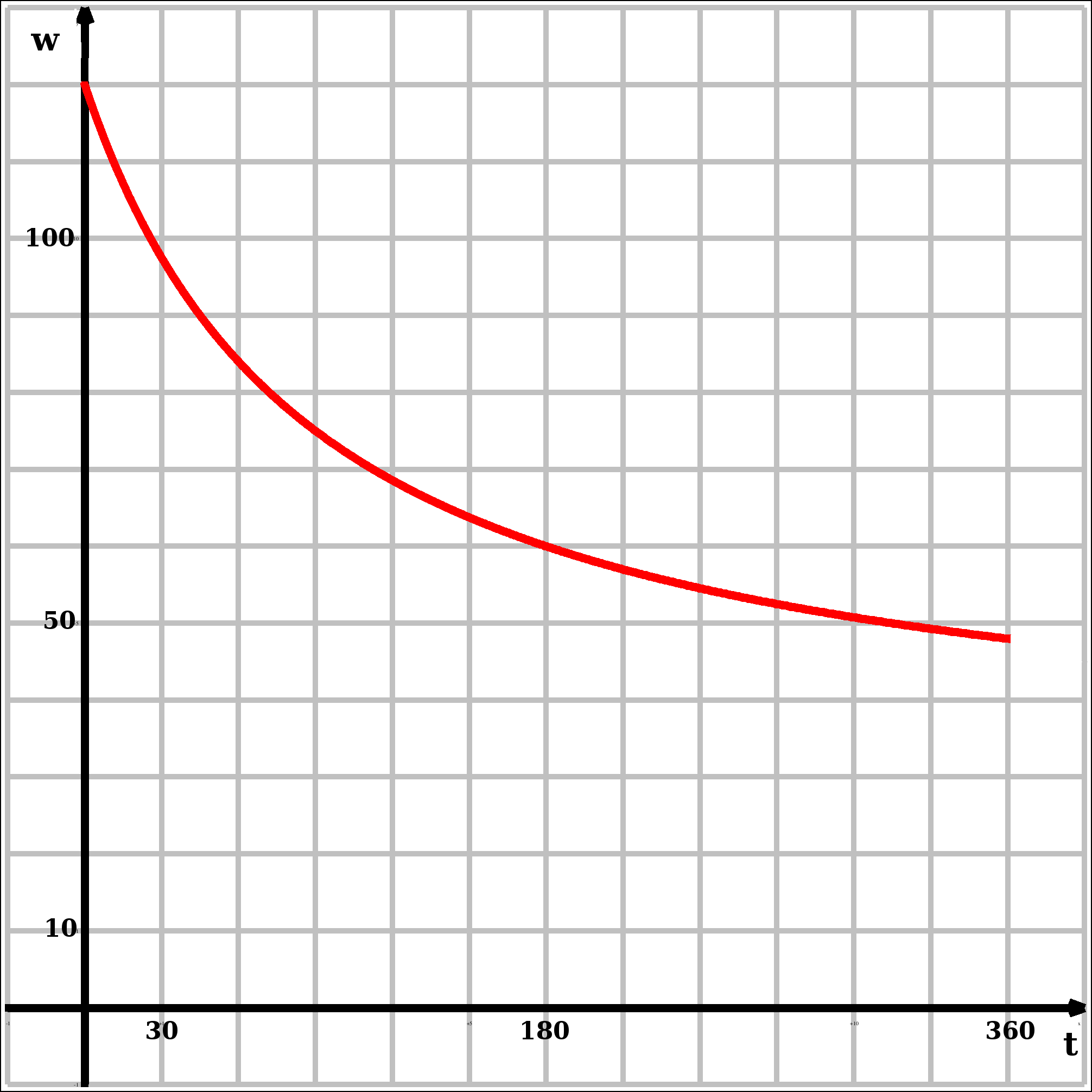 2.3.3
2.3.3