Nr.
Lösungsvorschlag A I
BE
1.1
D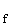 =IR \{0;1}; f(x)=
=IR \{0;1}; f(x)=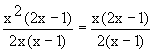 ; Nullstelle: x=0,5; x
; Nullstelle: x=0,5; x  0: f(x)
0: f(x)  0, d.h. x=0 ist stetig behebbare Def.lücke. x
0, d.h. x=0 ist stetig behebbare Def.lücke. x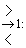 Z(x)
Z(x)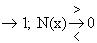 : f(x)
: f(x)  ±∞ , d.h. x=1 ist Unendlichkeitsstelle.
±∞ , d.h. x=1 ist Unendlichkeitsstelle.
7
1.2
(2x -x): (2x-2)=x+0,5+
-x): (2x-2)=x+0,5+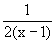 ; senkrechte Asymptote: x=1; schiefe Asymptote:
; senkrechte Asymptote: x=1; schiefe Asymptote: 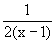 >0 für x>1, d.h. G(f) verläuft für 1<x<∞ oberhalb und für –∞<x<0 bzw. 0<x<1 unterhalb der Asymptote.
>0 für x>1, d.h. G(f) verläuft für 1<x<∞ oberhalb und für –∞<x<0 bzw. 0<x<1 unterhalb der Asymptote.
7
1.3
f ´(x)=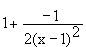 =
=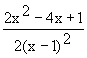
 f ´(x)=0 für x= 1±
f ´(x)=0 für x= 1±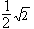 ; VZW von Z an der Stelle x= 1+
; VZW von Z an der Stelle x= 1+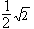 von - nach + : Minimalstelle, bei x =1–
von - nach + : Minimalstelle, bei x =1–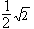 ist der VZW umgekehrt: Maximalstelle. HP(0,29|0,09) ; TP(1,71|2,91)
ist der VZW umgekehrt: Maximalstelle. HP(0,29|0,09) ; TP(1,71|2,91)
8
1.4
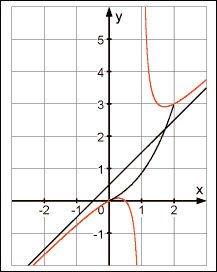
f(–3)≈–2,62
f(3)≈3,75
5
1.5
F ´(x)= c(2x+1+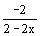 )= 2c(x+0,5+
)= 2c(x+0,5+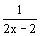 )= 2c·f(x); F´(x)=f(x)
)= 2c·f(x); F´(x)=f(x) 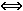 c=0,5.
c=0,5. 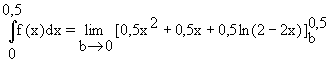 =
= 
8
2.1
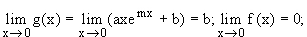 d.h. g ist stetig bei x=0 für b=0.
d.h. g ist stetig bei x=0 für b=0.
Für 0<x<2 ist g´(x)=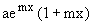 ;
; 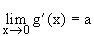 und
und 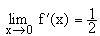 , also ist g bei x=0 differenzierbar, falls b=0 und a=0,5 ist. g ist stetig bei x=2, falls
, also ist g bei x=0 differenzierbar, falls b=0 und a=0,5 ist. g ist stetig bei x=2, falls 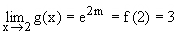 ist, also für m=0,5ln3.
ist, also für m=0,5ln3.
8
2.2
g´(x)=0,5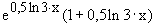 ;
;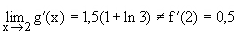 , d.h. g ist bei x=2 nicht diff.bar.
, d.h. g ist bei x=2 nicht diff.bar.
g´´(x)=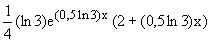 ; alle Faktoren sind für x>0 positiv, also
; alle Faktoren sind für x>0 positiv, also
ist g´´(x) positiv in ]0;2[, d.h. Gg ist linksgekrümmt. + Zeichnung
7
3.1
d(50)=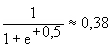 ; d(100)=
; d(100)=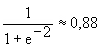 . Der Durchmesser beträgt 0,38 m bzw. 0,88 m
. Der Durchmesser beträgt 0,38 m bzw. 0,88 m
2
3.2
t 0: d(t)
0: d(t) 
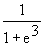 ≈0,047; t
≈0,047; t ∞: d(t)
∞: d(t)  1. Dieses mathematische Modell geht davon aus, dass der Fichtendurchmesser nie größer als 1,0 Meter wird und dass ein Setzling bereits einen Durchmesser von ca. 5 cm besitzt.
1. Dieses mathematische Modell geht davon aus, dass der Fichtendurchmesser nie größer als 1,0 Meter wird und dass ein Setzling bereits einen Durchmesser von ca. 5 cm besitzt.
4
3.3
Aus U=1,80 m ergibt sich mit U=dπ für die Maßzahl: d≈0,573.
1+e–0,05(t–60)= 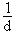 ; –0,05(t–60) = ln(
; –0,05(t–60) = ln(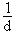 –1); t = 60–20ln(
–1); t = 60–20ln(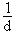 –1); t ≈ 66
–1); t ≈ 66
Ein solcher Baum ist ca. 66 Jahre alt.
4
Σ =
60
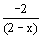 ; für x<2 ist g´(x)<0, also ist G(g) streng monoton fallend;
; für x<2 ist g´(x)<0, also ist G(g) streng monoton fallend; 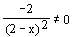 ;
;

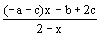 ; S´(x)≡g(x) für a=2
; S´(x)≡g(x) für a=2

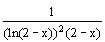 ; zwar ist f´(x)>0 in D(f); das Monotoniekriterium ist aber nur auf den (größtmögl.)Intervallen I1=]–∞;1[ sowie I2=]1;2[ anwendbar.
; zwar ist f´(x)>0 in D(f); das Monotoniekriterium ist aber nur auf den (größtmögl.)Intervallen I1=]–∞;1[ sowie I2=]1;2[ anwendbar.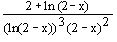 ; f ''(x)=0 für xw=2–e–2; da der Zähler von f '' streng mon. abnimmt (vgl.1.2), wechselt f ''(x) das Vorzeichen, also hat G(f) einen Wendepkt.
; f ''(x)=0 für xw=2–e–2; da der Zähler von f '' streng mon. abnimmt (vgl.1.2), wechselt f ''(x) das Vorzeichen, also hat G(f) einen Wendepkt.

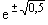
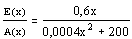 ; durch W(x)>1 wird gemessen, bei welchen Prod.zahlen der Ertrag größer als der Aufwand ist . W(x)>1
; durch W(x)>1 wird gemessen, bei welchen Prod.zahlen der Ertrag größer als der Aufwand ist . W(x)>1  ]500;1000[.
]500;1000[.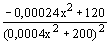 ; W´(x)=0
; W´(x)=0 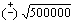 ≈707; W´ hat bei x≈707 VZW von + nach –, also (absolutes) Maximum; W(
≈707; W´ hat bei x≈707 VZW von + nach –, also (absolutes) Maximum; W(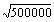 )≈1,06.
)≈1,06.