| 1 | Gegeben ist die reelle Funktion f : x 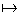 (2 – ln(x))·(2 + ln(x)) mit maximaler Definitionsmenge ID (2 – ln(x))·(2 + ln(x)) mit maximaler Definitionsmenge ID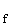 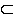 IR. IR. |
| 1.1 | Bestimmen Sie IDf und die Nullstellen von f und untersuchen Sie das Verhalten von f(x) an den Rändern der Definitionsmenge. (5 BE) |
| |
| 1.2 | Ermitteln Sie die Art und die Lage des Extrempunktes sowie die Koordinaten des Wendepunktes des Graphen von f (Nachweis ohne Verwendung der dritten Ableitung). (9 BE)
(Zwischenergebnis: f ' (x) = 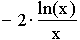 ) )
|
| |
| 1.3 | Stellen Sie die Gleichung der Wendetangente t des Graphen von f auf. Zeichnen Sie die Tangente t und den Graphen von f unter Verwendung der bisherigen Ergebnisse für x 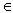 ] 0 ; 10 ] in ein kartesisches Koordinatensystem. (6 BE) ] 0 ; 10 ] in ein kartesisches Koordinatensystem. (6 BE) |
| |
| 1.4 | Bestimmen Sie die reellen Koeffizienten b und c so, dass die Funktion
F: x 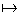 –x·(ln(x))2
+ bx·ln(x) + cx in IDf eine Stammfunktion von f ist, und berechnen Sie den Inhalt der endlichen Fläche, die der Graph von f mit der x-Achse einschließt. (10 BE) –x·(ln(x))2
+ bx·ln(x) + cx in IDf eine Stammfunktion von f ist, und berechnen Sie den Inhalt der endlichen Fläche, die der Graph von f mit der x-Achse einschließt. (10 BE) |
| |
| |
2 | Nun ist die Funktion g: x 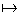 g(x) = g(x) = 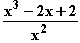 mit Definitionsmenge ID mit Definitionsmenge ID = ] 0 ; ∞ [ gegeben. = ] 0 ; ∞ [ gegeben. |
| |
| 2.1 | Begründen Sie durch eine genaue Untersuchung der Zählerfunktion, dass g keine Nullstelle besitzt. (5 BE) |
| |
| 2.2 | Zeigen Sie, dass der Graph von g für x > 1 stets unterhalb seiner schiefen Asymptote verläuft. Berechnen Sie sodann den Inhalt der endlichen Fläche, die der Graph von g für x 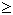 1 mit der Asymptoten und der Gerade x = 3 einschließt. (7 BE) 1 mit der Asymptoten und der Gerade x = 3 einschließt. (7 BE) |
| |
| |
| 3 | Ein Kubikzentimeter Kuhmilch enthielt 2 Stunden nach dem Melken 2824 Keime, eine weitere Stunde später 3389 Keime. Mit a( t ) werde die Anzahl der Keime zum Zeitpunkt t (in Stunden) bezeichnet, mit a0 die Anzahl der Keime zum Zeitpunkt t = 0 und mit k die Wachstumskonstante. Innerhalb eines gewissen Zeitintervalls [0 ; t0] gelte: a( t ) = a0·ekt. Auf Benennungen wird bei der Rechnung verzichtet. |
| |
| 3.1 | Bestimmen Sie a0 und k. (5 BE)
(Zur Kontrolle: a0 = 1961; k = ln(1,2) ) |
| |
| 3.2 | Berechnen Sie denjenigen Zeitpunkt t1, an dem die Keimzahl 5000 pro cm3 Milch beträgt. (2 BE) |
| |
| 3.3 | Durch zunehmendes Absterben der Keime verläuft die Keimzahl ab dem Zeitpunkt t2 = 5,19 h nach der Funktion b mit b( t ) = 1000·t·e–0,001 t2. Zeigen Sie, dass der Übergang der Funktionen a und b (im Rahmen der Rundungsgenauigkeit) stetig und differenzierbar erfolgt. (7 BE) |
| |
| 3.4 | Untersuchen Sie, zu welchem Zeitpunkt die Keimzahl ihren größten Wert erreicht und berechnen Sie diese Keimzahl. (4 BE) |
1 | Gegeben ist die Schar reeller Funktionen f : x : x 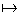 f f (x) = (x) = 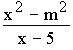 mit reellen, positiven Parameterwerten m und der Definitionsmenge ID mit reellen, positiven Parameterwerten m und der Definitionsmenge ID 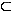 IR . IR . |
| |
| 1.1 | Bestimmen Sie die maximale Definitionsmenge IDm sowie jeweils in Abhängigkeit von m die Nullstellen, die Art der Definitionslücke und das Verhalten von fm(x) bei Annäherung an die Definitionslücke. (9 BE) |
| |
| 1.2 | Ermitteln Sie die Gleichungen aller Asymptoten der Graphen von fm. (4 BE) |
| |
| 1.3 | Untersuchen Sie, für welche Werte von m Extrempunkte des Graphen von fm existieren. (5 BE)
( Zur Kontrolle: f '(x) = '(x) = 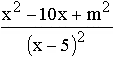 ) ) |
| 1.4 | Nun sei m = 4. Bestimmen Sie mit Hilfe der Ergebnisse aus Aufgabe 1.3 die Koordinaten und die Art der lokalen Extrempunkte des Graphen von f4 , und zeichnen Sie die Asymptoten und den Graphen anhand geeigneter Funktionswerte für –8 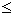 x x 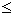 16 in ein kartesisches Koordinatensystem. (Maßstab auf beiden Achsen: 1LE = 0,5 cm; Platzbedarf beachten) (9 BE) 16 in ein kartesisches Koordinatensystem. (Maßstab auf beiden Achsen: 1LE = 0,5 cm; Platzbedarf beachten) (9 BE) |
| |
| 1.5 | Der Graph von f4 und die x-Achse schließen ein endliches Flächenstück ein. Berechnen Sie die Maßzahl des zugehörigen Flächeninhalts. (5 BE)
(Hinweis: Zerlegen Sie den Funktionsterm f4(x) durch Polynomdivision) |
| |
| |
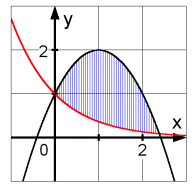
| 2 | In nebenstehendes Koordinatensystem sind der Graph der Exponentialfunktion g: x 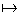 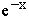 und die nach unten geöffnete Normalparabel mit Scheitelpunkt S(1|2) eingetragen. und die nach unten geöffnete Normalparabel mit Scheitelpunkt S(1|2) eingetragen. |
 |
| |
| 2.1 | Bestimmen Sie zunächst die rechte Schnittstelle beider Graphen unter Verwendung des Newton-Verfahrens näherungsweise (gerundet auf 3 Dezimalen), indem Sie mit dem Startwert x0 = 3 beginnen und zwei Iterationsschritte ausführen. (7 BE)
( Zur Kontrolle: Schnittstelle x2 = 2,385 ) |
| |
| 2.2 | Berechnen Sie den Inhalt der schraffierten Fläche auf drei Dezimalen. (4 BE) |
| |
| |
| 3 | Bei der Behandlung einer akuten Virusinfektion durch ein Medikament wird das folgende mathematische Modell zugrunde gelegt: Für die Virenkonzentration n (in Laboreinheiten) x Stunden nach der Medikamenteneinnahme gilt
n(x) = 20(2x + 1)e–0,5x mit x 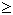 0. 0. |
| |
| 3.1 | Ermitteln Sie, in welchen Zeitintervallen nach der Einnahme des Medikaments die Virenkonzentration zunimmt bzw. abnimmt. Berechnen Sie die größte auftretende Virenkonzentration. (5 BE) |
| |
| 3.2 | Untersuchen Sie, wie sich die Einnahme des Medikaments langfristig auf die Virenkonzentration auswirkt, wenn obige Gleichung gilt. Verwenden Sie dazu die Regeln von L´Hospital. (3 BE) |
| |
| 3.3 | Zeigen Sie, dass 18 Stunden nach Einnahme des Medikaments die Nachweisgrenze von n0 = 0,1 Laboreinheiten unterschritten ist. (2 BE) |
| |
| 3.4 | Die Ableitungsfunktion n'(x) der Virenkonzentration hat für x 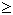 0 einen größten und einen kleinsten Wert. Bestimmen Sie diese beiden Werte n'(x0) und n'(x1). Erläutern Sie die Bedeutung des positiven der beiden x-Werte für den Verlauf des Graphen der Funktion n. (7 BE) 0 einen größten und einen kleinsten Wert. Bestimmen Sie diese beiden Werte n'(x0) und n'(x1). Erläutern Sie die Bedeutung des positiven der beiden x-Werte für den Verlauf des Graphen der Funktion n. (7 BE) |
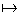 (2 – ln(x))·(2 + ln(x))
(2 – ln(x))·(2 + ln(x))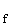
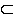 IR.
IR.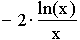 )
)
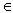 ] 0 ; 10 ] in ein kartesisches Koordinatensystem. (6 BE)
] 0 ; 10 ] in ein kartesisches Koordinatensystem. (6 BE)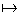 –x·(ln(x))2
+ bx·ln(x) + cx in IDf eine Stammfunktion von f ist, und berechnen Sie den Inhalt der endlichen Fläche, die der Graph von f mit der x-Achse einschließt. (10 BE)
–x·(ln(x))2
+ bx·ln(x) + cx in IDf eine Stammfunktion von f ist, und berechnen Sie den Inhalt der endlichen Fläche, die der Graph von f mit der x-Achse einschließt. (10 BE)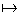 g(x) =
g(x) = 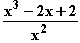 mit Definitionsmenge
mit Definitionsmenge  = ] 0 ; ∞ [
= ] 0 ; ∞ [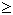 1 mit der Asymptoten und der Gerade x = 3 einschließt. (7 BE)
1 mit der Asymptoten und der Gerade x = 3 einschließt. (7 BE)
 : x
: x 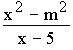 mit reellen, positiven Parameterwerten m und der Definitionsmenge ID
mit reellen, positiven Parameterwerten m und der Definitionsmenge ID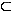 IR .
IR .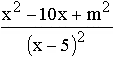 )
)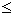 x
x 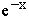 und die nach unten geöffnete Normalparabel mit Scheitelpunkt S(1|2) eingetragen.
und die nach unten geöffnete Normalparabel mit Scheitelpunkt S(1|2) eingetragen.