Abschlussprüfung zur Erlangung der fachgebundenen Hochschulreife
Frühjahr 2006

Aufgabengruppe A:   A I   A II


A I

1     

Gegeben ist die Funktion 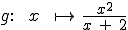   mit der maximalen Definitionsmenge D(g) . Der Graph von  g  heißt G(g)..
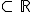Geben  Sie D(g) und die Nullstelle von  g  mit ihrer Vielfachheit an. Ermitteln Sie die Gleichungen aller Asymptoten des Graphen G(g) und skizzieren Sie den Graphen G(g) für 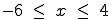   in ein kartesisches Koordinatensystem..   (10 BE)

 
 

2.0

Gegeben ist nun die Funktion 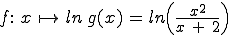   mit der maximalen Definitionsmenge  D(f) . Der Graph der Funktion  f  heißt G(f).

 

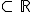2.1

Geben Sie D(f), das Verhalten von f(x)  für 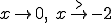   und für  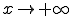 sowie die Gleichungen aller Asymptoten von G(f) an. Beachten Sie dabei die Eigenschaften der Funktion  g  aus Teilaufgabe 1.   (7 BE)

 

2.2

Berechnen Sie die Nullstellen der Funktion f.   (3 BE)

 

2.3

Ermitteln Sie rechnerisch die maximalen Intervalle, in denen die Funktion  f  echt monoton zunehmend bzw. echt monoton abnehmend ist.
(zur Kontrolle: 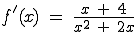 )    (7 BE)

 

2.4

Zeichnen Sie den Graphen G(f) und seine Asymptoten für  –2 < x ≤ 5  unter Verwendung der bisherigen Ergebnisse und nach der Berechnung weiterer geeigneter Funktionswerte in ein kartesisches Koordinatensystem.   (5 BE)

 
 
 

3.0

Bei der Herstellung von Keramiken werden Kammerbrennöfen verwendet. Die Brenntemperatur  B(t)  in °C eines Kammerbrennofens in Abhängigkeit von der Zeit  t  (0 ≤ t ≤ 13) in Stunden (h) kann durch folgende abschnittsweise definierte Funktion dargestellt werden: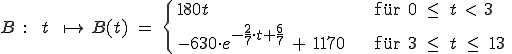 
    ,
wobei von Benennungen abgesehen wird.

 

3.1

Zeigen Sie, dass die Funktion  B  an der Stelle  t0 = 3  differenzierbar ist.   (6 BE)

 

3.2

Untersuchen Sie das Monotonieverhalten der Funktion  B.   (3 BE)

 

3.3

Der Kammerbrennofen erreicht 13 Stunden nach dem Beginn des Aufheizens seine maximale Brenntemperatur  Bmax . Zum Zeitpunkt  t1 liegt die Temperatur im Ofen 10 % unter Bmax . Berechnen Sie Bmax und den auf Stunden gerundeten Zeitpunkt  t1.   (5 BE)

 

3.4

Berechnen Sie den Wert 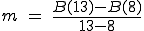  ,  geben Sie eine sinnvolle Einheit für  m  an, und interpretieren Sie  m  im gegebenen Zusammenhang.   (3 BE)

 

3.5

Zeichnen Sie unter Verwendung bisheriger Ergebnisse den Graphen der Funktion  B.
(Maßstab:  Abszissenachse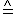: 1 cm 1 h;  Ordinatenachse: 1 cm 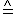100° C   (4 BE)

 

3.6

Die Maßzahl  W  des Flächeninhalts der Fläche zwischen dem Graphen von  B  und der  t-Achse lässt einen Rückschluss auf die aufgenommene Wärmemenge (Energie) für das Aufheizen des Brennofens bis zur Maximaltemperatur zu. Berechnen Sie die Maßzahl  W.   (7 BE)

 
 

 Lösungen zur Aufgabengruppe A I

 

A II


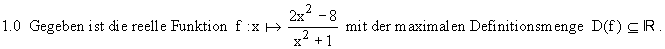       Der Graph von f wird mit G(f) bezeichnet .

1.1 Geben Sie D(f) an, bestimmen Sie die Nullstellen von f und untersuchen Sie G(f) auf Symmetrie .   (4 BE)

1.2 Bestimmen Sie die Gleichung der Asymptote sowie die Art und die Koordinaten des
      Extrempunktes von G(f) und geben Sie die Wertemenmge W(f) der Funktion f an .
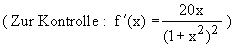                   (8 BE)

1.3 Berechnen Sie f(3) und f(6) und zeichnen Sie G(f) und seine Aysmptote für 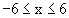 in ein kartesisches Koordinaten-
      system. (Ganze DIN A4-Seite verwenden, Ursprung in der Blattmitte, 1 LE = 1 cm)        (5 BE)


          Ihr Graph heißt G(g).

1.4.1 Ermitteln Sie D(g), die Nullstellen von g, die Gleichungen der Asymptoten sowie die Art und die
         Koordinaten des Extrempunktes von G(g). Beachten Sie dazu die Teilaufgaben 1.1 und 1.2 .  (6 BE)

1.4.2 Bestimmen Sie die Koordinaten der Schnittpunkte von G(f) und G(g).      (6 BE)

1.4.3 Zeichnen Sie G(g) und seine Asymptoten für 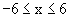 mit anderer Farbe in das Koordinatensystem
         von Teilaufgabe 1.3 .     (6 BE)


2.0 Auf einer Südseeinsel strandete Anfang Januar des Jahres 1955 ein Boot, wobei unter anderem auch
      Kaninchen an Bord waren . 32 Kaninchen überlebten und verwilderten auf der Insel . Für die Anzahl der
      Kaninchen in Abhängigkeit von der Zeit t in Jahren gilt näherungsweise die Funktion
       
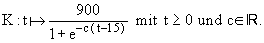      Die Zeit t wird ab dem 1.1.1955 gemessen .
      Im Funktionsterm und bei Berechnungen wird auf Benennungen verzichtet .

2.1 Bestimmen Sie den Wert von c .
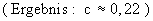                (4 BE)

2.2 Ermitteln Sie die Gleichung der Asymptote des Graphen von K und untersuchen Sie das
      Monotonieverhalten der Funktion K . Interpretieren Sie die Ergebnisse im Hinblick auf die Entwicklung
      der Kaninchenpopulation .
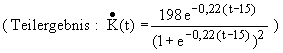            (7 BE)
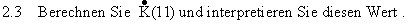     (3 BE)

2.4 Der Graph von K verläuft punktsymmetrisch zu seinem einzigen Wendepunkt .
      
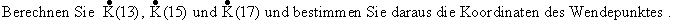      Erläutern Sie die Bedeutung des Wendepunktes für die Entwicklung der Kaninchenpopulation .  (6 BE)

2.5 Zeichnen Sie den Graphen von K und seine Asymptote für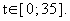 
      Berechnen Sie dazu K(t) für vier weitere sinnvolle Zeitpunkte .
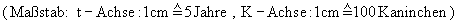        (5 BE)

 Lösungen zur Aufgabengruppe A II