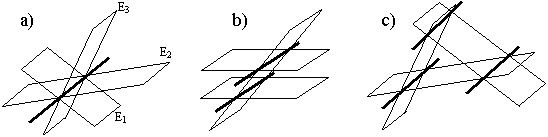
h
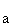 :
: 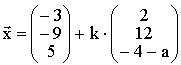 mit k
mit k 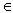 IR und a
IR und a 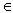 IR gegeben.
IR gegeben.Durch P und Q ist eine Gerade g festgelegt. Untersuchen Sie, ob eine Gerade ha parallel zu g verläuft. (4 BE)
Bestimmen Sie denjenigen Wert a, für den die zugehörige Gerade ha die Gerade g schneidet. Berechnen Sie auch die Koordinaten des Schnittpunktes S. (7 BE)
( Teilergebnis: S( –9 | –45 | 8 ) )
1.3
Berechnen Sie das Teilverhältnis λ aus der Gleichung 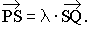 Erläutern Sie damit die Lage des Punktes S bezüglich der Punkte P und Q. (4 BE)
Erläutern Sie damit die Lage des Punktes S bezüglich der Punkte P und Q. (4 BE)
Die Ebene E enthält die Geraden g und h-3 (also a = –3). Ermitteln Sie eine Gleichung von E in Koordinatenform. (5 BE)
( Mögliches Ergebnis für E: 8x1 – x2 + 4x3 – 5 = 0 )
Geben Sie die Koordinaten je eines Punktes auf der x1x2-Koordinatenebene bzw. auf der x1x3-Koordinatenebene an, der gleichzeitig in E, aber nicht auf einer Koordinatenachse liegt. (4 BE)
Drei Firmen A, B und C sind nach dem Leontief-Modell miteinander verflochten. Die gegenseitig und für den Markt erbrachten Leistungen werden in Verrechnungseinheiten in folgender Tabelle zusammengestellt:
|
A |
B |
C |
Markt |
|
|
A |
0 |
60 |
8 |
332 |
|
B |
100 |
0 |
54 |
146 |
|
C |
80 |
48 |
0 |
72 |
Stellen Sie die Inputmatrix auf. Bestimmen Sie denjenigen Produktions-
vektor 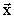 , der zum Nachfragevektor
, der zum Nachfragevektor 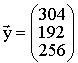 gehört. (8 BE)
gehört. (8 BE)
Im Vektorraum der Polynome vom Grad kleiner oder gleich 2 sind die Elemente
Begründen Sie, dass {p1, p2, p3} eine Basis des Vektorraums bildet. (4 BE)
Berechnen Sie die Koordinaten des Elements p4= 9x2 – 8x – 5 bezüglich dieser Basis. (4 BE)

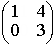 gegeben.
gegeben. sind die Ebene
sind die Ebene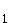 :
: 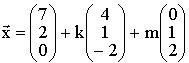 , sowie in Abhängigkeit von s
, sowie in Abhängigkeit von s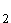 : 4x
: 4x – s = 0 und E
– s = 0 und E x
x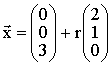 in E
in E