1.0
Im einem kartesischen Koordinatensystem des 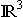 sind die Ebene E, die
jede Koordinatenachse bei +1 schneidet, und die Gerade
g:
sind die Ebene E, die
jede Koordinatenachse bei +1 schneidet, und die Gerade
g: 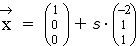 mit
mit 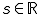 gegeben..
gegeben..
1.1
Bestimmen Sie eine vektorielle Gleichung von
E und geben Sie eine Koordinatengleichung von E
an.
(Mögliches Teilergebnis E: x1 +
x2 + x3 – 1 = 0) (3 BE)
1.2
Untersuchen Sie die Lage der Geraden g bezüglich der Ebene E. (2 BE)
1.3
Ermitteln Sie die Koordinaten des Schnittpunktes
S der Geraden g mit der
x2x3-Koordinatenebene.
Der Punkt T(1 | 0 |
0) ist der Mittelpunkt der Strecke [SR]. Berechnen Sie die
Koordinaten des Punktes R. (6 BE)
2.0
Die drei Wirtschaftssektoren U, V
und W sind nach dem Leontief-Modell miteinander und mit dem
Markt gemäß der Inputmatrix 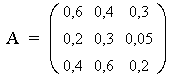 verflochten.
verflochten.
2.1
U stellt im betrachteten Produktionszeitraum 220 Mengeneinheiten (ME), V 80 ME und W 180 ME her. Stellen Sie die zugehörige Verflechtung tabellarisch dar. (5 BE)
2.2.0
Für den Marktabgabevektor gilt nun 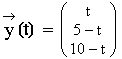 , wobei t
eine konjunkturabhängige Größe ist.
, wobei t
eine konjunkturabhängige Größe ist.
2.2.1
Bestimmen Sie die rellen Werte von t, für
welche der Marktabgabevektor 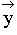 sinnvoll ist.
(2 BE)
sinnvoll ist.
(2 BE)
2.2.2
Bestimmen Sie den Produktionsvektor 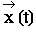 in Abhängigkeit
von t. (7 BE)
in Abhängigkeit
von t. (7 BE)
2.2.3
Ermitteln Sie den Wert von 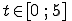 , für welchen die Summe p(t) der Produktionen
der drei Wirtschaftssektoren ein absolutes Minimum annimmt. Untersuchen
Sie, ob dann auch die Summe m(t) der Marktabgaben minimal
wird. (3 BE)
, für welchen die Summe p(t) der Produktionen
der drei Wirtschaftssektoren ein absolutes Minimum annimmt. Untersuchen
Sie, ob dann auch die Summe m(t) der Marktabgaben minimal
wird. (3 BE)
3.0
Beim „additiven RGB-Farbmodell“, das z. B. bei
Bildschirmfarben verwendet wird, lassen sich aus je 256 ganzzahligen Rot-,
Grün- und Blau-Farbwerten von 0 bis 255 genau 2563 =
16 777 216 Farbtöne gewinnen. Jeder dieser Farbtöne lässt sich
als ein Vektor darstellen, dessen Komponenten jeweils den Rot-, Grün- und
Blau-Anteil des Farbtons darstellen.
Es stehen die Farbtöne 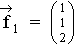 ,
, 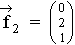 und
und 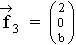 mit b
mit b 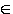 B, wobei B = {0 ; 1 ; ... ; 255}, zur
Verfügung. Aus
B, wobei B = {0 ; 1 ; ... ; 255}, zur
Verfügung. Aus 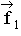 ,
, 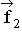 und
und 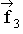 soll nun der Farbton
soll nun der Farbton 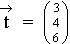 gemischt
werden, wobei sich der Farbton aus
gemischt
werden, wobei sich der Farbton aus 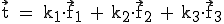 mit den rellen Mischungsfaktoren
mit den rellen Mischungsfaktoren 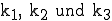 ergibt.
ergibt.
3.1
Zunächst sei b = 2. Zeigen Sie, dass für b = 2 die genannte Mischung auf genau eine Weise möglich ist, und geben Sie diese an. (6 BE)
3.2
Bestimmen Sie nun allgemein für die genannte Mischung den
nötigen Mischungsfaktor von 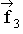 für b
für b 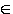 B \
{3}.
B \
{3}.
(Ergebnis: 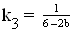 ) (3 BE)
) (3 BE)
3.3
Bei den RGB-Farbmischungen ist zu beachten, dass die
Mischungsfaktoren 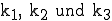 nicht negativ sein dürfen und die Farbtöne
nicht negativ sein dürfen und die Farbtöne 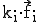 mit
mit 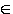 {1;2;3}
{1;2;3}
Untersuchen
Sie unter diesen Voraussetzungen anhand des Ergebnisses von Aufgabe 3.2,
ob die oben genannte Mischung auch für ein 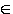 B \ {2;3}
B \ {2;3}

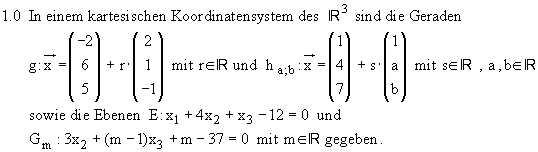 1.1 Geben Sie die besondere Lage der Geraden h 0; 0 ( also a = 0 , b = 0 ) bezüglich der Koordinatenebenen
an und berechnen Sie gegebenenfalls die Koordinaten der Schnittpunkte von h 0; 0 mit den Koordinatenebenen .
( 5 BE )
1.2 Ermitteln Sie die Werte der Parameter a und b, für welche die zugehörige Gerade h a; b und die Gerade g echt parallel
sind . ( 4 BE )
1.3 Für a = 0,5 und b = - 0,5 legen die zugehörige Gerade h a; b und die Gerade g eindeutig die Ebene F fest .
Ermitteln Sie je eine Gleichung der Ebene F in vektorieller und in parameterfreier Darstellung .
1.1 Geben Sie die besondere Lage der Geraden h 0; 0 ( also a = 0 , b = 0 ) bezüglich der Koordinatenebenen
an und berechnen Sie gegebenenfalls die Koordinaten der Schnittpunkte von h 0; 0 mit den Koordinatenebenen .
( 5 BE )
1.2 Ermitteln Sie die Werte der Parameter a und b, für welche die zugehörige Gerade h a; b und die Gerade g echt parallel
sind . ( 4 BE )
1.3 Für a = 0,5 und b = - 0,5 legen die zugehörige Gerade h a; b und die Gerade g eindeutig die Ebene F fest .
Ermitteln Sie je eine Gleichung der Ebene F in vektorieller und in parameterfreier Darstellung .
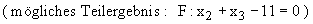 ( 4 BE )
1.4 Ermitteln Sie eine Gleichung der Schnittgeraden s der Ebenen E und F . ( 4 BE )
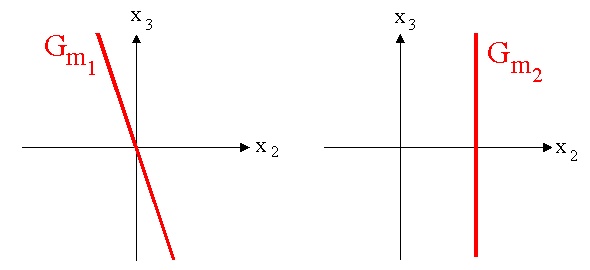
1.5 In der Zeichnung sind für zwei verschiedene m-Werte m1 und m2 die Schnittgeraden der Ebene Gm mit
der x2 x3 - Koordinatenebene dargestellt . Geben Sie die zugehörigen m-Werte an.
( Die Zeichnungen sind nicht maßstäblich ! )
( 4 BE )
1.4 Ermitteln Sie eine Gleichung der Schnittgeraden s der Ebenen E und F . ( 4 BE )
1.5 In der Zeichnung sind für zwei verschiedene m-Werte m1 und m2 die Schnittgeraden der Ebene Gm mit
der x2 x3 - Koordinatenebene dargestellt . Geben Sie die zugehörigen m-Werte an.
( Die Zeichnungen sind nicht maßstäblich ! )
 ( 3 BE )
1.6 Die Betrachtung des Schnittproblems der Ebenen E , F und Gm führt auf das folgende lineare Gleichungssystem :
( 3 BE )
1.6 Die Betrachtung des Schnittproblems der Ebenen E , F und Gm führt auf das folgende lineare Gleichungssystem :
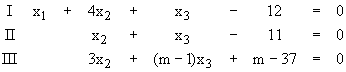 Ermitteln Sie in Abhängigkeit von m die Anzahl der Lösungen dieses Gleichungssystems und
interpretieren Sie Ihre Aussage jeweils im gegebenen Zusammenhang geometrisch . ( 6 BE )
2.0 Die Zweigwerke U, V und W eines Bergbauunternehmens bauen die Rohstoffe R1 , R2 und R3 ab .
Die Rohstoffe werden zum Teil an die weiterverarbeitende Industrie geliefert und zum Teil innerbetrieblich
verbraucht ( interner Verbrauch ) . U, V und W sind nach dem Leontief-Modell untereinander und mit der
weiterverarbeitenden Industrie durch die Inputmatrix
Ermitteln Sie in Abhängigkeit von m die Anzahl der Lösungen dieses Gleichungssystems und
interpretieren Sie Ihre Aussage jeweils im gegebenen Zusammenhang geometrisch . ( 6 BE )
2.0 Die Zweigwerke U, V und W eines Bergbauunternehmens bauen die Rohstoffe R1 , R2 und R3 ab .
Die Rohstoffe werden zum Teil an die weiterverarbeitende Industrie geliefert und zum Teil innerbetrieblich
verbraucht ( interner Verbrauch ) . U, V und W sind nach dem Leontief-Modell untereinander und mit der
weiterverarbeitenden Industrie durch die Inputmatrix
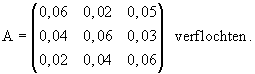 2.1 Erläutern Sie die Bedeutung der Werte 0,06 in der Hauptdiagonalen der Inputmatrix A . ( 2 BE )
2.2 Zweigwerk U gibt 704 ME , Zweigwerk V 796 ME und Zweigwerk W 512 ME an die weiterverarbeitende Industrie ab .
Ermitteln Sie, welche Mengen bei diesen externen Abgaben intern verbraucht werden . ( 7 BE )
2.1 Erläutern Sie die Bedeutung der Werte 0,06 in der Hauptdiagonalen der Inputmatrix A . ( 2 BE )
2.2 Zweigwerk U gibt 704 ME , Zweigwerk V 796 ME und Zweigwerk W 512 ME an die weiterverarbeitende Industrie ab .
Ermitteln Sie, welche Mengen bei diesen externen Abgaben intern verbraucht werden . ( 7 BE )
 Vom Endprodukt E1 sollen 295 ME , vom Endprodukt E2 35 ME und vom Endprodukt E3 80 ME hergestellt werden .
Bestätigen Sie, dass dazu vom Betrieb U 1000 ME , vom Betrieb V 1500 ME und vom Betrieb W 2000 ME abgebaut
werden müssen . ( 5 BE )
Vom Endprodukt E1 sollen 295 ME , vom Endprodukt E2 35 ME und vom Endprodukt E3 80 ME hergestellt werden .
Bestätigen Sie, dass dazu vom Betrieb U 1000 ME , vom Betrieb V 1500 ME und vom Betrieb W 2000 ME abgebaut
werden müssen . ( 5 BE )