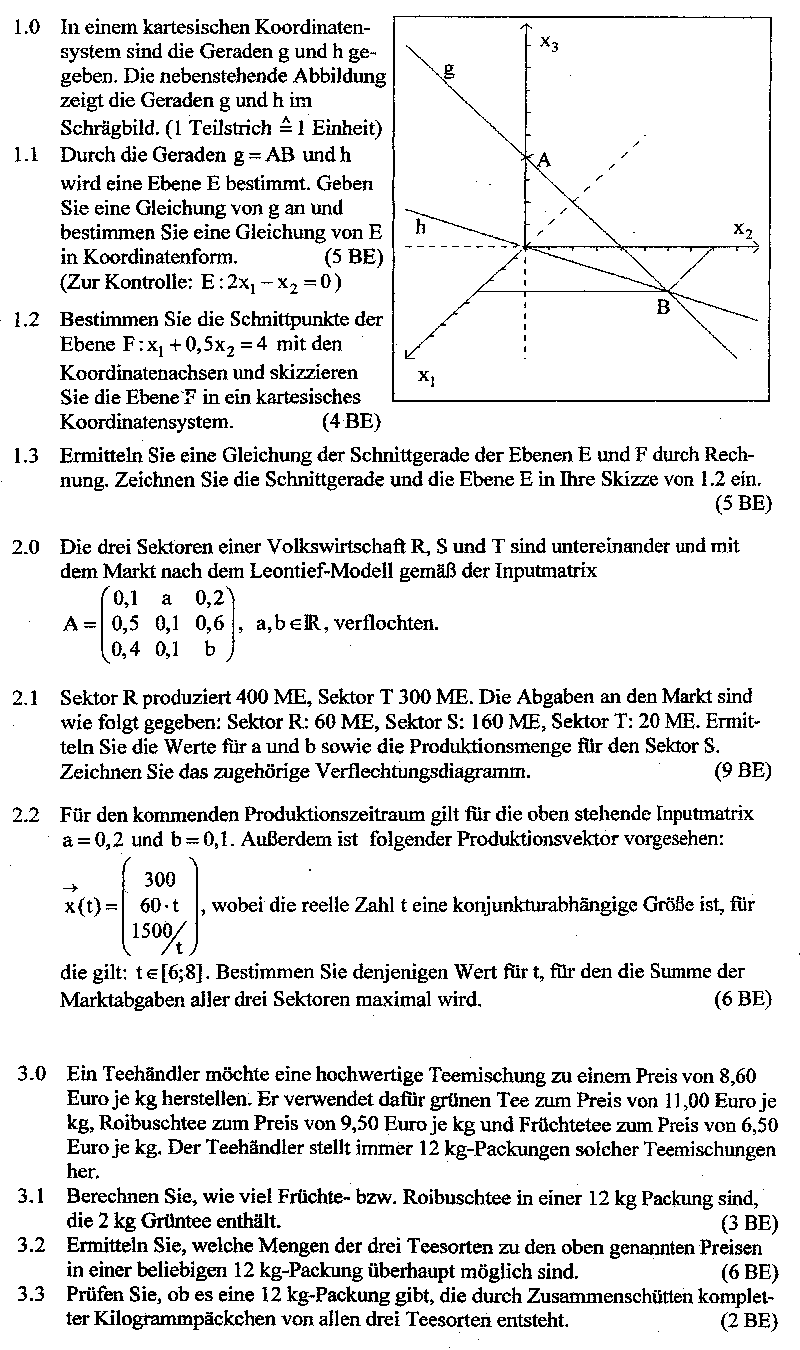
1.0     

In einem kartesischen Koordinatensystem sind die Punkte A(2 | 10 | 1), B(–1 | 13 | 4) und C(–8 | k | 7) mit kIR gegeben.

1.1

Stellen Sie fest, ob es Werte von k gibt, so dass A, B und C auf einer Geraden liegen.     (4 BE)

1.2

Die Ebene F wird durch die Punkte A, B und C (k = 2) aufgespannt.Bestimmen Sie je eine Gleichung von F in Parameter- und Koordinatenform.
(mögliches Ergebnis:  F: )     (5 BE)

1.3

Ermitteln Sie eine Gleichung der Schnittgeraden g zwischen der Ebene F und der -Koordinatenebene.     (3 BE)

1.4.0

Gegeben ist die Ebenenschar .

1.4.1

Prüfen Sie, ob die Ebene F zu der Ebenenschar E gehört.     (5 BE)

1.4.2

Bestimmen Sie die Anzahl der Achsenschnittpunkte der Ebenenschar E in Abhängigkeit von a.     (6 BE)

1.4.3

Untersuchen Sie die Lage der Geraden   zur Ebene E (also  a = 0).     (3 BE)

2.0

Die Zweigwerke U, V und W eines Unternehmens und der Markt sind nach dem Leontief-Modell verflochten.
Es gilt:  , wobei E die Einheitsmatrix und A die Inputmatrix ist.

2.1

Erstellen Sie eine Input-Output-Tabelle für den Produktionsvektor  .     (4 BE)

2.2

Aufgrund eines veränderten Nachfrageverhaltens ergibt sich folgende Situation:
•   Werk U gibt doppelt so viele Mengeneinheiten (ME) an den Markt ab wie das Werk V ;
•   Werk W gibt 7 ME an den Markt ab ;
•   die Gesamtproduktion im Werk W ist um 20 ME größer als im Werk U.
Bestimmen Sie den Produktionsvektor und den Marktvektor.     (7 BE)

2.3

Das Produkt von Werk V wird auf dem Markt nicht mehr nachgefragt. Die Marktabgabe von Werk V wird deshalb eingestellt. Bestimmen Sie, welche Menge in Werk V bei einer Produktion von 55 ME in U und 100 ME in W trotzdem noch produziert werden muss.     (3 BE)