a) x = lg 1000 = 3 b) x = lg 5 = 0,7 c) x = ln 54,6 = 4
d) x = ln 0,05 = –3 e) x = 5
f) 2x = e  (eln 2)x = e
(eln 2)x = e  e(ln 2) ·x = e
e(ln 2) ·x = e
 (ln 2) ·x = ln e = 1
(ln 2) ·x = ln e = 1  x =
x =  = 1,44
= 1,44
2.
a) ln e =  = 1 b)
= 1 b) 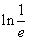 =
=  = –1
= –1
c) 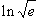 =
=  =
=  d)
d) 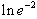 = –2
= –2
e) 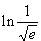 =
=  = –
= – f)
f) 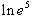 = 5
= 5
g)  =
=  ·2 = 2
·2 = 2 h)
h) 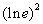 = (
= ( )² = 1² = 1
)² = 1² = 1
i) 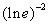 = (
= ( )
) = 1
= 1 =
=  = 1
= 1
j) 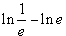 =
=  –
–  = –1 – 1 = –2
= –1 – 1 = –2
3.
a) 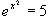
 x
x = ln 5
= ln 5  x
x

 =
= 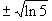
b) 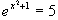
 x
x +1 = ln 5
+1 = ln 5  x
x = –1+ln 5
= –1+ln 5  x
x

 =
= 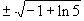
c) 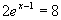


 x – 1 = ln 4
x – 1 = ln 4  x = 1 + ln 4
x = 1 + ln 4
d) 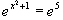
 x
x + 1 = 5
+ 1 = 5  x
x = 4
= 4  x
x

 = ±2
= ±2
e) 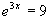
 3x = ln 9
3x = ln 9  x =
x = 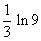
f) 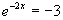 : keine Lösung, da ln(–3) nicht definiert!
: keine Lösung, da ln(–3) nicht definiert!
g) 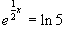

 x = ln(ln 5)
x = ln(ln 5)  x = 2 ln(ln 5)
x = 2 ln(ln 5)
h) 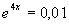
 4x = ln 0,01
4x = ln 0,01  x =
x =  ln 0,01
ln 0,01
i) 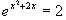
 x
x + 2x = ln 2
+ 2x = ln 2  x
x + 2x – ln 2 = 0
+ 2x – ln 2 = 0
D = 4 + 4 ln 2 > 0 
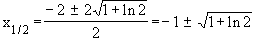
j) 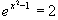
 x
x –1 = ln 2
–1 = ln 2  x
x = 1+ln 2
= 1+ln 2  x
x

 =
= 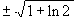
k) 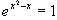
 x
x –x = ln 1 = 0
–x = ln 1 = 0  x(x–1) = 0
x(x–1) = 0  x
x = 0; x
= 0; x = 1
= 1
4.
a) 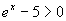


 x > ln 5
x > ln 5
b) 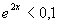
 2x < ln 0,1
2x < ln 0,1  x <
x <  ln 0,1
ln 0,1
c) 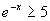
 –x ≥ ln 5
–x ≥ ln 5  x ≤ –ln 5
x ≤ –ln 5
d) 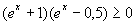

| ex + 1 ≥ 0 |  | ex – 0,5 ≥ 0 |  | ex + 1 ≤ 0 |  | ex – 0,5 ≤ 0 |
| ex ≥ –1 |  | ex ≥ 0,5 |  | ex ≤ –1 |  | ex ≤ 0,5 |
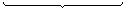 ex ≥ 0,5 | 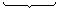 keine Lösung | |||||
 ex ≥ 0,5
ex ≥ 0,5  x ≥ ln 0,5
x ≥ ln 0,5
e) 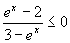

| ex – 2 ≥ 0 |  | 3 – ex < 0 |  | ex – 2 ≤ 0 |  | 3 – ex > 0 |
| ex ≥ 2 |  | ex > 3 |  | ex ≤ 2 |  | ex < 3 |
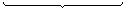 ex > 3 |  | 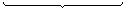 ex ≤ 2 |
||||
 x > ln 3
x > ln 3  x ≤ ln 2
x ≤ ln 2
f) 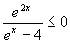

| e2x ≥ 0 |  | ex – 4 < 0 |  | e2x ≤ 0 |  | ex – 4 > 0 |
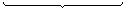 ex < 4 | 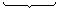 keine Lösung | |||||
 x < ln 4
x < ln 4
5.1
a) 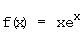 Definitionsgrenzen: –∞; +∞
Definitionsgrenzen: –∞; +∞
x  –∞
–∞  ex
ex  0
0  Fall für de L'Hospital:
Fall für de L'Hospital:
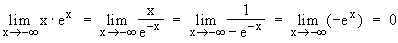
x  +∞
+∞  ex
ex  +∞
+∞  x·ex
x·ex  +∞
+∞
b) 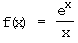 Definitionsgrenzen: –∞; 0; +∞
Definitionsgrenzen: –∞; 0; +∞
x  –∞
–∞  e
e
 0
0 
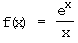
 0
0
x  0
0  e
e
 1
1 
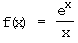

 ∞
∞
x  +∞
+∞  ex
ex  +∞
+∞  Fall für de L'Hospital:
Fall für de L'Hospital:
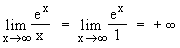
c) 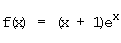 Definitionsgrenzen: –∞; +∞
Definitionsgrenzen: –∞; +∞
x  –∞
–∞  x + 1
x + 1  –∞
–∞  ex
ex  0
0  Fall für de L'Hospital:
Fall für de L'Hospital:
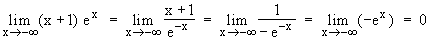
x  +∞
+∞  ex
ex  +∞
+∞  (x + 1)·ex
(x + 1)·ex  +∞.
+∞.
d) 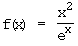 Definitionsgrenzen: –∞; +∞
Definitionsgrenzen: –∞; +∞
x  –∞
–∞  x
x
 +∞
+∞  e
e
 0
0 
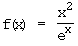
 +∞
+∞
x  +∞
+∞  x
x
 +∞
+∞  e
e
 +∞
+∞  Fall für de L'Hospital:
Fall für de L'Hospital:
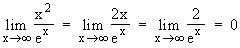
e) 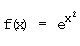 Definitionsgrenzen: –∞; +∞
Definitionsgrenzen: –∞; +∞
x 
 ∞
∞  x
x
 +∞
+∞ 
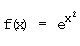
 +∞
+∞
f) 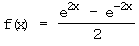 Definitionsgrenzen: –∞; +∞
Definitionsgrenzen: –∞; +∞
x  –∞
–∞  e
e

 0
0  e
e


 +∞
+∞  f(x)
f(x)  –∞
–∞
g) 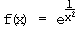 Definitionsgrenzen: –∞; 0; +∞
Definitionsgrenzen: –∞; 0; +∞
x 
 ∞
∞ 

 0
0 
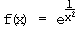
 1
1
x  0
0 

 +∞
+∞ 
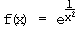
 +∞
+∞
h) 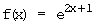 Definitionsgrenzen: –∞; +∞
Definitionsgrenzen: –∞; +∞
x  –∞
–∞  2x +1
2x +1  –∞
–∞ 
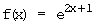
 0
0
x  +∞
+∞  2x +1
2x +1  +∞
+∞ 
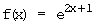
 +∞
+∞
i) 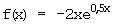 Definitionsgrenzen: –∞; +∞
Definitionsgrenzen: –∞; +∞
x  –∞
–∞  –2x
–2x  +∞
+∞  e0,5x
e0,5x  0
0  Fall für de L'Hospital:
Fall für de L'Hospital:
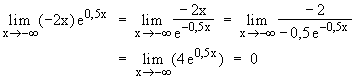
x  +∞
+∞  –2x
–2x  –∞
–∞  e0,5x
e0,5x  +∞
+∞  –2x·e0,5x
–2x·e0,5x  –∞
–∞
j) 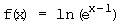 Definitionsgrenzen: –∞; +∞
Definitionsgrenzen: –∞; +∞
x 
 ∞
∞ 
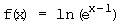 = x – 1
= x – 1 
 ∞
∞
k) 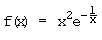 Definitionsgrenzen: –∞; 0; +∞
Definitionsgrenzen: –∞; 0; +∞
x 
 ∞
∞  x
x
 +∞
+∞ 
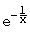
 1
1 
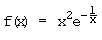
 +∞
+∞
x  0
0  x
x
 0
0 
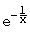
 +∞
+∞  Fall für de L'Hospital:
Fall für de L'Hospital:
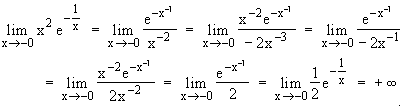
x  0
0  x
x
 0
0 
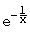
 0
0 
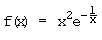
 0
0
5.2
a) 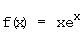
 f '(x) =
f '(x) = 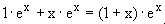
b) 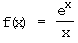
 f '(x) =
f '(x) = 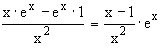
c) 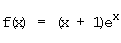
 f '(x) =
f '(x) = 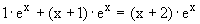
d) 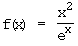
 f '(x) =
f '(x) = 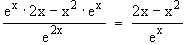
e) 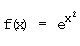
 f '(x) =
f '(x) = 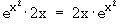
f) 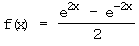
 f '(x) =
f '(x) = 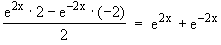
g) 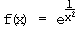
 f '(x) =
f '(x) = 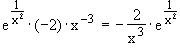
h) 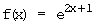
 f '(x) =
f '(x) = 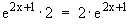
i) 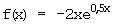
 f '(x) =
f '(x) = 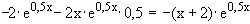
j) 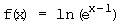 = x – 1
= x – 1  f '(x) = 1
f '(x) = 1
k) 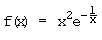
 f '(x) =
f '(x) = 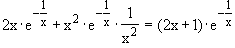
6.1
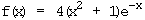
Symmetrie: f(–x) = 4[(–x)² + 1]·ex = 4(x² + 1)·ex ≠ ± f(x)
 keine Symmetrie
keine Symmetrie
Verhalten von f(x) für x  ±∞:
±∞:
x  –∞
–∞  x2 + 1
x2 + 1  +∞
+∞  e–x
e–x  +∞
+∞  f(x)
f(x)  +∞
+∞
x  +∞
+∞  x2 + 1
x2 + 1  +∞
+∞  e–x
e–x  0
0  Fall für de L'Hospital:
Fall für de L'Hospital:
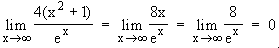
Nullstellen von f:
x2 + 1 = 0: keine Lösung, also keine Nullstellen.
Extremwerte von f:
f '(x) = 4[2x·e–x + (x2 + 1)·e–x·(–1)] = –4(x2 – 2x + 1)·e–x = 0
 x1/2 = 1 ist doppelte Horizontalstelle, also Terrassenstelle von f
x1/2 = 1 ist doppelte Horizontalstelle, also Terrassenstelle von f
 TEP(1|
TEP(1| ). Daraus und aus dem Verhalten von f für x
). Daraus und aus dem Verhalten von f für x  ±∞ folgt,
±∞ folgt,
dass Gf in ganz IR echt monoton fällt.
Wendepunkte:
f ''(x) = –4[(2x – 2)·e–x – (x2 – 2x + 1)·e–x] = 4(x2 – 4x + 3)·e–x = 0
 x
x = 1; x
= 1; x = 3 sind einfache Flachstellen
= 3 sind einfache Flachstellen
 WEP
WEP (1|
(1| ) = TEP; WEP
) = TEP; WEP (3|
(3| )
)
Aus dem Zusammenhang ergibt sich, dass Gf für
6.2
Graf von f:
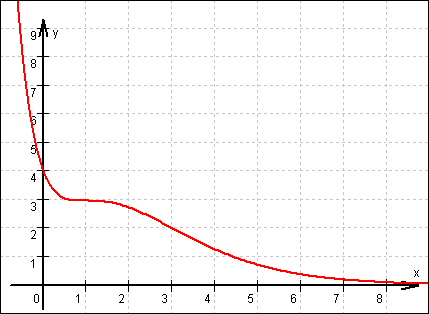
6.3
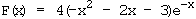

F'(x) = 4 [(–2x – 2)·e–x + (–x2 – 2x – 3)·e–x·(–1)]
= 4 (x2 + 1)·e–x = f(x) 
F ist eine Stammfunktion von f.
Berechnung der Fläche A(c) zwischen Gf und der x-Achse in den Grenzen
A(c) = 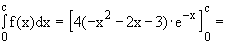
 + 12
+ 12
Grenzwert des Terms  für
für  ∞
∞
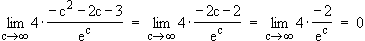
 Für c
Für c  ∞ gilt: A(c)
∞ gilt: A(c)  12
12

 und der x-Achse im 1. Quadranten beträgt
und der x-Achse im 1. Quadranten beträgt
12 FE.
7.1
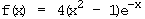
Symmetrie: f(–x) = 4[(–x)² – 1]·ex = 4(x² – 1)·ex ≠ ± f(x)
 keine Symmetrie
keine Symmetrie
Verhalten von f(x) für x  ±∞:
±∞:
x  –∞
–∞  x2 – 1
x2 – 1  +∞
+∞  e–x
e–x  +∞
+∞  f(x)
f(x)  +∞
+∞
x  +∞
+∞  x2 – 1
x2 – 1  +∞
+∞  e–x
e–x  0
0  Fall für de L'Hospital:
Fall für de L'Hospital:
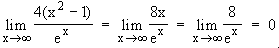
Nullstellen von f:
x2 – 1 = 0  x2 = 1
x2 = 1  x1/2 = ±1
x1/2 = ±1
Extremwerte von f:
f '(x) = 4[2x·e–x + (x2 – 1)·e–x·(–1)] = –4(x2 – 2x – 1)·e–x = 0

 sind einfache Horizontalstellen, also Extremstellen von f.
sind einfache Horizontalstellen, also Extremstellen von f.
Art und Lage der Extrempunkte:
f ''(x) = –4[(2x – 2)·e–x – (x2 – 2x – 1)·e–x] = 4(x2 – 4x + 1)·e–x
f ''( ) ≈ 17,12 > 0
) ≈ 17,12 > 0  TIP(
TIP( |–5)
|–5)
f ''( ) ≈ –1,01 < 0
) ≈ –1,01 < 0  HOP(
HOP( |1,73)
|1,73)
Wendepunkte:
f ''(x) = 4(x2 – 4x + 1)·e–x = 0

 sind einfache Flachstellen
sind einfache Flachstellen
 WEP
WEP (
( |–2,84); WEP
|–2,84); WEP (
( |1,24)
|1,24)
Aus dem Zusammenhang ergibt sich, dass G für
für 
 < x <
< x < 

7.2
Graf von f:
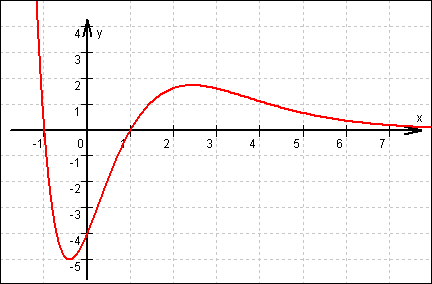
7.3
F(x) = (ax2 + bx + c)e–x 
F'(x) = (2ax + b)·e–x + (ax2 + bx + c)e–x(–1)
= [–ax2 + (2a – b)x + (b – c)]e–x = f(x) = (4x2 – 4)e–x 
Koeffizientenvergleich: I. –a = 4  a = –4
a = –4
II. 2a – b = 0  b = 2a = –8
b = 2a = –8
III. b – c = –4  c1 = b + 4 = –4
c1 = b + 4 = –4
Berechnung der Fläche A(c) zwischen Gf und der x-Achse in den Grenzen
A(c) = 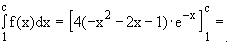
 +
+ 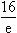
Grenzwert des Terms  für
für  ∞
∞
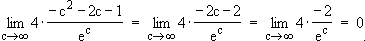
 Für c
Für c  ∞ gilt: A(c)
∞ gilt: A(c) 
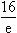

 und der x-Achse im 1. Quadranten beträgt
und der x-Achse im 1. Quadranten beträgt
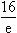 FE.
FE.
8.1
f(x) = e2x – 2ex = ex(ex – 2)
Symmetrie: f(–x) = e–2x – 2e–x ≠ ± f(x)
 keine Symmetrie
keine Symmetrie
Verhalten von f(x) für x  ±∞:
±∞:
x  –∞
–∞  ex
ex  0
0  ex – 2
ex – 2  –2
–2  f(x)
f(x)  0
0
x  +∞
+∞  ex
ex  +∞
+∞  ex – 2
ex – 2  +∞
+∞  f(x)
f(x)  +∞
+∞
Nullstelle von f:
ex – 2 = 0  ex = 2
ex = 2  x = ln 2
x = ln 2
Extremwerte von f:
f '(x) = e2x·2 – 2ex = 2ex(ex – 1) = 0
 ex = 1
ex = 1  x = ln 1 = 0 ist einfache Horizontalstelle, also Extremstelle von f.
x = ln 1 = 0 ist einfache Horizontalstelle, also Extremstelle von f.
Art und Lage des Extrempunktes:
f ''(x) = 2e2x·2 – 2ex = 4e2x – 2ex
f ''(0) = 2 > 0  TIP(0|–1)
TIP(0|–1)
Wendepunkte:
f ''(x) = 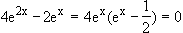

 ist eine einfache Flachstelle, also Wendestelle
ist eine einfache Flachstelle, also Wendestelle
 WEP(
WEP( |
| )
)
8.2
Graf von f:
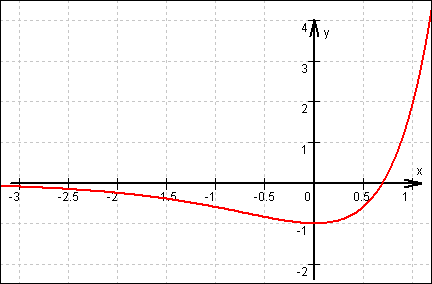
8.3
F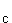 (x) = ∫ f(x)dx = ∫(e2x – 2ex)dx =
(x) = ∫ f(x)dx = ∫(e2x – 2ex)dx =  e2x – 2ex + c, c
e2x – 2ex + c, c 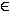 IR
IR
Gf  Graf von Fc :
Graf von Fc :
e2x – 2ex =  e2x – 2ex + c
e2x – 2ex + c 
 e2x = c
e2x = c  e2x = 2c
e2x = 2c
Diese Gleichung ist genau dann lösbar, wenn c > 0 
Für c > 0 schneiden sich die Grafen von f und Fc.
8.4
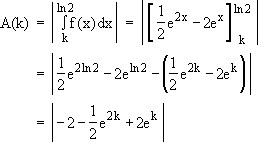
k  –∞
–∞ 

 0
0
 A(k)
A(k)  2
2
9.1
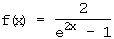
Definitionsbereich:
e2x – 1 = 0  e2x = 1
e2x = 1  2x = ln 1 = 0
2x = ln 1 = 0  x = 0
x = 0
 IDf = IR \ {0}
IDf = IR \ {0}
Asymptoten:
x  –∞
–∞  e2x – 1
e2x – 1  -1
-1  f(x)
f(x)  –2
–2
 waagrechte Asymptote links: y = –2
waagrechte Asymptote links: y = –2
x  ∞
∞  e2x – 1
e2x – 1  ∞
∞  f(x)
f(x)  0
0
 waagrechte Asymptote rechts: y = 0
waagrechte Asymptote rechts: y = 0
x  0
0  f(x)
f(x) 
 ∞
∞
 senkrechte Asymptote: x = 0
senkrechte Asymptote: x = 0
9.2
f '(x) =  : keine Lösung
: keine Lösung
 Gf hat keine Horizontalpunkte.
Gf hat keine Horizontalpunkte.
(f '(x) < 0 für alle x 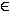 IDf
IDf  f fällt in seinem ganzen Definitionsbereich echt monoton.)
f fällt in seinem ganzen Definitionsbereich echt monoton.)
9.3
Graf von f:
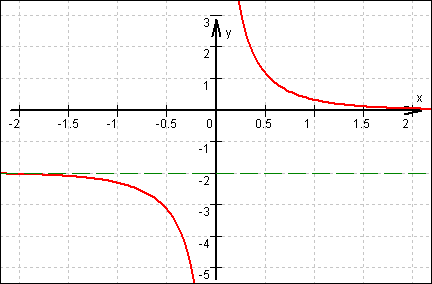
9.4
Gf ist punktsymmetrisch bezüglich Z(0|–1).
Beweis:
Die Behauptung gilt genau dann, wenn der um 1 nach oben verschobene Graf punktsymmetrisch bezüglich O ist.
Verschiebung von Gf um 1 nach oben ergibt den Grafen von g:
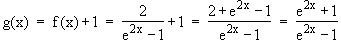
Anwendung des Kriteriums für Punktsymmetrie bzgl. O:
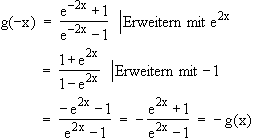
 Gg ist punktsymmetrisch bzgl. O, was zu zeigen war.
Gg ist punktsymmetrisch bzgl. O, was zu zeigen war.
9.5
Bestimmung von xP:
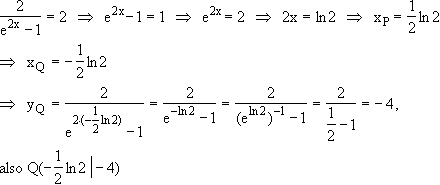
10.1
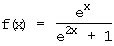
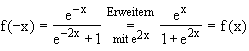
 Gf ist symmetrisch bzgl. der y-Achse.
Gf ist symmetrisch bzgl. der y-Achse.
10.2
Untersuchung auf Definitionslücken:
e2x + 1 = 0  e2x = –1
e2x = –1  2x = ln(–1): nicht definiert!
2x = ln(–1): nicht definiert!
 keine Definitionslücken
keine Definitionslücken  Definitionsgrenzen: ± ∞
Definitionsgrenzen: ± ∞
x  –∞
–∞  ex
ex  0
0  e2x + 1
e2x + 1  1
1  f(x)
f(x)  0
0
x  +∞
+∞  ex
ex  +∞
+∞  e2x + 1
e2x + 1  +∞
+∞  Fall für de L'Hospital:
Fall für de L'Hospital:
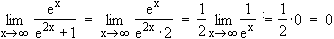
10.3
Monotonieverhalten:
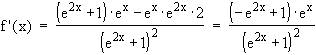
f '(x) = 0  –e2x + 1 = 0
–e2x + 1 = 0  e2x = 1
e2x = 1  2x = ln 1 = 0
2x = ln 1 = 0  x = 0
x = 0
Monotonietabelle von f:
| x < | 0 | < x | |
| Zähler der Ableitungsfkt. | + | 0 | – |
| Nenner der Ableitungsfkt. | + | + | + |
| Steigung | + | 0 | – |
| Graph | steigt | HOP(0| ) ) | fällt |
Wegen des Verhaltens für x
 ± ∞ und wegen der Tatsache, dass für alle
± ∞ und wegen der Tatsache, dass für alle 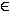 IR
IR  ).
). Für x < 0 steigt und für x > 0 fällt f echt monoton.
Für x < 0 steigt und für x > 0 fällt f echt monoton.
Krümmungsverhalten:
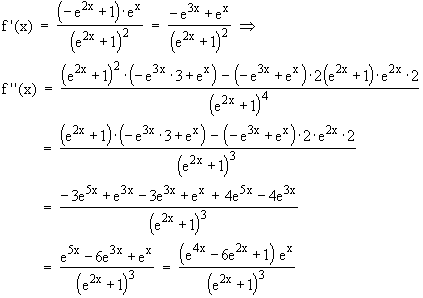
f ''(x) = 0  e4x – 6e2x + 1 = 0
e4x – 6e2x + 1 = 0  (e2x)2 – 6e2x + 1 = 0
(e2x)2 – 6e2x + 1 = 0
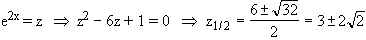

 ≈ 0,1716
≈ 0,1716 
 ≈ 5,8284
≈ 5,8284
 2x = ln 0,1716 = –1,76
2x = ln 0,1716 = –1,76  2x = ln 5,8284 = 1,76
2x = ln 5,8284 = 1,76
 x = –0,88
x = –0,88  x = 0,88
x = 0,88
Krümmungstabelle von f:
| x < | –0,88 | < x < | 0,88 | < x | |
| Zähler von f '' | + | 0 | – | 0 | + |
| Nenner von f '' | + | + | + | + | + |
| f ''(x) | + | 0 | – | 0 | + |
| Steigung | steigt | Max. | fällt | Min. | steigt |
| Graph | Links- kurve | WEP (–0,88 | 0,35) | Rechts- kurve | WEP (0,88 | 0,35) | Links- kurve |
Es handelt sich um zwei einfache Flachstellen von f.
 WEP1/2(±0,88 | 0,35)
WEP1/2(±0,88 | 0,35) Wegen des Verhaltens für x
 ± ∞ und wegen der Tatsache, dass bei
± ∞ und wegen der Tatsache, dass bei Für x < –0,88 sowie für x > 0,88 ist der Graf von f linksgekrümmt und für
10.4
Graf von f:
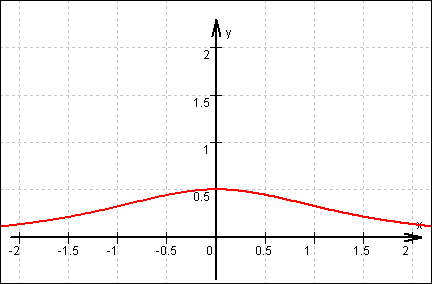
10.5
Waagrechte Asymptote y = 0  Zählergrad < Nennergrad;
Zählergrad < Nennergrad;
Gg symmetrisch bzgl. der y-Achse  z(x) = 1; n(x) = ax2 + c
z(x) = 1; n(x) = ax2 + c
g(0) = f(0) = 
 c = 2
c = 2
z. B. g(1) = f(1) = 0,324 
 = 0,324
= 0,324  a = 1,086 ,
a = 1,086 ,
also z. B.: g(x) = 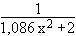
Graf von g:
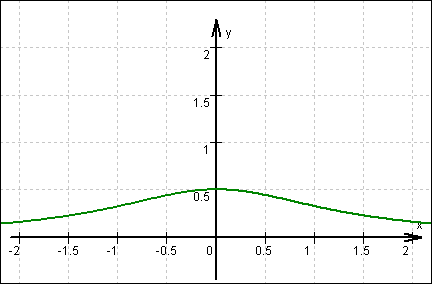
Zum Vergleich:
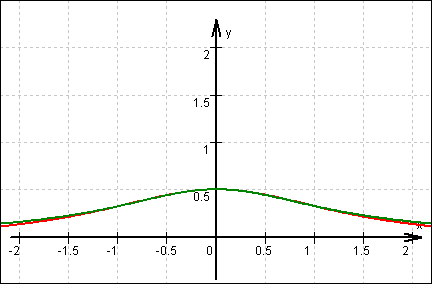
11.1
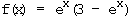
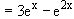
Symmetrie: f(–x) = 3e–x – e–2x ≠ ± f(x)
 keine Symmetrie
keine Symmetrie
Verhalten von f(x) für x  ±∞:
±∞:
x  –∞
–∞  ex
ex  0
0  3 – ex
3 – ex  3
3  f(x)
f(x)  0
0
x  +∞
+∞  ex
ex  +∞
+∞  3 – ex
3 – ex  –∞
–∞  f(x)
f(x)  –∞
–∞
Nullstelle von f:
3 – ex = 0  ex = 3
ex = 3  x = ln 3
x = ln 3
Extremwerte von f:
f '(x) = 3ex – e2x·2 = ex(3 – 2ex) = 0
 ex = 1,5
ex = 1,5  x = ln 1,5 ist einfache Horizontalstelle, also Extremstelle von f.
x = ln 1,5 ist einfache Horizontalstelle, also Extremstelle von f.
Art und Lage des Extrempunktes:
f ''(x) = 3ex – 2e2x·2 = 3ex – 4e2x
f ''(ln 1,5) = 3eln 1,5 – 4e2 ln 1,5 = 4,5 – 9 = –4,5 < 0
 HOP(ln 1,5 | 2,25)
HOP(ln 1,5 | 2,25)
Wendepunkte:
f ''(x) = 3ex – 4e2x = ex(3 – 4ex) = 0
 ex =
ex = 
 x = ln
x = ln  ist eine einfache Flachstelle, also Wendestelle von f
ist eine einfache Flachstelle, also Wendestelle von f
 WEP(ln
WEP(ln  |
|  )
)
11.2
Graf von f:
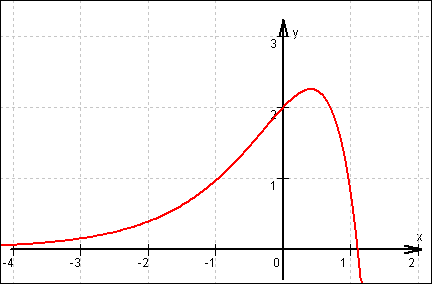
11.3
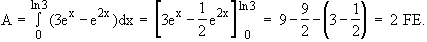
11.4
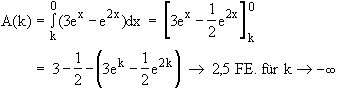
12.1
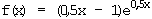
Nullstelle von f:
0,5x – 1 = 0  x = 2
x = 2
Verhalten von f(x) für x  ±∞:
±∞:
x  –∞
–∞  0,5x – 1
0,5x – 1  –∞
–∞  e0,5x
e0,5x  0
0  Fall für de L'Hospital:
Fall für de L'Hospital:
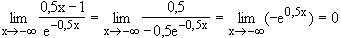
x  +∞
+∞  0,5x – 1
0,5x – 1  +∞
+∞  e0,5x
e0,5x  +∞
+∞  f(x)
f(x)  +∞
+∞
 –∞ folgt die waagrechte Asymptote
–∞ folgt die waagrechte Asymptote
Extremwerte:
f '(x) = 0,5·e0,5x + (0,5x – 1)·e0,5x·0,5 = 0,25x·e0,5x = 0  x = 0
x = 0
f ''(x) = 0,25·e0,5x + 0,25x·e0,5x·0,5 = (0,125x + 0,25)·e0,5x
f ''(0) = 0,25·e0 = 0,25 > 0  TIP(0 | –1)
TIP(0 | –1)
12.2
Graf von f:
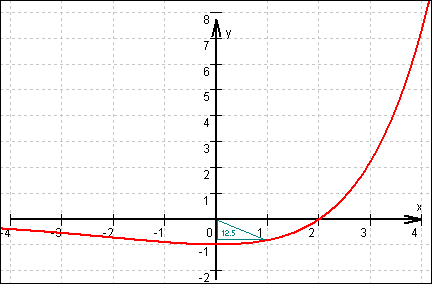
12.3
F(x) = (ax + b)e0,5x 
F'(x) = ae0,5x + (ax + b)e0,5x·0,5 = (0,5ax + a + 0,5b)e0,5x;
f(x) = (0,5x – 1)e0,5x; F'(x) = f(x)  Koeffizientenvergleich:
Koeffizientenvergleich:
I. 0,5a = 0,5  a = 1
a = 1
II. a + 0,5b = –1  1 + 0,5b = –1
1 + 0,5b = –1  b = –4
b = –4
12.4
Sei c < 0 
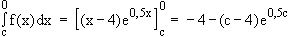
c  –∞
–∞  (c – 4)e0,5c
(c – 4)e0,5c  0, denn wegen
0, denn wegen  –∞
–∞ 0
0
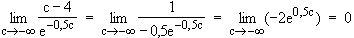
Also gilt für c  –∞:
–∞: 
 –4
–4 
Das beschriebene Flächenstück hat einen endlichen Inhalt, nämlich 4 FE.
12.5
A(a) =  g·h =
g·h =  a·[–f(a)] = (–0,25a2 + 0,5a)·e0,5a, IDA = ]0 ; 2[.
a·[–f(a)] = (–0,25a2 + 0,5a)·e0,5a, IDA = ]0 ; 2[.
A'(a) = (–0,5a + 0,5)·e0,5a + (–0,25a2 + 0,5a)·e0,5a·0,5
= (–0,125a2 – 0,25a + 0,5)e0,5a
= –0,125(a2 + 2a – 4)e0,5a
A'(a) = 0 
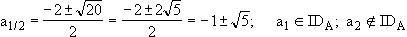
A''(a) = –0,125(2a + 2)e0,5a – 0,125(a2 + 2a – 4)e0,5a·0,5
= –0,0625(a2 + 6a + 4)e0,5a 
A''(a1) = –1,5 < 0 
Für  wird die Dreiecksfläche maximal.
wird die Dreiecksfläche maximal.
13.1
Nullstellen von f:
1. Fall: x < 2  f(x) = (0,5x – 1)e0,5x
f(x) = (0,5x – 1)e0,5x
0,5x – 1 = 0  x = 2: erfüllt nicht die Fallbedingung
x = 2: erfüllt nicht die Fallbedingung
 Für x < 2 existieren keine Nullstellen.
Für x < 2 existieren keine Nullstellen.
2. Fall: x ≥ 2  f(x) = –0,25x2 + 2x – 3
f(x) = –0,25x2 + 2x – 3
x – 8x + 12 = 0
– 8x + 12 = 0 
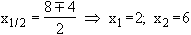
Extremwerte von f:
1. Fall: x < 2  f(x) = (0,5x – 1)e0,5x
f(x) = (0,5x – 1)e0,5x
 TIP(0 | –1): Begründung siehe Lösung zu Aufgabe 12.1
TIP(0 | –1): Begründung siehe Lösung zu Aufgabe 12.1
2. Fall: x > 2  f(x) = –0,25x2 + 2x – 3
f(x) = –0,25x2 + 2x – 3
 f '(x) = –0,5x + 2 = 0
f '(x) = –0,5x + 2 = 0  x = 4
x = 4
f ''(x) = –0,5 < 0  HOP(4 | 1)
HOP(4 | 1)
3. Fall: x = 2
x  2
2  f '(x) =
f '(x) = 
 0,5e > 0;
0,5e > 0;
x  2
2  f '(x) = –0,5x + 2
f '(x) = –0,5x + 2  1 > 0
1 > 0
Da beide Steigungsgrenzwerte > 0, gibt es bei x = 2 kein
Randwertextremum.
13.2
Stetigkeit bei x = 2:
x  2
2 
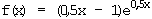
 0;
0;
f(2) = –0,25·22 + 2·2 – 3 = 0 
Da bei x = 2 der linksseitige Grenzwert der Funktion f mit ihrem dortigen Wert übereinstimmt, ist f dort stetig.
Differenzierbarkeit bei x = 2:
x  2
2  f '(x) =
f '(x) = 
 0,5e;
0,5e;
x  2
2  f '(x) = –0,5x + 2
f '(x) = –0,5x + 2  1
1 
Da bei x = 2 der linksseitige Grenzwert der Ableitung von f nicht mit ihrem rechtsseitigen Grenzwert übereinstimmt, ist f dort nicht differenzierbar.
13.3
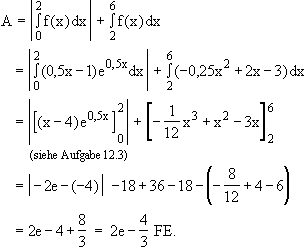
13.4
Nach 13.3 gilt: I =
=  = 4 – 2e ≈ –1,44;
= 4 – 2e ≈ –1,44;  =
=  =
=  ≈ 2,67
≈ 2,67
 Da I
Da I < 0, aber I
< 0, aber I + I
+ I > 0, muss ein
> 0, muss ein 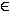 [2 ; 6] existieren, so dass
[2 ; 6] existieren, so dass
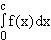 = 0 gilt.
= 0 gilt.
14.1
I. ae1930b = 2·109
II. ae2000b = 6·109
 70b = ln 3 ≈ 1,0986
70b = ln 3 ≈ 1,0986  b = 0,015694
b = 0,015694
b in I: ae30,29 = 2·109  1,4286·1013a = 2·109
1,4286·1013a = 2·109  a = 1,4·10–4
a = 1,4·10–4
14.2
0,00014e0,015694 · 1950 = 2,735·109
14.3
0,00014e0,015694 t = 1010  e0,015694 t = 7,143·1013
e0,015694 t = 7,143·1013
 0,015694 t = ln(7,143·1013) = 31,9
0,015694 t = ln(7,143·1013) = 31,9  t = 2032,6
t = 2032,6
Nach diesem Modell wird im Jahre 2032 die 10-Milliardengrenze überschritten.
14.4
0,00014e0,015694 t = 2  e0,015694 t = 14286
e0,015694 t = 14286
 0,015694 t = ln 14286 = 9,567
0,015694 t = ln 14286 = 9,567  t = 609,6
t = 609,6
Das Urelternpaar Adam und Eva hätte demnach am Anfang des
14.5
Der Verdoppelungszeitraum sei d. 
0,00014e0,015694 · (t + d) = 2 · 0,00014e0,015694 · t
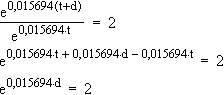
0,015694d = ln 2 = 0,69315  d = 44,167
d = 44,167
Demzufolge verdoppelt sich die Weltbevölkerung in 44 Jahren und 2 Monaten.
14.6
Das zu Grunde gelegte mathematische Wachstumsmodell hat mehrere gravierende Schwächen:
Erstens geht es von einer völlig gleichbleibenden „Wachstumsrate“ aus, schaltet also soziale Komponenten wie z.B. Geburtenkontrolle oder wirtschaftliche Komponenten (z.B. Babyboom in Zeiten der Prosperität) völlig aus.
Zweitens geht es von einer gleichbleibenden Lebenserwartung aus. Tatsächlich aber hat sich die Lebenserwartung in wenigen Jahrhunderten dank des hygienischen und medizinischen Fortschritts praktisch verdreifacht.
Drittens vernachlässigt es bevölkerungsrelevante Katastrofen wie Kriege oder verheerende Epidemien.
Daraus resultiert, dass die Menschheit in früheren Epochen sehr viel langsamer zunahm als in der Gegenwart, dass also der Parameter b in früheren Epochen viel kleiner war.
15.1
Aus dem Diagramm wird abgelesen:
f(0) = 25  aek·0 = a = 25
aek·0 = a = 25
f(15) = 5  25·ek·15 = 5
25·ek·15 = 5
 e15k = 0,2
e15k = 0,2  15k = ln 0,2
15k = ln 0,2  k ≈ –0,107
k ≈ –0,107
Probe:
f(8) = 25e–0,107·8 = 10,62 in ungefährer Übereinstimmung mit dem Diagrammwert.
15.2
Sei t0 irgendein Zeitpunkt und T der „Halbierungszeitraum“. Dann ist zum Zeitpunkt t0 + T nur noch die Hälfte derjenigen DDT-Belastung nachweisbar, die zum Zeitpunkt t0 gemessen wurde. Mathematisch ausgedrückt:
 2·f(t0 + T) = f(t0)
2·f(t0 + T) = f(t0)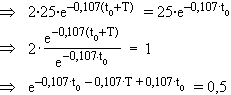
 e–0,107·T = 0,5
e–0,107·T = 0,5
 –0,107·T = ln 0,5 = –0,693
–0,107·T = ln 0,5 = –0,693
 T = 6,48
T = 6,48
Nach jeweils etwa 6,5 Jahren hat sich die DDT-Belastung halbiert.
16.1
Nach dem linken Grafen ist nach etwa 18 Tagen die gesamte Population durchseucht. Auch nach 40 Tagen hält die Epidemie unvermindert an.
Auch nach dem mittleren Grafen hat die Epidemie nach etwa 18 Tagen ihre maximale Ausbreitung erreicht und hält diesen Stand auch noch nach 40 Tagen. Sie betrifft aber nur etwas mehr als ein Drittel der Population.
Auch nach dem rechten Grafen betrifft die maximale Durchseuchung etwas mehr als ein Drittel der Population, ist aber schon nach 15 Tagen erreicht. Im Gegensatz zu den anderen Verläufen klingt sie aber bis zum 30. Tag wieder völlig ab.
16.2
Für große t gilt: e–0,5·t ≈ 0, d. h. n(t) ≈ 1500. Also kann nur der linke Graf zu n(t) gehören.
16.3
n(t)= 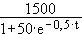

n'(t) = 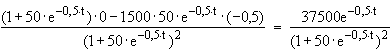
 n'(0) =
n'(0) =  = 14,42
= 14,42
Die Stelle der maximalen Ausbreitungsgeschwindigkeit ist gleich der Wendestelle von Gn mit maximaler Steigung von n. Also muss die Nullstelle von n'' bestimmt werden, an der n' ein Maximun annimmt.

Da n'' bei x = 7,82 sein Vorzeichen von + nach – wechselt, liegt dort ein Maximum von n' , also ein Maximun der Ausbreitungsgeschwindigkeit vor
16.4
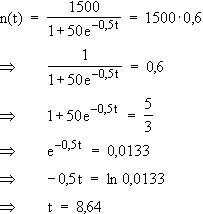
Nach 8,6 Tagen sind 60 % der Population infiziert.