f(x) = 2x ln x
ID = IR+, da ln x nur für x > 0 definiert ist.
= IR+, da ln x nur für x > 0 definiert ist.
Nullstellen von f: 2x ln x = 0  x = 0
x = 0  ln x = 0
ln x = 0
x = 0  ID
ID , also keine Nullstelle von f ;
, also keine Nullstelle von f ;
ln x = 0  x = 1
x = 1 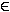 ID
ID , also Nullstelle von f.
, also Nullstelle von f.
f(x) = (x + 1) ln(–x)
ID = IR–, da ln (–x) nur für x < 0 definiert ist.
= IR–, da ln (–x) nur für x < 0 definiert ist.
Nullstellen von f: (x + 1) ln(–x) = 0  x + 1 = 0
x + 1 = 0  ln(–x) = 0
ln(–x) = 0
Beide Bedingungen ergeben x = –1 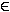 ID
ID
 x = –1 ist doppelte Nullstelle von f.
x = –1 ist doppelte Nullstelle von f.
f(x) = x ln(0,5x + 2)
Bestimmung von ID :
:
 ID
ID = ]-4; +∞[.
= ]-4; +∞[.
Nullstellen von f: x ln(0,5x + 2) = 0  x = 0
x = 0  ln(0,5x + 2) = 0
ln(0,5x + 2) = 0
x = 0 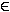 ID
ID , ist also Nullstelle von f ;
, ist also Nullstelle von f ;
 0,5x + 2 = 1
0,5x + 2 = 1  x = –2
x = –2 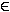 ID
ID
 x = –2 ist die zweite Nullstelle von f.
x = –2 ist die zweite Nullstelle von f.
f(x) = (x2 – 1) ln(x2 – 4)
Bestimmung von ID :
:
Die Parabel y = x2 – 4 hat die Nullstellen –2 und 2 und ist nach oben geöffnet
 ID
ID = ]-∞; -2[
= ]-∞; -2[  ]2; +∞[.
]2; +∞[.
Nullstellen von f: (x2 – 1) ln(x2 – 4) = 0  x2 – 1 = 0
x2 – 1 = 0  ln(x2 – 4) = 0
ln(x2 – 4) = 0
x2 – 1 = 0  x = ± 1
x = ± 1  ID
ID , also keine Nullstellen von f ;
, also keine Nullstellen von f ;
 – 4) = 0
– 4) = 0  x
x – 4 = 1
– 4 = 1  x =
x = 
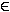 ID
ID
 x =
x =  sind die beiden Nullstellen von f.
sind die beiden Nullstellen von f.
f(x) = (x2 – 4) ln(x2 – 1)
Bestimmung von ID :
:
Die Parabel y = x2 – 1 hat die Nullstellen –1 und 1 und ist nach oben geöffnet
 ID
ID = ]-∞; –1[
= ]-∞; –1[  ]1; +∞[.
]1; +∞[.
Nullstellen von f: (x2 – 4) ln(x2 – 1) = 0  x2 – 4 = 0
x2 – 4 = 0  ln(x2 – 1) = 0
ln(x2 – 1) = 0
x2 – 4 = 0  x = ± 2
x = ± 2 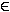 ID
ID , also Nullstellen von f ;
, also Nullstellen von f ;
 – 1) = 0
– 1) = 0  x
x – 1 = 1
– 1 = 1  x =
x = 
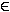 ID
ID ,
,
also ebenfalls Nullstellen von f.
f(x) = x2 ln(x2 + 1)
Bestimmung von ID :
:
ln(x2 + 1) ist genau dann definiert, wenn x2 + 1 > 0.
Da diese Bedingung immer erfüllt ist, gilt ID = IR.
= IR.
 x2 = 0
x2 = 0  ln(x2 + 1) = 0
ln(x2 + 1) = 0
x2 = 0  x = 0
x = 0 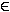 ID
ID , also doppelte Nullstelle von f ;
, also doppelte Nullstelle von f ;
ln(x2 + 1) = 0  x2 + 1 = 1
x2 + 1 = 1  x2 = 0
x2 = 0 
x = 0 ist wieder doppelte Nullstelle,
also insgesamt eine vierfache Nullstelle von f.
g)
f(x) = 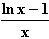
Bestimmung von ID :
:
ln x ist genau dann definiert, wenn x > 0.
Da dann der Nenner auch nicht null wird, gilt ID = IR+.
= IR+.
Nullstelle von f: 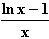 = 0
= 0  ln x – 1 = 0
ln x – 1 = 0  ln x = 1
ln x = 1
 x = e
x = e  ID
ID , also Nullstelle von f.
, also Nullstelle von f.
h)
f(x) = 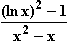
Bestimmung von ID :
:
ln x ist genau dann definiert, wenn x > 0.
 Der Nenner wird null, falls x = 0 oder x = 1
Der Nenner wird null, falls x = 0 oder x = 1
 ID
ID = IR+ \ {1}.
= IR+ \ {1}.
Nullstellen von f: 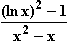 = 0
= 0  (ln x)
(ln x) – 1 = 0
– 1 = 0  (ln x)
(ln x) = 1
= 1  ln x = ± 1
ln x = ± 1
 x = e
x = e  x =
x =  .
.
Beide Werte liegen in ID , sind also Nullstellen von f.
, sind also Nullstellen von f.
i)
f(x) = 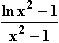
Bestimmung von ID :
:
ln x2 ist genau dann definiert, wenn x2 > 0, also wenn x ≠ 0.
 ID
ID = IR \ {–1; 0; 1}.
= IR \ {–1; 0; 1}.
Nullstellen von f: 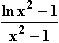 = 0
= 0  ln x
ln x – 1 = 0
– 1 = 0  ln x
ln x = 1
= 1
 x
x = e
= e  x =
x =  .
.
Beide Werte liegen in ID , sind also Nullstellen von f.
, sind also Nullstellen von f.
f(x) = 2x ln x; ID = IR+.
= IR+.
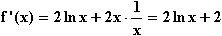
f '(x) = 0  2 ln x + 2 = 0
2 ln x + 2 = 0  ln x = –1
ln x = –1  x =
x = 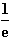 .
.
Da die Funktion y = ln x in IR+ monoton steigt, steigt auch f ' monoton und wechselt daher an ihrer Nullstelle das Vorzeichen von – nach +. Das bedeutet, dass der Graf von f für 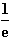
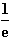
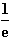

f(x) = (x + 1) ln(–x); ID = IR–.
= IR–.

f(x) = x ln(0,5x + 2); ID = ]-4; +∞[.
= ]-4; +∞[.
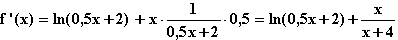
f(x) = (x2 – 1) ln(x2 – 4); ID = ]-∞; –2[
= ]-∞; –2[  ]2; +∞[.
]2; +∞[.
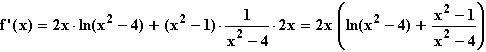
f(x) = (x2 – 4) ln(x2 – 1); ID = ]-∞; –1[
= ]-∞; –1[  ]1; +∞[.
]1; +∞[.
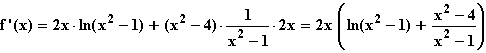
f(x) = x2 ln(x2 + 1); ID = IR.
= IR.
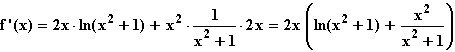
g)
f(x) = 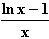 ; ID
; ID = IR
= IR .
.
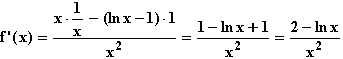
f '(x) = 0  2 – ln x = 0
2 – ln x = 0  ln x = 2
ln x = 2  x = e2.
x = e2.
Monotonieverhalten von f:
| 0 < x < | e2 | < x | |
|---|---|---|---|
| Zähler der Ableitungsfkt. | + | 0 | - |
| Nenner der Ableitungsfkt. | + | + | + |
| Steigung | + | 0 | - |
| Graph | steigt | HOP | fällt |
h)
f(x) = 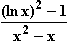 ; ID
; ID = IR
= IR \ {1}.
\ {1}.
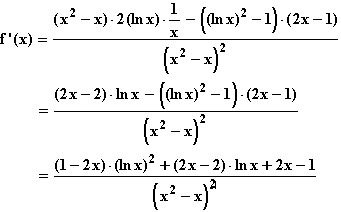
i)
f(x) = 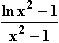 ; ID
; ID = IR \ {–1; 0; 1}.
= IR \ {–1; 0; 1}.
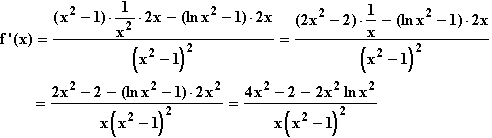
ln 0,5 + ln 2 = ln (0,5 · 2) = ln 1 = 0
b)
ln 8 – ln 4 = ln (8:4) = ln 2
c)
ln 25 + ln 5 = ln 52 + ln 5 = 2 ln 5 + ln 5 = 3 ln 5
d)
ln (10e2) = ln 10 + 2 ln e = 2 + ln 10
e)
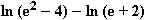 =
= 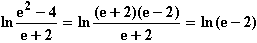
f)
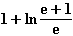 = 1 + ln (e + 1) – ln e = 1 + ln (e + 1) – 1 = ln (e + 1)
= 1 + ln (e + 1) – ln e = 1 + ln (e + 1) – 1 = ln (e + 1)
g)
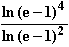 =
= 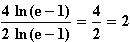
4.1 a)
f: x  ln (4 – 2x)
ln (4 – 2x)
(4 – 2x) > 0
> 0  4 – 2x ≠ 0
4 – 2x ≠ 0  x ≠ 2
x ≠ 2
 ID
ID = IR \ {2}.
= IR \ {2}.
b)
f: x  ln (2 – x)(1 + x)
ln (2 – x)(1 + x)
(2 – x)(1 + x) > 0

 –1 < x < 2
–1 < x < 2  ID
ID = ]-1; 2[.
= ]-1; 2[.
c)
f: x  ln
ln 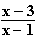
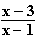 > 0
> 0  (x – 3)(x – 1) > 0
(x – 3)(x – 1) > 0

 x < 1
x < 1  x > 3
x > 3  ID
ID = ]-∞ 1[
= ]-∞ 1[  ]3; +∞[.
]3; +∞[.
4.2 a)
In ID = IR \ {2} gilt: f(x) = ln (4 – 2x)
= IR \ {2} gilt: f(x) = ln (4 – 2x) = 2 ln |4 – 2x| = 2 ln 2|2 – x|
= 2 ln |4 – 2x| = 2 ln 2|2 – x|
= 2 ( ln |x – 2| + ln 2 ) = 2 ln |x – 2| + 2 ln 2.
b)
In ID = ]-1; 2[ gilt: f(x) = ln (2 – x)(1 + x) = ln |2 – x| + ln |1 + x|
= ]-1; 2[ gilt: f(x) = ln (2 – x)(1 + x) = ln |2 – x| + ln |1 + x|
= ln (2 – x) + ln (x + 1).
c)
In ID = ]-∞; 1[
= ]-∞; 1[  ]3; +∞[ gilt: f(x) = ln
]3; +∞[ gilt: f(x) = ln 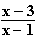 = ln |x – 3| – ln |x – 1|.
= ln |x – 3| – ln |x – 1|.
Das Weglassen der Betragsstriche würde hier dazu führen, dass der erste logarithmische Term nur für x > 3 und der zweite nur für x > 1 definiert wäre, so dass die ungeformte Funktion dann nur die Definitionsmenge ]3; +∞[ hätte.
f(x) = 2x ln x; ID = IR+.
= IR+.
0 < x  0
0  f(x)
f(x)  0, da nach de L'Hospital gilt:
0, da nach de L'Hospital gilt:
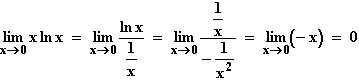
x  ∞
∞  f(x)
f(x)  ∞, da beide Faktoren 2x und ln x nach ∞ streben.
∞, da beide Faktoren 2x und ln x nach ∞ streben.
Der Graf von f besitzt demnach keine Asymptoten.
f(x) = (x + 1) ln(–x); ID = IR–.
= IR–.
0 > x  0
0  f(x)
f(x)  -∞, da x + 1
-∞, da x + 1  1 und ln(–x)
1 und ln(–x)  -∞.
-∞.
x  -∞
-∞  f(x)
f(x)  -∞, da x + 1
-∞, da x + 1  -∞ und ln(–x)
-∞ und ln(–x)  ∞.
∞.
Der Graf von f besitzt demnach die Asymptote x = 0.
f(x) = x ln(0,5x + 2); ID = ]-4; +∞[.
= ]-4; +∞[.
–4 < x  –4
–4  f(x)
f(x)  +∞, da der erste Faktor negativ ist und
+∞, da der erste Faktor negativ ist und
ln(0,5x + 2) nach
x  +∞
+∞  f(x)
f(x)  +∞, da beide Faktoren x und ln(0,5x + 2) nach +∞ streben.
+∞, da beide Faktoren x und ln(0,5x + 2) nach +∞ streben.
Der Graf von f besitzt demnach die Asymptote x = –4.
f(x) = (x2 – 1) ln(x2 – 4); ID = ]-∞; –2[
= ]-∞; –2[  ]2; +∞[.
]2; +∞[.
2 < x  2
2  f(x)
f(x)  -∞, da x2 – 1
-∞, da x2 – 1  3 und ln(x2 – 4)
3 und ln(x2 – 4)  -∞.
-∞.
x  +∞
+∞  f(x)
f(x)  +∞, da beide Faktoren nach +∞ streben.
+∞, da beide Faktoren nach +∞ streben.
Wegen der Achsensymmetrie des Grafen von f zur y-Achse gilt:
–2 > x  –2
–2  f(x)
f(x)  -∞ ;
-∞ ;
x  -∞
-∞  f(x)
f(x)  +∞ .
+∞ .
Der Graf von f besitzt demnach die Asymptoten x = –2 und x = 2.
f(x) = (x2 – 4) ln(x2 – 1); ID = ]-∞; –1[
= ]-∞; –1[  ]1; +∞[.
]1; +∞[.
1 < x  1
1  f(x)
f(x)  +∞, da x2 – 4
+∞, da x2 – 4  –3 und ln(x2 – 1)
–3 und ln(x2 – 1)  -∞.
-∞.
x  +∞
+∞  f(x)
f(x)  +∞, da beide Faktoren nach +∞ streben.
+∞, da beide Faktoren nach +∞ streben.
Wegen der Achsensymmetrie des Grafen von f zur y-Achse gilt:
–1 > x  –1
–1  f(x)
f(x)  +∞ ;
+∞ ;
x  -∞
-∞  f(x)
f(x)  +∞ .
+∞ .
Der Graf von f besitzt demnach die Asymptoten x = –1 und x = 1.
f(x) = x2 ln(x2 + 1); ID = IR.
= IR.
x  ±∞
±∞  f(x)
f(x)  +∞, da beide Faktoren nach +∞ streben.
+∞, da beide Faktoren nach +∞ streben.
Der Graf von f besitzt demnach keine Asymptoten.
g)
f(x) = 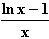 ; ID
; ID = IR
= IR .
.
0 < x  0
0  f(x)
f(x)  -∞, da der Zähler nach -∞ und der Nenner aus dem Positiven gegen 0 streben.
-∞, da der Zähler nach -∞ und der Nenner aus dem Positiven gegen 0 streben.
x  +∞
+∞  f(x)
f(x)  0, da nach de L'Hospital gilt:
0, da nach de L'Hospital gilt:
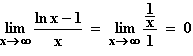
Der Graf von f besitzt demnach die Asymptoten x = 0 und y = 0.
h)
f(x) = 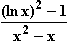 ; ID
; ID = IR
= IR \ {1}.
\ {1}.
0 < x  0
0  f(x)
f(x)  -∞, da wegen ln x
-∞, da wegen ln x  -∞ der Zähler nach +∞ strebt, während der Nenner x(x – 1) wegen x
-∞ der Zähler nach +∞ strebt, während der Nenner x(x – 1) wegen x  +0 und x – 1
+0 und x – 1  –1 aus dem Negativen gegen 0 strebt.
–1 aus dem Negativen gegen 0 strebt.
x  1
1  f(x)
f(x)  ± ∞, da wegen ln x
± ∞, da wegen ln x  0 der Zähler nach –1 strebt, während der Nenner bei x = 1 sein Vorzeichen von – nach + wechselt.
0 der Zähler nach –1 strebt, während der Nenner bei x = 1 sein Vorzeichen von – nach + wechselt.
x  +∞
+∞  f(x)
f(x)  0, da nach de L'Hospital gilt:
0, da nach de L'Hospital gilt:
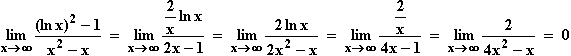
Der Graf von f besitzt demnach die Asymptoten x = 0, x = 1 und y = 0.
i)
f(x) = 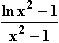 ; ID
; ID = IR \ {–1; 0; 1}.
= IR \ {–1; 0; 1}.
x  ±∞
±∞  f(x)
f(x)  0, da nach de L'Hospital gilt:
0, da nach de L'Hospital gilt:
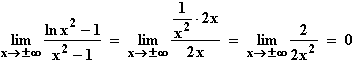
x  –1
–1  f(x)
f(x) 
 ∞, da wegen ln x
∞, da wegen ln x
 0 der Zähler nach –1 strebt, während der Nenner bei x = –1 sein Vorzeichen von + nach – wechselt.
0 der Zähler nach –1 strebt, während der Nenner bei x = –1 sein Vorzeichen von + nach – wechselt.
x  0
0  f(x)
f(x)  +∞, da der Zähler nach -∞ und der Nenner nach –1 streben.
+∞, da der Zähler nach -∞ und der Nenner nach –1 streben.
x  1
1  f(x)
f(x)  ± ∞, da wegen ln x
± ∞, da wegen ln x
 0 der Zähler nach –1 strebt, während der Nenner bei x = 1 sein Vorzeichen von – nach + wechselt.
0 der Zähler nach –1 strebt, während der Nenner bei x = 1 sein Vorzeichen von – nach + wechselt.
Der Graf von f besitzt demnach die Asymptoten
6. a)
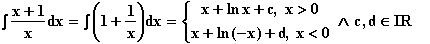
b)
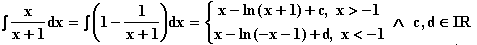
c)
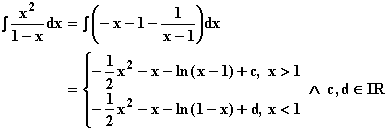
d)
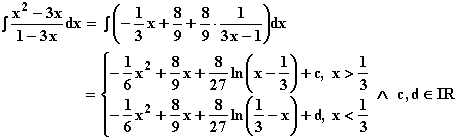
7.1
f(x) = 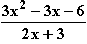
ID = IR \ {–1,5}
= IR \ {–1,5}
f(x) = 0  3x2 – 3x – 6 = 0
3x2 – 3x – 6 = 0  x1 = –1 ; x2 = 2
x1 = –1 ; x2 = 2
Da die Definitionslücke nicht im Intervall [-1; 2] liegt, ergibt sich der gesuchte Flächeninhalt A durch Integration von f in den Grenzen –1 und 2:
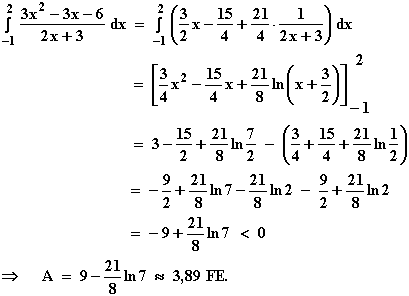
7.2
f(x) = 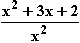
ID = IR \ {0}
= IR \ {0}
f(x) = 0  x2 + 3x + 2 = 0
x2 + 3x + 2 = 0  x1 = –2 ; x2 = –1
x1 = –2 ; x2 = –1
Da die Definitionslücke nicht im Intervall [-2; -1] liegt, ergibt sich der gesuchte Flächeninhalt A durch Integration von f in den Grenzen –2 und –1:
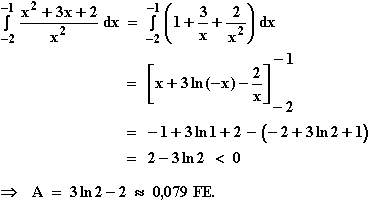
8.1
f(x) = x (ln x – 1)
Maximale Definitionsmenge: ID = IR+.
= IR+.
Verhalten für x  0: f(x)
0: f(x)  0 · (-∞): nicht bestimmbar, also de L'Hospital:
0 · (-∞): nicht bestimmbar, also de L'Hospital:
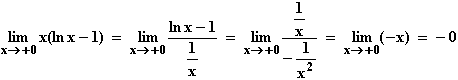
Verhalten für x  +∞: f(x)
+∞: f(x)  +∞, da beide Faktoren nach +∞ gehen.
+∞, da beide Faktoren nach +∞ gehen.
Nullstellen: f(x) = 0  x = 0
x = 0  ID
ID , also keine Nullstelle;
, also keine Nullstelle;
ln x – 1 = 0  ln x = 1
ln x = 1  x = e.
x = e.
Monotonie: f '(x) = 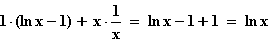
f '(x) = 0  ln x = 0
ln x = 0  x = 1
x = 1
Da f '(x) = ln x bei x = 1 das Vorzeichen von – nach + wechselt, fällt der Graf von f für
Krümmungsverhalten: f ''(x) = 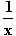 > 0 für x > 0
> 0 für x > 0  Der Graf von f ist im gesamten Definitionsbereich links gekrümmt.
Der Graf von f ist im gesamten Definitionsbereich links gekrümmt.
8.2
Graf von f:
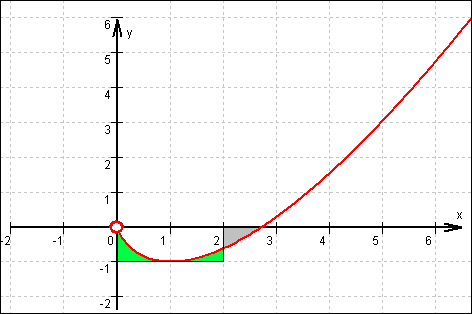
8.3
Die beiden grünen Flächenstücke, die zwischen x = 0 und x = 2 die Fläche zwischen dem Grafen von f und der x-Achse zu einem Rechteck mit dem Inhalt 2 FE ergänzen, sind zusammen nur geringfügig größer als die (abgeschnittene) graue Fläche. Das bedeutet, dass die Maßzahl der Fläche zwischen dem Grafen von f und der x-Achse sich nur wenig von 2 unterscheidet.
8.4
x·(ln x – 1) = x
x·(ln x – 1) – x = 0
x·(ln x – 1 – 1) = 0
x = 0  ID
ID , also keine Schnittstelle;
, also keine Schnittstelle;
ln x – 2 = 0  ln x = 2
ln x = 2  x = e2
x = e2
Der Schnittpunkt lautet also: S(e2|e2).
8.5
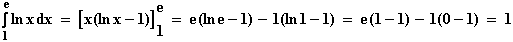
Die Maßzahl der Fläche beträgt 1.
9.1
f(x) = 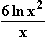
Maximale Definitionsmenge: x2 > 0  x ≠ 0, also: ID
x ≠ 0, also: ID = IR \ {0}.
= IR \ {0}.
Symmetrieverhalten: f(–x) =  = –f(x)
= –f(x) 
Der Graf von f ist punktsymmetrisch bzgl. des Ursprungs.
Verhalten für x  +0: f(x)
+0: f(x) 
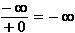
Verhalten für x  -0: f(x)
-0: f(x) 
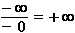
Verhalten für x  ± ∞ : f(x)
± ∞ : f(x) 
 : nicht bestimmbar, also de L'Hospital:
: nicht bestimmbar, also de L'Hospital:
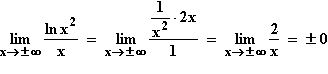
Aus dem Verhalten an den Definitionsrändern folgt, dass der Graf von f die folgenden Asymptoten besitzt:
Waagrechte Asymptote: y = 0; senkrechte Asymptote: x = 0.
Nullstellen: f(x) = 0  ln x2 = 0
ln x2 = 0  x2 = 1
x2 = 1  x = ± 1.
x = ± 1.
Extrempunkte: f '(x) = 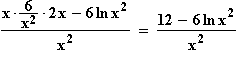
f '(x) = 0  12 – 6 ln x2 = 0
12 – 6 ln x2 = 0  ln x2 = 2
ln x2 = 2
 x2 = e2
x2 = e2  x = ± e
x = ± e
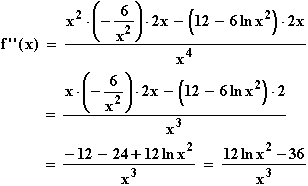
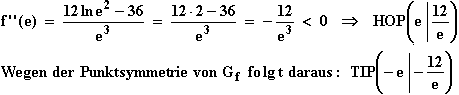
Wendepunkte: f ''(x) = 0  12 ln x2 – 36 = 0
12 ln x2 – 36 = 0  ln x2 = 3
ln x2 = 3
 einfache Nullstellen von f ''
einfache Nullstellen von f ''
 Wendestellen von f, also:
Wendestellen von f, also: 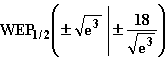
9.2
Graf von f und gesuchte Gerade von 9.3:
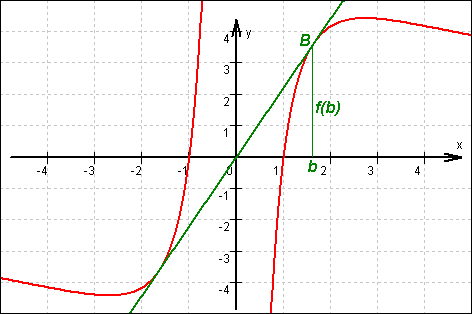
9.3
Die gesuchte Gerade aus der Schar y = mx berührt z. B. den rechten Ast des Grafen von f im Berührpunkt B(b|f(b)). Dann lässt sich die Steigung im Punkt B einmal als Ableitungswert von f an der Stelle b und zum andern als Kathetenverhältnis aus dem Steigungsdreieck der Tangente gewinnen:

Die Funktion g lautet dann: 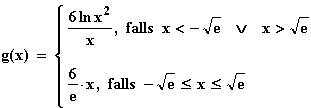
10.
f(x) = 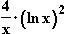
10.1
Maximale Definitionsmenge: x > 0 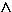 x ≠ 0
x ≠ 0  x > 0, also: ID
x > 0, also: ID = IR+.
= IR+.
10.2
Verhalten für x  +0: f(x)
+0: f(x)  (+∞) · (+∞) = +∞
(+∞) · (+∞) = +∞
Verhalten für x  +∞ : f(x)
+∞ : f(x)  0 · (+∞) : nicht bestimmbar, also de L'Hospital:
0 · (+∞) : nicht bestimmbar, also de L'Hospital:
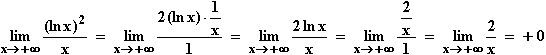
Aus dem Verhalten an den Definitionsrändern folgt, dass der Graf von f die folgenden Asymptoten besitzt:
Waagrechte Asymptote: y = 0; senkrechte Asymptote: x = 0.
10.3
Monotonie: 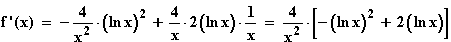
f '(x) = 0  –(ln x)2 + 2 ln x = 0
–(ln x)2 + 2 ln x = 0  –(ln x)·(ln x – 2) = 0
–(ln x)·(ln x – 2) = 0
 ln x = 0
ln x = 0  ln x = 2
ln x = 2  x = 1
x = 1  x = e2
x = e2
| 0 < x < | 1 | < x < | e2 | < x | |
|---|---|---|---|---|---|
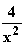 | + | + | + | + | + |
| –ln x | + | 0 | - | - | - |
| ln x – 2 | - | - | - | 0 | + |
| f '(x) | - | 0 | + | 0 | - |
G | fällt | TIP(1 | 0) | steigt | HOP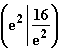 | fällt |
Krümmung:
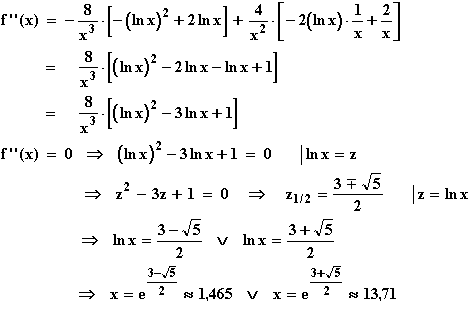
| 0 < x < | 1,465 | < x < | 13,71 | < x | |
|---|---|---|---|---|---|
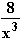 | + | + | + | + | + |
| (ln x)2 –3 ln x + 1 | + | 0 | - | 0 | + |
| f ''(x) | + | 0 | - | 0 | + |
| f '(x) | steigt | Steig.max. | fällt | Steig.min. | steigt |
G | links- gekrümmt | WEP (1,465 | 0,4) | rechts- gekrümmt | WEP (13,71 | 2) | links- gekrümmt |
10.4
Graf von f und zu berechnende Fläche von 10.7:
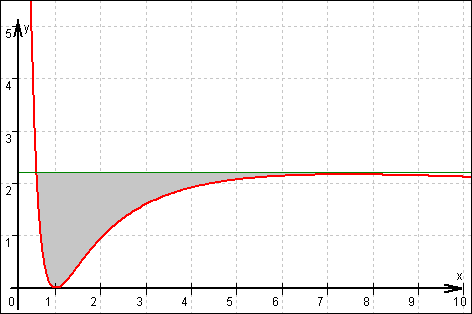
10.5
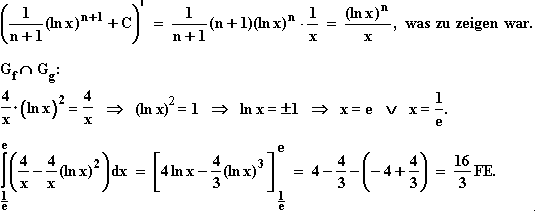
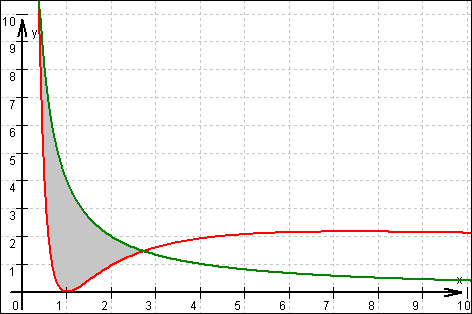
10.6
Die gesuchte Schnittstelle entspricht der linken Nullstelle der Funktion  .
.
Nach der Grafik von Aufgabe 10.4 muss diese Nullstelle etwa den Wert 0,5 haben.
Gewählt wird also ein Startwert links von 0,5, nämlich da, wo der Graf von d steiler verläuft, also z. B. z1 = 0,4.
Formel für das Newtonsche Näherungsverfahren: 

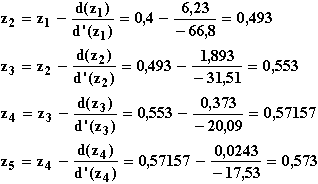
 Die gesuchte Schnittstelle lautet etwa x = 0,57.
Die gesuchte Schnittstelle lautet etwa x = 0,57.
10.7
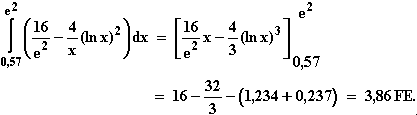
11.1
f(x) = 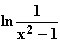
Maximale Definitionsmenge: x2 – 1 > 0  x < –1
x < –1  x > 1, also:
x > 1, also:
ID = IR \ [-1; 1] = ]-∞; -1[
= IR \ [-1; 1] = ]-∞; -1[  ]1; +∞[.
]1; +∞[.
Symmetrieverhalten: f(–x) = f(x) 
Der Graf von f ist achsensymmetrisch bzgl. der y-Achse.
Verhalten für 1 < x  1:
1: 
 +∞
+∞  f(x)
f(x)  +∞
+∞
Wegen der Achsensymmetrie gilt dann auch für –1 > x  –1: f(x)
–1: f(x)  +∞
+∞
Verhalten für x  ± ∞ :
± ∞ : 
 +0
+0  f(x)
f(x)  -∞
-∞
Aus dem Verhalten an den Definitionsrändern folgt:
Der Graf von f besitzt die senkrechten Asymptoten x = ±1.
Nullstellen: f(x) = 0 
 = 1
= 1  x
x – 1 = 1
– 1 = 1  x
x = 2
= 2  x = ±
x = ± 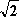 .
.
Monotonie: f '(x) = 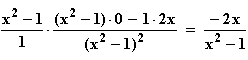
f '(x) = 0  x = 0
x = 0  ID
ID , also gibt es keine Horizontalstellen.
, also gibt es keine Horizontalstellen.
Da f '(x) für x < –1 positiv und für x > 1 negativ ist, folgt, dass f(x) für x < –1 monoton steigt und für x > 1 monoton fällt.
Krümmung: f ''(x) = 
Da die zweite Ableitung immer größer als Null ist, ist der Graf von f im ganzen Definitionsbereich von f linksgekrümmt.
11.2
Graf von f und gesuchte Parabel von 11.3:
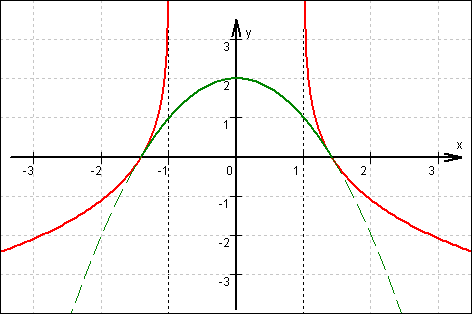
11.3
Die gesuchte quadratische Funktion g(x) = ax + b muss bei x =
+ b muss bei x = 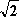 sowohl den selben Funktionswert als auch die selbe Steigung besitzen wie die Funktion f. Es ergeben sich also zwei Gleichungen mit den Unbekannten a und b:
sowohl den selben Funktionswert als auch die selbe Steigung besitzen wie die Funktion f. Es ergeben sich also zwei Gleichungen mit den Unbekannten a und b:
g(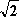 ) = f(
) = f(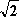 ) = 0
) = 0  a(
a(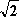 )
) + b = 0
+ b = 0  2a + b = 0
2a + b = 0
g '(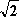 ) = f '(
) = f '(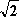 ) = –2
) = –2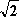
 2a
2a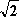 = –2
= –2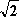
 a = –1
a = –1
a in die erste Gleichung eingesetzt ergibt dann b = 2.
12.1
f(x) = 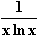
Maximale Definitionsmenge: x > 0 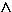 ln x ≠ 0
ln x ≠ 0  x > 0
x > 0 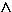 x ≠ 1, also:
x ≠ 1, also:
ID = IR+ \ {1}.
= IR+ \ {1}.
Verhalten für 0 < x  0: x ln x
0: x ln x  0 · (–∞) : nicht bestimmbar, also de L'Hospital:
0 · (–∞) : nicht bestimmbar, also de L'Hospital:
Verhalten für 1 > x  1: ln x
1: ln x  –0
–0  f(x)
f(x)  –∞
–∞
Verhalten für 1 < x  1: ln x
1: ln x  +0
+0  f(x)
f(x)  +∞
+∞
Verhalten für x  +∞ : x ln x
+∞ : x ln x  (+∞) · (+∞)
(+∞) · (+∞)  f(x)
f(x)  +0.
+0.
Aus dem Verhalten an den Definitionsrändern folgt, dass der Graf von f die folgenden Asymptoten besitzt:
Waagrechte Asymptote: y = 0; senkrechte Asymptoten: x = 0; x = 1.
Nullstellen: keine, da konstanter Zähler.
Monotonie:
f '(x) = 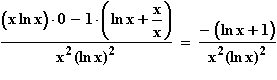
f '(x) = 0  ln x + 1 = 0
ln x + 1 = 0  ln x = –1
ln x = –1  x =
x =  .
.
| 0 < x < | 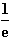 | < x < | 1 | < x | |
|---|---|---|---|---|---|
| –(ln x + 1) | + | 0 | - | - | - |
| x2(ln x)2 | + | + | + | 0 | + |
| f '(x) | + | 0 | - | # | - |
G | steigt | HOP( 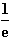 | –e) | –e) | fällt | # | fällt |
Krümmung:
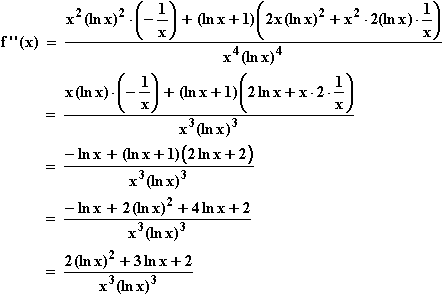
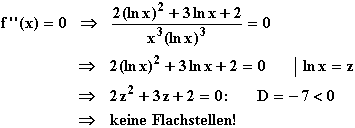
Da der z-Term eine nach oben geöffnete Parabel ohne Nullstellen darstellt, ist er und damit der Zähler von f '' immer größer als Null.
Der Nenner wechselt wegen (ln x)3 bei x=1 das Vorzeichen von – nach +. Da das folglich auch für den ganzen Term der zweiten Ableitung f '' gilt, ist der Graf von f für x < 1 rechts- und für x > 1 linksgekrümmt.
12.2
Graf von f :
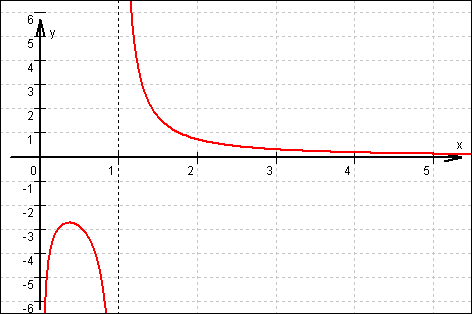
12.3
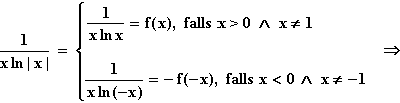
Ergänzt man den Grafen von f um sein Spiegelbild, das sich bei einer Punktspiegelung am Koordinatenursprung ergibt, so erhält man den Grafen von g.
12.4
Erforderliche Schritte:
- Aufstellung der Gleichung der Tangente an G
 in P(a | f(a)).
in P(a | f(a)). - Bestimmung der Tangenten-Nullstelle als Dreiecksgrundseite.
- Bestimmung des y-Achsenabschnitts der Tangente als Dreieckshöhe.
- Aufstellung der Formel für die Dreiecksfläche.
- Berechnung der zur Flächenmaßzahl 2,25 passenden Parameter a.
- Einsetzen der a-Werte in die Tangentengleichung von 1.
m = f '(a) sowie x = a und y = f(a) einesetzt:
f(a) = f '(a) · a + t
 t = f(a) – f '(a) · a
t = f(a) – f '(a) · a 
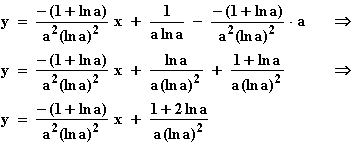
2. y = 0

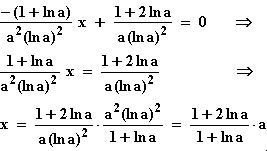
3. y-Achsenabschnitt:
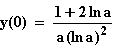
4. Dreiecksflächenformel:
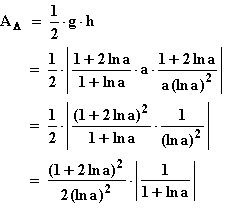
Laut Angabe soll gelten: a >
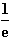
 ln a > –1
ln a > –1  Betragsstriche nicht nötig.
Betragsstriche nicht nötig.5. Berechnung von a:
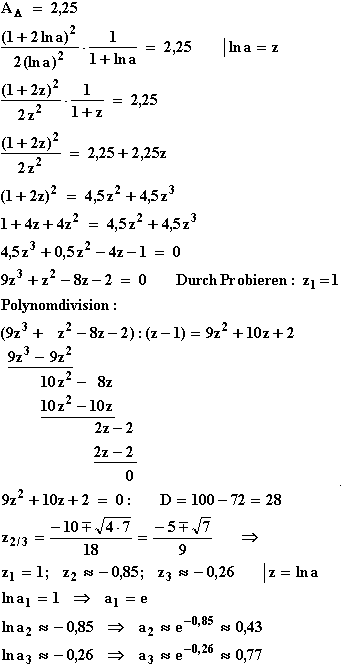
6. Einsetzen der a-Werte in die Tangentengleichung von 1.:

13.1
I. 4 = K + c ln 2  4 = K + 0,693 c
4 = K + 0,693 c
II. 6 = K + c ln 5  6 = K + 1,609 c
6 = K + 1,609 c
II. – I. 2 = 0,916 c  c = 2,183
c = 2,183  K = 2,487
K = 2,487
13.2
Es geht hier nicht um ein Maximum mit horizontaler Tangente, sondern darum, wann die echt monoton steigende Funktion E(R) den „kritischen“ Wert 10 erreicht:
E(R) = 10 = 2,487 + 2,183 ln(R)  2,183 ln(R) = 7,513
2,183 ln(R) = 7,513  ln(R) = 3,442
ln(R) = 3,442 
R = e3,442 = 31,25.
13.3
E(R) – E(0,5 R) = K + c ln(R) – ( K + c ln(0,5 R) )
= c ( ln(R) – ln(0,5 R) )
= c ln  = 2,183 ln 2 = 1,51
= 2,183 ln 2 = 1,51
E(10 R) – E(R) = K + c ln(10 R) – ( K + c ln(R) )
= c ( ln(10 R) – ln(R) )
= c ln  = 2,183 ln 10 = 5,03
= 2,183 ln 10 = 5,03
Eine Verzehnfachung des Reizes vergrößert also die Empfindung um ca. 5 Einheiten.
14.
Also: pH = –lg c(H3O+).
Der pH-Wert 1 bedeutet also: c(H3O+) = 10–1 mol/l.
a) Mit 9 Volumenteilen Wasser wird die Säure zehnfach verdünnt.
Damit gilt jetzt: c(H3O+) = 10–2 mol/l
 pH = 2 .
pH = 2 .b) Mit 4 Volumenteilen Wasser wird die Säure fünffach verdünnt.
Also gilt jetzt: c(H3O+) = 0,2 · 10–1 mol/l

pH = –lg (0,2 · 10–1) = –(lg 0,2 + lg 10–1) = –(–0,7 – 1) = 1,7 .
15.
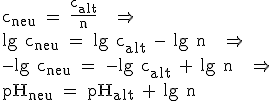
a) 3 = 1 + lg n
 lg n = 2
lg n = 2  n = 100
n = 100Zur hundertfachen Verdünnung der Säure muss 1 Volumenteil von ihr zu 99 Volumenteilen Wasser hinzugegeben werden.
b) 3,699 = 1 + lg n
 lg n = 2,699
lg n = 2,699  n = 500
n = 500Zur fünfhundertfachen Verdünnung der Säure muss 1 Volumenteil von ihr zu 499 Volumenteilen Wasser hinzugegeben werden.