Übungsblatt Rationale Funktionen
Lösungen zu Aufgabe 1
a) f
 (x) =
(x) = 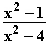 =
= 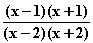
 Die Nullstellen sind x
Die Nullstellen sind x = 1 und x
= 1 und x = –1;
die Definitionslücken sind x
= –1;
die Definitionslücken sind x = 2 und x
= 2 und x = –2.
f
= –2.
f (x) =
(x) = 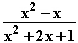 =
= 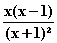
 Die Nullstellen sind x
Die Nullstellen sind x = 0 und x
= 0 und x = 1;
x
= 1;
x

 = –1 ist eine doppelte Definitionslücke.
f
= –1 ist eine doppelte Definitionslücke.
f (x) =
(x) = 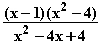 =
= 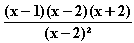 =
= 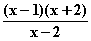
 Die Nullstellen sind x
Die Nullstellen sind x = 1 und x
= 1 und x = –2;
x
= –2;
x = 2 ist eine (einfache) Definitionslücke.
f
= 2 ist eine (einfache) Definitionslücke.
f (x) =
(x) = 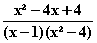 =
= 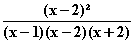
 Nullstellen sind keine vorhanden;
die Definitionslücken sind x
Nullstellen sind keine vorhanden;
die Definitionslücken sind x = 1, x
= 1, x = 2 und x
= 2 und x = –2.
b) Verhalten von f
= –2.
b) Verhalten von f an ihren Definitionslücken:
Da der Term von f
an ihren Definitionslücken:
Da der Term von f nicht kürzbar ist,
sind beide Definitionslücken Polstellen:
x
nicht kürzbar ist,
sind beide Definitionslücken Polstellen:
x 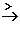 2
2  f
f (x) =
(x) = 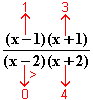
 +∞ .
Für x
+∞ .
Für x 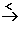 2 gilt dann wegen der Einfachheit
der Polstelle x = 2: f
2 gilt dann wegen der Einfachheit
der Polstelle x = 2: f (x)
(x)  –∞ .
x
–∞ .
x 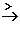 –2
–2  f
f (x) =
(x) = 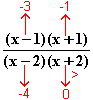
 –∞ .
Für x
–∞ .
Für x 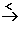 –2 gilt dann wegen der Einfachheit
der Polstelle x = –2: f
–2 gilt dann wegen der Einfachheit
der Polstelle x = –2: f (x)
(x)  +∞ .
Verhalten von f
+∞ .
Verhalten von f an ihrer Definitionslücke:
Da der Term von f
an ihrer Definitionslücke:
Da der Term von f nicht kürzbar ist,
ist die Definitionslücke x = –1 eine Polstelle:
x
nicht kürzbar ist,
ist die Definitionslücke x = –1 eine Polstelle:
x  –1
–1  f
f (x) =
(x) = 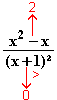
 +∞ .
(x = –1 ist doppelte Polstelle
+∞ .
(x = –1 ist doppelte Polstelle  gleiches Verhalten von f
gleiches Verhalten von f auf beiden Seiten der Polstelle)
Verhalten von f
auf beiden Seiten der Polstelle)
Verhalten von f an ihrer Definitionslücke:
Der Term von f
an ihrer Definitionslücke:
Der Term von f ist zwar kürzbar, behält aber
den Linearfaktor x – 2 im Nenner.
Also ist die Definitionslücke x = 2 eine Polstelle:
x
ist zwar kürzbar, behält aber
den Linearfaktor x – 2 im Nenner.
Also ist die Definitionslücke x = 2 eine Polstelle:
x 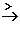 2
2  f
f (x) =
(x) = 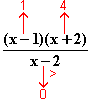
 +∞ .
Für x
+∞ .
Für x 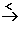 2 gilt dann wegen der Einfachheit
der Definitionslücke x = 2: f
2 gilt dann wegen der Einfachheit
der Definitionslücke x = 2: f (x)
(x)  –∞ .
Verhalten von f
–∞ .
Verhalten von f an ihren Definitionslücken:
f
an ihren Definitionslücken:
f (x) =
(x) = 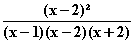

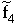 (x) =
(x) = 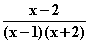 Da
Da 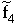 bei x = 2 im Gegensatz zu f
bei x = 2 im Gegensatz zu f definiert ist und dort
den Wert 0 hat, ist x = 2 eine hebbare Lücke von f
definiert ist und dort
den Wert 0 hat, ist x = 2 eine hebbare Lücke von f :
x
:
x  2
2  f
f (x)
(x) 
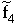 (2) = 0.
Die anderen Definitionslücken von f
(2) = 0.
Die anderen Definitionslücken von f sind Polstellen:
x
sind Polstellen:
x 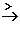 1
1 
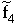 (x) =
(x) = 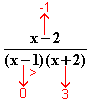
 –∞
–∞  f
f (x)
(x)  –∞ .
Für x
–∞ .
Für x 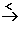 1 gilt dann wegen der Einfachheit
der Polstelle x = 1: f
1 gilt dann wegen der Einfachheit
der Polstelle x = 1: f (x)
(x)  +∞ .
x
+∞ .
x 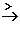 –2
–2 
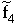 (x) =
(x) = 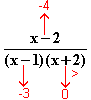
 +∞
+∞  f
f (x)
(x)  +∞ .
Für x
+∞ .
Für x 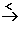 –2 gilt dann wegen der Einfachheit
der Polstelle x = –2: f
–2 gilt dann wegen der Einfachheit
der Polstelle x = –2: f (x)
(x)  –∞ .
–∞ .