Übungsblatt Rationale Funktionen
Lösungen zu Aufgabe 10
a) 1)
 fk und gk haben denselben Grad.
2) Ansatz für fk: fk(x) = ax³ + bx² + cx + d
fk und gk haben denselben Grad.
2) Ansatz für fk: fk(x) = ax³ + bx² + cx + d
 fk'(x) = 3ax² + 2bx + c; fk''(x) = 6ax + 2b
fk''(0) = 0
fk'(x) = 3ax² + 2bx + c; fk''(x) = 6ax + 2b
fk''(0) = 0  2b = 0
2b = 0  b = 0
fk'(0) = –3k²
b = 0
fk'(0) = –3k²  c = –3k²
fk(0) = y–Achsenabschnitt der Wendetangente = 2k³
c = –3k²
fk(0) = y–Achsenabschnitt der Wendetangente = 2k³
 d = 2k³
d = 2k³

 fk(x) = ax³ – 3k²x + 2k³
3) Ansatz für gk: gk(x) = Ax³ + Cx
fk(x) = ax³ – 3k²x + 2k³
3) Ansatz für gk: gk(x) = Ax³ + Cx  gk'(x) = 3Ax² + C
gk'(k) = –k³
gk'(x) = 3Ax² + C
gk'(k) = –k³  3Ak² + C = –k³
3Ak² + C = –k³  C = –3Ak² – k³
C = –3Ak² – k³

 gk(x) = Ax³ – (3Ak² + k³)x
4)
gk(x) = Ax³ – (3Ak² + k³)x
4)  x = –2k ist Nullstelle von fk und von gk
x = –2k ist Nullstelle von fk und von gk
 fk(–2k) = –8k³a + 6k³ + 2k³ = 0
fk(–2k) = –8k³a + 6k³ + 2k³ = 0  a = 1;
g
a = 1;
g (–2k) = –8k
(–2k) = –8k A + 6k
A + 6k A + 2k
A + 2k = 0
= 0  A = k
Demnach enthalten die Gleichungen von fk und gk nur
den Parameter k und lauten:
fk(x) = x³ – 3k²x + 2k³ ;
gk(x) = kx³ – 4k³x
A = k
Demnach enthalten die Gleichungen von fk und gk nur
den Parameter k und lauten:
fk(x) = x³ – 3k²x + 2k³ ;
gk(x) = kx³ – 4k³x
 h
h (x) =
(x) = 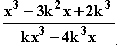 b) kx³ – 4k³x = 0
b) kx³ – 4k³x = 0  kx(x² – 4k²) = 0
kx(x² – 4k²) = 0  x1 = 0; x2/3 = ±2k
x1 = 0; x2/3 = ±2k
 IDmax = IR \ {0; ±2k}
Verhalten von hk bei den Definitionslücken:
1. x = –2k ist eine hebbare Lücke ( siehe a)! ).
Ermittlung des gekürzten Funktionsterms von hk:
IDmax = IR \ {0; ±2k}
Verhalten von hk bei den Definitionslücken:
1. x = –2k ist eine hebbare Lücke ( siehe a)! ).
Ermittlung des gekürzten Funktionsterms von hk:
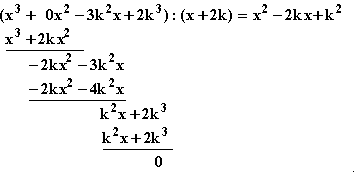

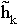 (x) =
(x) = 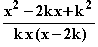 mit ID = IR \ {0; 2k}
mit ID = IR \ {0; 2k}
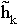 (–2k) =
(–2k) = 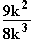 =
= 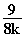 Also gilt für x
Also gilt für x  –2k: h
–2k: h (x)
(x) 
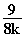 2. x = 2k ist eine (einfache) Polstelle.
x
2. x = 2k ist eine (einfache) Polstelle.
x 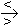 2k
2k  h
h (x) =
(x) = 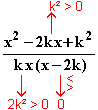

 ∞
3. x = 0 ist eine (einfache) Polstelle.
Für die Untersuchung des Verhalten von hk an dieser
Polstelle ist eine Fallunterscheidung nötig:
1. Fall: k > 0
x
∞
3. x = 0 ist eine (einfache) Polstelle.
Für die Untersuchung des Verhalten von hk an dieser
Polstelle ist eine Fallunterscheidung nötig:
1. Fall: k > 0
x 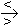 0
0  h
h (x) =
(x) = 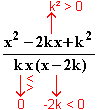
 ±∞
2. Fall: k < 0
x
±∞
2. Fall: k < 0
x 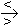 0
0  h
h (x) =
(x) = 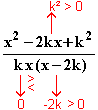
 ±∞
c) Nullstellen: x2 – 2kx + k2 = 0
±∞
c) Nullstellen: x2 – 2kx + k2 = 0  (x – k)2 = 0
(x – k)2 = 0  x1/2 = k
Asymptoten:
Es gibt zwei senkrechte Asymptoten mit den Gleichungen
x = 0 und x = 2k.
Durch Division der "Öffnungsfaktoren" des Zähler- und
Nennerpolynoms erhält man die Gleichung der waagrechten
Asymptote:
y =
x1/2 = k
Asymptoten:
Es gibt zwei senkrechte Asymptoten mit den Gleichungen
x = 0 und x = 2k.
Durch Division der "Öffnungsfaktoren" des Zähler- und
Nennerpolynoms erhält man die Gleichung der waagrechten
Asymptote:
y = 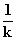 d) h
d) h '(x) =
'(x) = 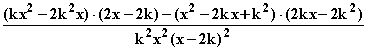 =
= 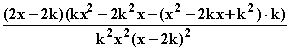 =
= 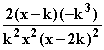 =
= 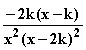 = 0
= 0  x = k
Monotonieverhalten von hk:
1. Fall: k > 0
x = k
Monotonieverhalten von hk:
1. Fall: k > 0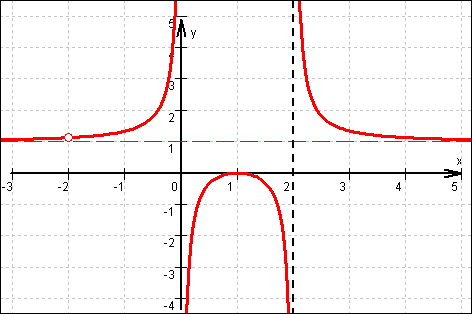 f) Der Graph von hk hat keine Wendepunkte.
Krümmungsverhalten von hk:
1. Fall: k > 0
f) Der Graph von hk hat keine Wendepunkte.
Krümmungsverhalten von hk:
1. Fall: k > 0