Übungsblatt Rationale Funktionen
Lösungen zu Aufgabe 2
a) f
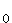 (x) =
(x) = 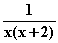
 Gleichungen der senkrechten Asymptoten: x = 0 und x = –2.
Wegen Zählergrad < Nennergrad lautet die
Gleichung der waagrechten Asymptote y = 0.
f
Gleichungen der senkrechten Asymptoten: x = 0 und x = –2.
Wegen Zählergrad < Nennergrad lautet die
Gleichung der waagrechten Asymptote y = 0.
f (x) =
(x) =  Wegen der negativen Nennerdiskriminante D = 2
Wegen der negativen Nennerdiskriminante D = 2 – 4·2 = –4 hat f
– 4·2 = –4 hat f keine Definitionslücken, also auch keine senkrechten Asymptoten.
Wegen Zählergrad < Nennergrad lautet die
Gleichung der waagrechten Asymptote y = 0.
f
keine Definitionslücken, also auch keine senkrechten Asymptoten.
Wegen Zählergrad < Nennergrad lautet die
Gleichung der waagrechten Asymptote y = 0.
f (x) =
(x) = 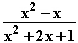 =
= 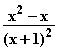
 Gleichung der senkrechten Asymptote: x = –1.
Wegen Zählergrad = Nennergrad existiert eine waagrechte Asymptote:
(1x² + ...) : (1x² + ...) = 1 + ...
Gleichung der senkrechten Asymptote: x = –1.
Wegen Zählergrad = Nennergrad existiert eine waagrechte Asymptote:
(1x² + ...) : (1x² + ...) = 1 + ...  Gleichung der waagrechten Asymptote y = 1.
f
Gleichung der waagrechten Asymptote y = 1.
f (x) =
(x) = 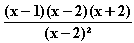 =
= 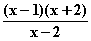 =
= 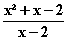
 Gleichung der senkrechten Asymptote: x = 2.
Wegen Zählergrad = Nennergrad + 1 existiert eine schiefe Asymptote:
(x² + x – 2) : (x – 2) = x + 3 +
Gleichung der senkrechten Asymptote: x = 2.
Wegen Zählergrad = Nennergrad + 1 existiert eine schiefe Asymptote:
(x² + x – 2) : (x – 2) = x + 3 + 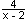 x² –2x
3x – 2
3x – 6
4
x² –2x
3x – 2
3x – 6
4
 Gleichung der schiefen Asymptote y = x + 3.
f
Gleichung der schiefen Asymptote y = x + 3.
f (x) =
(x) = 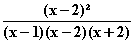

 (x) =
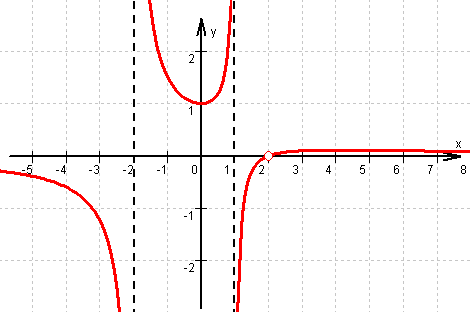
(x) = 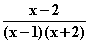 Gleichungen der senkrechten Asymptoten: x = 1 und x = –2.
Wegen Zählergrad < Nennergrad lautet die
Gleichung der waagrechten Asymptote y = 0.
b) Der Graph von f
Gleichungen der senkrechten Asymptoten: x = 1 und x = –2.
Wegen Zählergrad < Nennergrad lautet die
Gleichung der waagrechten Asymptote y = 0.
b) Der Graph von f verläuft genau dann oberhalb seiner Asymptote y = 0,
wenn f
verläuft genau dann oberhalb seiner Asymptote y = 0,
wenn f (x) > 0
(x) > 0  x² + 2x > 0
Nullstellen der Parabel: –2 und 0
x² + 2x > 0
Nullstellen der Parabel: –2 und 0
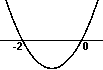
 x < –2 v x > 0
Also verläuft der Graph von f
x < –2 v x > 0
Also verläuft der Graph von f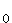 genau dann unterhalb seiner Asymptote
y = 0, wenn –2 < x < 0.
Der Graph von f
genau dann unterhalb seiner Asymptote
y = 0, wenn –2 < x < 0.
Der Graph von f verläuft genau dann oberhalb seiner Asymptote y = 0,
wenn f
verläuft genau dann oberhalb seiner Asymptote y = 0,
wenn f (x) > 0
(x) > 0  x > 0, da die Nennerparabel sowieso > 0 ist.
(Wegen D < 0 verläuft die Nennerparabel überall oberhalb der x-Achse!)
Also verläuft der Graph von f
x > 0, da die Nennerparabel sowieso > 0 ist.
(Wegen D < 0 verläuft die Nennerparabel überall oberhalb der x-Achse!)
Also verläuft der Graph von f genau dann unterhalb seiner Asymptote
y = 0, wenn x < 0.
Zerlegung des Terms von f
genau dann unterhalb seiner Asymptote
y = 0, wenn x < 0.
Zerlegung des Terms von f durch Polynomdivision:
(x² – x + 0) : (x² + 2x + 1) = 1 –
durch Polynomdivision:
(x² – x + 0) : (x² + 2x + 1) = 1 – 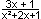 x² +2x + 1
–3x – 1
Also verläuft der Graph von f
x² +2x + 1
–3x – 1
Also verläuft der Graph von f genau dann oberhalb seiner Asymptote
y = 1, wenn
genau dann oberhalb seiner Asymptote
y = 1, wenn 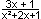 < 0 | · (x²+2x+1): in ID immer > 0 !
3x + 1 < 0
< 0 | · (x²+2x+1): in ID immer > 0 !
3x + 1 < 0  x < –
x < –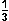 Also verläuft der Graph von f
Also verläuft der Graph von f genau dann unterhalb seiner Asymptote
y = 1, wenn x > –
genau dann unterhalb seiner Asymptote
y = 1, wenn x > –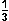 .
Nach a) gilt: f
.
Nach a) gilt: f (x) = x + 3 +
(x) = x + 3 + 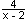 Also verläuft der Graph von f
Also verläuft der Graph von f genau dann oberhalb seiner Asymptote
y = x + 3, wenn
genau dann oberhalb seiner Asymptote
y = x + 3, wenn 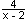 > 0
> 0  x – 2 > 0
x – 2 > 0  x > 2
Also verläuft der Graph von f
x > 2
Also verläuft der Graph von f genau dann unterhalb seiner Asymptote
y = x + 3, wenn x < 2
Der Graph von f
genau dann unterhalb seiner Asymptote
y = x + 3, wenn x < 2
Der Graph von f verläuft genau dann oberhalb / unterhalb seiner
Asymptote y = 0, wenn f
verläuft genau dann oberhalb / unterhalb seiner
Asymptote y = 0, wenn f (x) > / < 0, also
(x) > / < 0, also 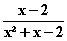 > / < 0
Nullstelle der Zählergeraden: 2
Nullstellen der Nennerparabel: –2 und 1
> / < 0
Nullstelle der Zählergeraden: 2
Nullstellen der Nennerparabel: –2 und 1 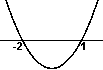
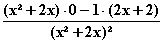 =
= 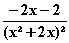 f
f –2x – 2 = 0
–2x – 2 = 0 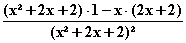 =
= 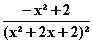 f
f
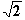 Monotonieverhalten von f
Monotonieverhalten von f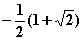 )
)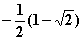 )
)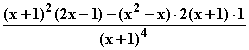 =
= 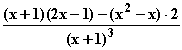 =
= 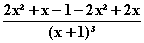 =
= 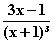 f
f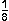 )
)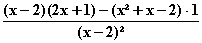 =
= 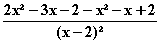 =
= 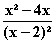 f
f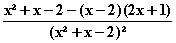 =
= 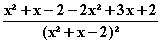 =
= 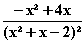 f
f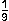 )
)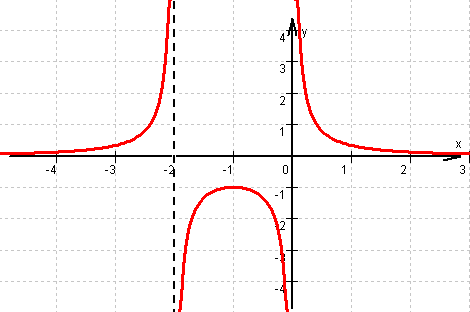 Graph von f
Graph von f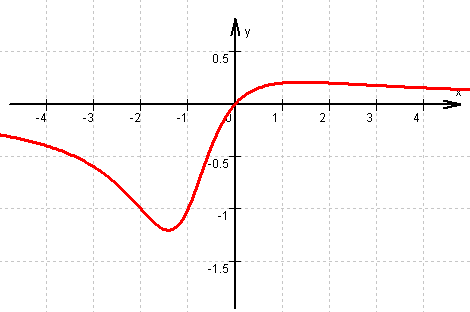 Graph von f
Graph von f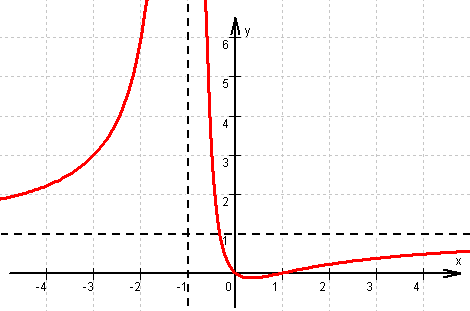 Graph von f
Graph von f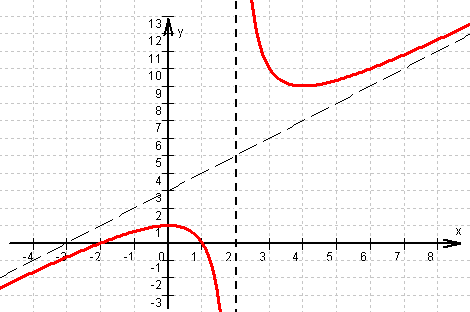 Graph von f
Graph von f