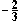Übungsblatt Rationale Funktionen
Lösungen zu Aufgabe 3
a) Symmetrieverhalten: f(–x) =
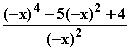 =
= 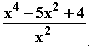 = f(x)
= f(x)  G
G ist achsensymmetrisch bzgl. der y–Achse.
Nullstellen:
f(x) = 0
ist achsensymmetrisch bzgl. der y–Achse.
Nullstellen:
f(x) = 0  x
x – 5x
– 5x + 4 = 0; Setze x
+ 4 = 0; Setze x = z
= z  z
z – 5z + 4 = 0; D = 5² – 4·1·4 = 9
– 5z + 4 = 0; D = 5² – 4·1·4 = 9  z
z

 =
= 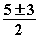
 z
z = 4; z
= 4; z = 1. Setze z = x
= 1. Setze z = x
 x
x = 4
= 4  x
x = 1
= 1  x
x

 = ±2; x
= ±2; x

 = ±1
Verhalten an der Definitionslücke:
x
= ±1
Verhalten an der Definitionslücke:
x  0
0  f(x) =
f(x) = 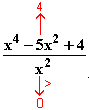
 +∞
b) Kürzen von f(x): f(x) = x
+∞
b) Kürzen von f(x): f(x) = x – 5 +
– 5 + 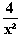
 Gleichung der asymptotischen Kurve: a(x) = x
Gleichung der asymptotischen Kurve: a(x) = x – 5;
x
– 5;
x  ±∞
±∞  f(x)
f(x)  +∞, da a(x)
+∞, da a(x)  +∞
c) f '(x) =
+∞
c) f '(x) = 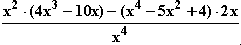 =
= 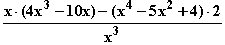 =
= 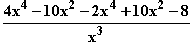 =
= 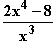 = 0
= 0  2x
2x – 8 = 0
– 8 = 0  x
x = 4
= 4  x
x = 2
= 2  x
x

 = ±
= ±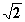 Monotonieverhalten von f:
Monotonieverhalten von f: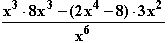 =
= 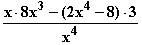 =
= 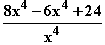 =
= 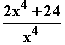 f ''(x) = 0: keine Lösung, da der Zähler von f '' nicht 0 werden kann.
Also hat Gf keine Wendepunkte.
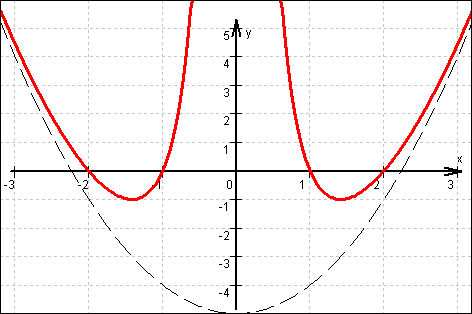
d) Graph von f:
f ''(x) = 0: keine Lösung, da der Zähler von f '' nicht 0 werden kann.
Also hat Gf keine Wendepunkte.
d) Graph von f:
 e)
e) 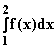 =
= 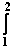 (x² – 5 +
(x² – 5 + 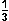 x³ – 5x –
x³ – 5x – 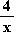
 =
=