Übungsblatt Rationale Funktionen
Lösungen zu Aufgabe 4
a) Symmetrieverhalten: f(–x) =
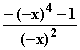 =
= 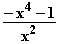 = f(x)
= f(x)  G
G ist achsensymmetrisch bzgl. der y–Achse.
Verhalten an der Definitionslücke:
x
ist achsensymmetrisch bzgl. der y–Achse.
Verhalten an der Definitionslücke:
x  0
0  f(x) =
f(x) = 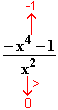
 –∞
Nachweis der Nullstellenfreiheit:
f(x) = 0
–∞
Nachweis der Nullstellenfreiheit:
f(x) = 0  –x
–x – 1 = 0
– 1 = 0  x
x = –1
Da x
= –1
Da x ≥ 0 für alle x
≥ 0 für alle x 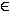 IR, hat die Gleichung keine Lösung.
Verlauf des Graphen:
f(x) =
IR, hat die Gleichung keine Lösung.
Verlauf des Graphen:
f(x) = 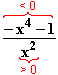 < 0 für alle x
< 0 für alle x 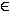 IR\{0},
d. h. Gf verläuft nur im 3. und 4. Quadranten.
b) Kürzen von f(x): f(x) = –x
IR\{0},
d. h. Gf verläuft nur im 3. und 4. Quadranten.
b) Kürzen von f(x): f(x) = –x –
– 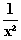
 Gleichung der asymptotischen Kurve: a(x) = –x
Gleichung der asymptotischen Kurve: a(x) = –x ;
x
;
x  ±∞
±∞  f(x)
f(x)  –∞, da a(x)
–∞, da a(x)  –∞
c) f '(x) =
–∞
c) f '(x) = 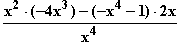 =
= 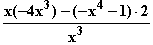 =
= 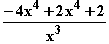 =
= 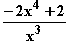 = 0
= 0  –2x
–2x + 2 = 0
+ 2 = 0  x
x = 1
= 1  x
x

 = ±1
Monotonieverhalten von f:
= ±1
Monotonieverhalten von f: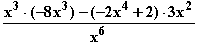 =
= 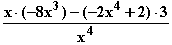 =
= 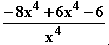 =
= 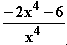 f ''(x) = 0: keine Lösung, da der Zähler von f '' nicht 0 werden kann.
Also hat Gf keine Wendepunkte.
d) Graph von f:
f ''(x) = 0: keine Lösung, da der Zähler von f '' nicht 0 werden kann.
Also hat Gf keine Wendepunkte.
d) Graph von f:
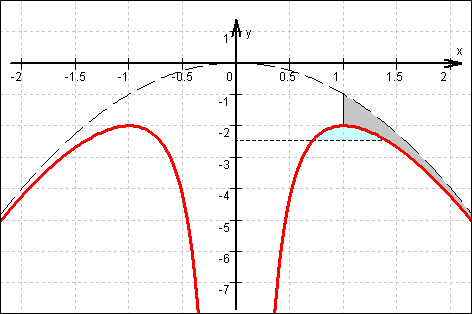 e) Menge aller Stammfunktionen von f :
F
e) Menge aller Stammfunktionen von f :
F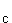 (x) =
(x) = 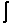
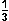 x
x +
+ 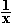 + c, c
+ c, c 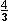 f) Bestimmung der Abszissen der Schnittpunkte von Gf
und der Geraden g: y = –2,5 im 4. Quadranten:
f) Bestimmung der Abszissen der Schnittpunkte von Gf
und der Geraden g: y = –2,5 im 4. Quadranten:
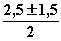 , also z
, also z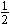 Setze z = x
Setze z = x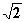 , x
, x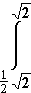 (
(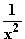 + 2,5) dx
= –
+ 2,5) dx
= –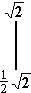 =
= 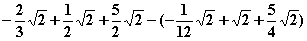 =
= 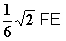 g) Sei c > 1. Zunächst berechnet man die Fläche A(c) zwischen Gf,
der Parabel y = –x
g) Sei c > 1. Zunächst berechnet man die Fläche A(c) zwischen Gf,
der Parabel y = –x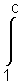 (–x
(–x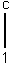 = –
= –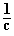 + 1
+ 1