Übungsblatt Rationale Funktionen
Lösungen zu Aufgabe 5
a) Symmetrieverhalten:
f(–x) = 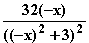 =
= 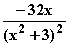 = –f(x)
= –f(x)  G
G ist punktsymmetrisch bzgl. des Koordinatenursprungs.
Verhalten für x
ist punktsymmetrisch bzgl. des Koordinatenursprungs.
Verhalten für x  ±∞:
f(x)
±∞:
f(x)  0, da Zählergrad von f < Nennergrad von f.
Verlauf des Graphen:
x
0, da Zählergrad von f < Nennergrad von f.
Verlauf des Graphen:
x 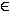 IR
IR
 f(x) =
f(x) = 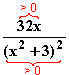 > 0
> 0
 Gf verläuft für x > 0 nur im 1. Quadranten.
Wegen der Punktsymmetrie bzgl. O verläuft Gf für x < 0
nur im 3. Quadranten.
Grobskizze:
Gf verläuft für x > 0 nur im 1. Quadranten.
Wegen der Punktsymmetrie bzgl. O verläuft Gf für x < 0
nur im 3. Quadranten.
Grobskizze:
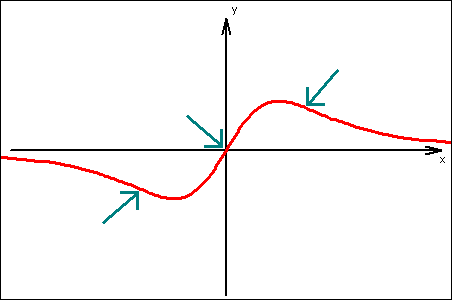 Anzahl der Wendepunkte: 3 (
Anzahl der Wendepunkte: 3 ( Pfeile in der Grobskizze)
b) f '(x) =
Pfeile in der Grobskizze)
b) f '(x) = 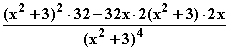 =
= 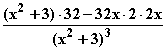 =
= 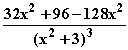 =
= 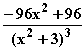 = 0
= 0  –96x
–96x + 96 = 0
+ 96 = 0  x
x = 1
= 1  x
x

 = ±1
Monotonieverhalten von f:
= ±1
Monotonieverhalten von f:
| | x < | –1 | < x < | 1 | < x |
|---|
| Zähler der Ableitungsfkt. | – | 0 | + | 0 | – |
| Nenner der Ableitungsfkt. | + | + | + | + | + |
| Steigung | – | 0 | + | 0 | – |
| Graph | fällt | TIP
(–1|–2) | steigt | HOP
(1|2) | fällt |
f ''(x) = 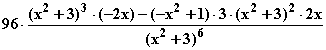 =
= 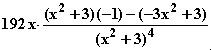 =
= 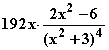 = 0
= 0  x
x = 0, x
= 0, x

 = ±
= ±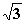 Da es sich um drei einfache Nullstellen von f '' handelt,
sind sie Wendestellen von Gf.
Koordinaten der Wendepunkte:
WEP
Da es sich um drei einfache Nullstellen von f '' handelt,
sind sie Wendestellen von Gf.
Koordinaten der Wendepunkte:
WEP (0|0), WEP
(0|0), WEP (
(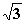 |
|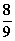
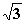 ), WEP
), WEP (–
(–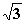 |–
|–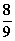
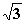 )
c) Ansatz für die Wendetangente bei x = 0: y = m·x;
m = f '(0) =
)
c) Ansatz für die Wendetangente bei x = 0: y = m·x;
m = f '(0) = 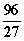 =
= 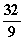 Die Gleichung der Wendetangente bei x = 0 lautet also y =
Die Gleichung der Wendetangente bei x = 0 lautet also y = 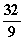 x
Ansatz für die Wendetangente bei x =
x
Ansatz für die Wendetangente bei x =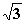 : y = m·x + t;
m = f '(
: y = m·x + t;
m = f '(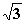 ) =
) = 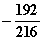 =
= 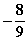 m und WEP
m und WEP in den Tangentenansatz einsetzen:
in den Tangentenansatz einsetzen:
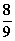
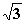 =
= 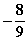 ·
·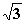 + t
+ t  t =
t = 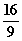
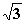 Die Gleichung der Wendetangente bei x =
Die Gleichung der Wendetangente bei x =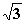 lautet also:
y =
lautet also:
y = 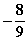 x +
x + 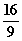
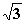 Wegen der Punktsymmetrie von Gf bzgl. O lautet dann die
Gleichung der Wendetangente bei x = –
Wegen der Punktsymmetrie von Gf bzgl. O lautet dann die
Gleichung der Wendetangente bei x = –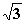 :
y = –(
:
y = –(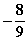 (–x) +
(–x) + 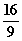
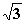 ) =
) = 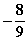 x –
x – 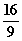
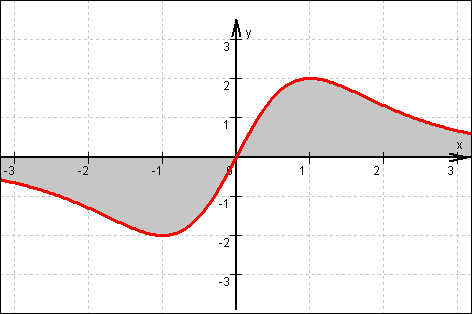
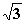 d) Graph von f:
d) Graph von f:
 e) F '(x) =
e) F '(x) = 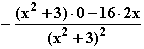 =
= 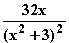 = f(x)
= f(x)  F ist eine Stammfunktion von f.
f) Wegen der Punktsymmetrie von Gf ist die gesuchte Fläche gleich der
doppelten Fläche zwischen Gf und der x–Achse im 1. Quadranten.
Um diese zu berechnen, wird sie zunächst bei x = c, c > 0
abgeschnitten, und dann der Grenzprozess c
F ist eine Stammfunktion von f.
f) Wegen der Punktsymmetrie von Gf ist die gesuchte Fläche gleich der
doppelten Fläche zwischen Gf und der x–Achse im 1. Quadranten.
Um diese zu berechnen, wird sie zunächst bei x = c, c > 0
abgeschnitten, und dann der Grenzprozess c  ∞ betrachtet:
A(c) =
∞ betrachtet:
A(c) = 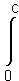
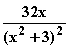 dx =
dx = 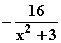
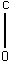 =
= 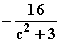 – (–
– (–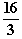 )
) 
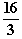 für c
für c  ∞
∞  Gesuchte Fläche A = 2·
Gesuchte Fläche A = 2·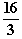 =
= 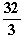 FE.
FE.
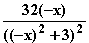 =
= 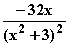 = –f(x)
= –f(x)  G
G ist punktsymmetrisch bzgl. des Koordinatenursprungs.
Verhalten für x
ist punktsymmetrisch bzgl. des Koordinatenursprungs.
Verhalten für x  ±∞:
f(x)
±∞:
f(x)  0, da Zählergrad von f < Nennergrad von f.
Verlauf des Graphen:
x
0, da Zählergrad von f < Nennergrad von f.
Verlauf des Graphen:
x 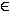 IR
IR
 f(x) =
f(x) = 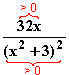 > 0
> 0
 Gf verläuft für x > 0 nur im 1. Quadranten.
Wegen der Punktsymmetrie bzgl. O verläuft Gf für x < 0
nur im 3. Quadranten.
Grobskizze:
Gf verläuft für x > 0 nur im 1. Quadranten.
Wegen der Punktsymmetrie bzgl. O verläuft Gf für x < 0
nur im 3. Quadranten.
Grobskizze:
 Anzahl der Wendepunkte: 3 (
Anzahl der Wendepunkte: 3 ( Pfeile in der Grobskizze)
b) f '(x) =
Pfeile in der Grobskizze)
b) f '(x) = 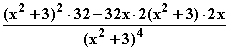 =
= 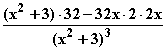 =
= 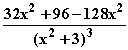 =
= 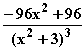 = 0
= 0  –96x
–96x + 96 = 0
+ 96 = 0  x
x = 1
= 1  x
x

 = ±1
Monotonieverhalten von f:
= ±1
Monotonieverhalten von f: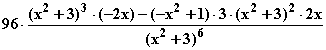 =
= 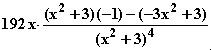 =
= 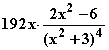 = 0
= 0  = ±
= ±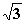 Da es sich um drei einfache Nullstellen von f '' handelt,
sind sie Wendestellen von Gf.
Koordinaten der Wendepunkte:
WEP
Da es sich um drei einfache Nullstellen von f '' handelt,
sind sie Wendestellen von Gf.
Koordinaten der Wendepunkte:
WEP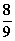
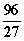 =
= 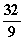 Die Gleichung der Wendetangente bei x = 0 lautet also y =
Die Gleichung der Wendetangente bei x = 0 lautet also y = 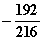 =
= 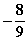 m und WEP
m und WEP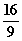
 e) F '(x) =
e) F '(x) = 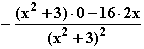 =
= 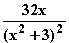 = f(x)
= f(x) 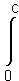
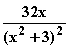 dx =
dx = 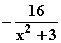
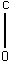 =
= 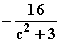 – (–
– (–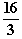 )
) 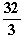 FE.
FE.