Übungsblatt Rationale Funktionen
Lösungen zu Aufgabe 6
a) Nullstellen: f(x) = 0
 2x – x
2x – x = 0
= 0  x(2 – x) = 0
x(2 – x) = 0  x
x = 0; x
= 0; x = 2
Da x
= 2
Da x und x
und x in der Definitionsmenge von f enthalten sind,
sind sie Nullstellen von f.
Asymptoten des Graphen:
Gleichung der senkrechten Asymptote: x = 1
Wegen der Gleichheit des Zähler- und des Nennergrads gibt es
auch eine waagrechte Asymptote:
in der Definitionsmenge von f enthalten sind,
sind sie Nullstellen von f.
Asymptoten des Graphen:
Gleichung der senkrechten Asymptote: x = 1
Wegen der Gleichheit des Zähler- und des Nennergrads gibt es
auch eine waagrechte Asymptote:
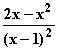 = (–x
= (–x + 2x) : (x
+ 2x) : (x – 2x + 1) = –1 + echt-gebrochen-rat. Fkt.
– 2x + 1) = –1 + echt-gebrochen-rat. Fkt.
 Gleichung der waagrechten Asymptote: y = –1
b) f '(x) =
Gleichung der waagrechten Asymptote: y = –1
b) f '(x) = 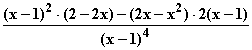 =
= 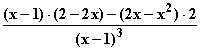 =
= 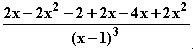 =
= 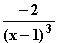 ≠ 0 für alle x
≠ 0 für alle x 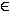 IR.
Monotonieverhalten von f:
IR.
Monotonieverhalten von f: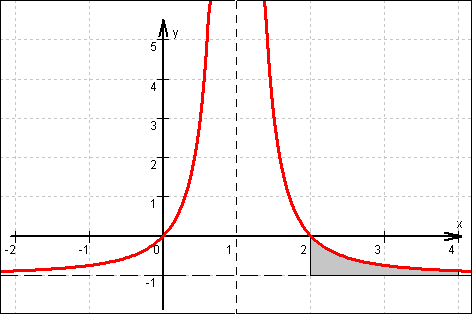 d) F '(x) =
d) F '(x) = 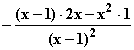 =
= 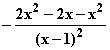 =
= 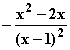 = f(x)
= f(x) 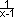 –x² + x
–x + 0
–x + 1
–1
–x² + x
–x + 0
–x + 1
–1
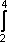 (f(x) – (–1))dx =
(f(x) – (–1))dx = 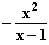 + x
+ x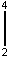 =
= 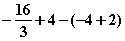 =
= 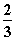 FE.
FE.