Übungsblatt Rationale Funktionen
Lösungen zu Aufgabe 7
a) f(x) = x
 – 3x – 2
x
– 3x – 2
x  ±∞
±∞  f(x)
f(x)  ±∞
Nullstellen:
x
±∞
Nullstellen:
x = –1; Polynomdivision:
= –1; Polynomdivision:
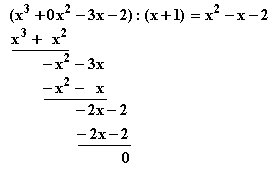
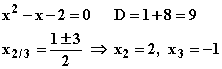 Horizontalpunkte:
f '(x) = 3x
Horizontalpunkte:
f '(x) = 3x – 3 = 0
– 3 = 0  x
x = 1
= 1  x
x

 = ±1
Wegen des Verhaltens von f für x
= ±1
Wegen des Verhaltens von f für x  ±∞ liegt bei
x = –1 ein HOP und bei x = 1 ein TIP vor:
HOP(–1|0); TIP(1|–4)
Wendepunkt: Mitte zwischen HOP und TIP, also WEP(0|–2)
g(x) =
±∞ liegt bei
x = –1 ein HOP und bei x = 1 ein TIP vor:
HOP(–1|0); TIP(1|–4)
Wendepunkt: Mitte zwischen HOP und TIP, also WEP(0|–2)
g(x) = 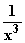 (x
(x – 3x – 2) =
– 3x – 2) = 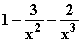
 Waagrechte Asymptote mit der Gleichung y = 1.
Polstelle x = 0 mit Vorzeichenwechsel von g
Waagrechte Asymptote mit der Gleichung y = 1.
Polstelle x = 0 mit Vorzeichenwechsel von g  Senkrechte Asymptote mit der Gleichung x = 0.
Nullstellen: die selben wie von f, also x
Senkrechte Asymptote mit der Gleichung x = 0.
Nullstellen: die selben wie von f, also x

 = –1; x
= –1; x = 2
Monotonieverhalten:
g'(x) =
= 2
Monotonieverhalten:
g'(x) = 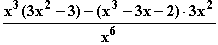 =
= 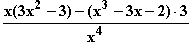 =
= 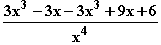 =
= 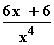 g'(x) = 0
g'(x) = 0  6x + 6 = 0
6x + 6 = 0  x = –1
x = –1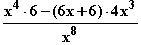 =
= 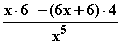 =
= 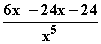 =
= 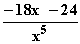 = 0
= 0 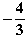 einfache Nullstelle von g''
einfache Nullstelle von g'' 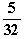 ).
Graphen von f, g und h:
).
Graphen von f, g und h:
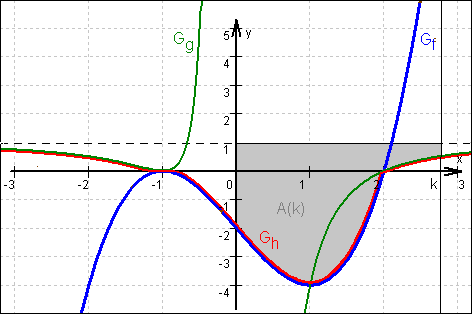 b) f(–1) = g(–1) = 0
b) f(–1) = g(–1) = 0 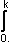 (1 – h(x))dx =
(1 – h(x))dx = 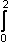 (1 – f(x))dx +
(1 – f(x))dx + 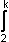 (1 – g(x))dx
=
(1 – g(x))dx
= 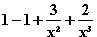 )dx
=
)dx
= 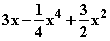
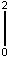
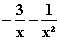
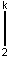 =
= 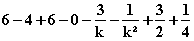 =
= 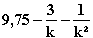 FE.
k
FE.
k