Übungsblatt Rationale Funktionen
Lösungen zu Aufgabe 8
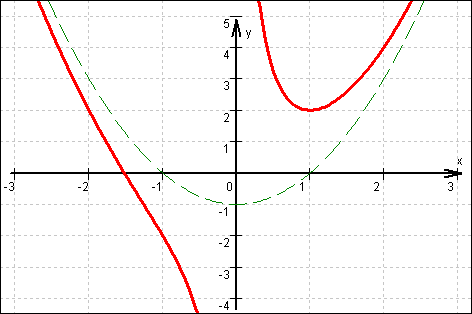
a) Winkelhalbierende des 1. und 3. Quadranten: y = x
 z. B. f(x) = x +
z. B. f(x) = x + 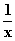 =
= 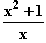 , denn:
f(–x) = –x –
, denn:
f(–x) = –x – 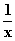 = –f(x),
d. h. Gf ist punktsymmetrisch bzgl. O.
Graph:
= –f(x),
d. h. Gf ist punktsymmetrisch bzgl. O.
Graph:
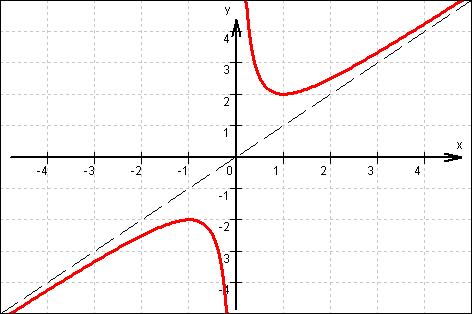 b) Wegen der Achsensymmetrie zur y–Achse dürfen keine
ungeraden x–Potenzen vorkommen.
Ansatz: f(x) = 1 +
b) Wegen der Achsensymmetrie zur y–Achse dürfen keine
ungeraden x–Potenzen vorkommen.
Ansatz: f(x) = 1 + 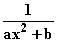 hat die waagrechte Asymptote y = 1
und ihr Graph ist achsensymmetrisch zur y–Achse.
Damit ihr Graph den HOP(0|–1) hat, muss gelten:
I. f(0) = –1
hat die waagrechte Asymptote y = 1
und ihr Graph ist achsensymmetrisch zur y–Achse.
Damit ihr Graph den HOP(0|–1) hat, muss gelten:
I. f(0) = –1  1 +
1 + 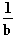 = –1
= –1  b = –0,5
II. f '(0) = 0 f '(x) =
b = –0,5
II. f '(0) = 0 f '(x) = 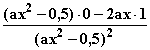 =
= 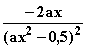 = 0
= 0
 x = 0. Bedingung II. ist also erfüllt.
III. f ''(0) < 0
f ''(x) =
x = 0. Bedingung II. ist also erfüllt.
III. f ''(0) < 0
f ''(x) = 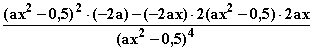 =
= 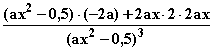 =
= 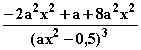 =
= 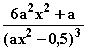
 f '' (0) = –8a < 0, wenn a > 0, also z. B. wenn a = 1.
Damit lautet die Funktion f z. B.: f(x) = 1 +
f '' (0) = –8a < 0, wenn a > 0, also z. B. wenn a = 1.
Damit lautet die Funktion f z. B.: f(x) = 1 + 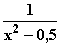 =
= 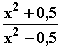 Graph:
Graph:
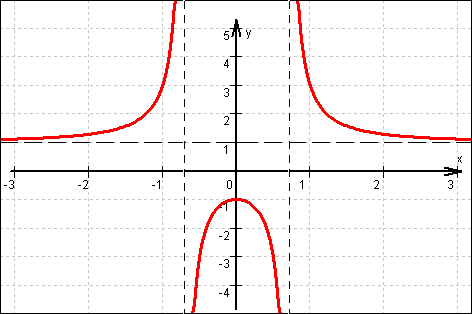 c) Gf hat genau dann keine senkrechte Asymptote, wenn f keine
Definitionslücke besitzt. Die Nennerfunktion n(x) darf also keine
Nullstellen haben, also z. B. n(x) = x
c) Gf hat genau dann keine senkrechte Asymptote, wenn f keine
Definitionslücke besitzt. Die Nennerfunktion n(x) darf also keine
Nullstellen haben, also z. B. n(x) = x + 1.
Die zur Parabel gehörige Funktion heiße p(x).
Damit die Graphen von f und p sich bei x = 2 berühren, muss
gelten:
I. f(2) = p(2) = 0, d. h. x = 2 muss eine Nullstelle der Zähler-
funktion z(x) sein.
Demnach ergibt sich für f der Ansatz: f(x) =
+ 1.
Die zur Parabel gehörige Funktion heiße p(x).
Damit die Graphen von f und p sich bei x = 2 berühren, muss
gelten:
I. f(2) = p(2) = 0, d. h. x = 2 muss eine Nullstelle der Zähler-
funktion z(x) sein.
Demnach ergibt sich für f der Ansatz: f(x) = 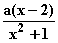 II. f '(2) = p'(2) = –4
f '(x) =
II. f '(2) = p'(2) = –4
f '(x) = 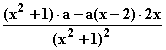 =
= 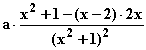 =
= 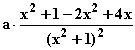 =
= 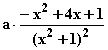
 f '(2) = =
f '(2) = = 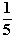 a = –4
a = –4  a = –20
Damit lautet die Funktion f z. B.: f(x) =
a = –20
Damit lautet die Funktion f z. B.: f(x) = 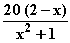 Graphen von f und p:
Graphen von f und p:
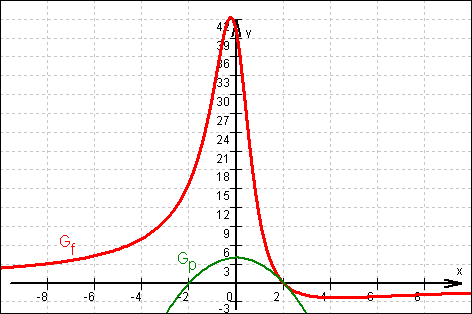 d) 1. Versuch: f(x) = x + 1 +
d) 1. Versuch: f(x) = x + 1 + 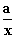 Der Graph hat die geforderten Asymptoten.
Damit die schiefe Asymptote bei x = 1 geschnitten
wird, muss gelten:
1 + 1 + a = 1 + 1, also a = 0, was nicht möglich ist.
2. Versuch: f(x) = x + 1 +
Der Graph hat die geforderten Asymptoten.
Damit die schiefe Asymptote bei x = 1 geschnitten
wird, muss gelten:
1 + 1 + a = 1 + 1, also a = 0, was nicht möglich ist.
2. Versuch: f(x) = x + 1 + 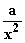 Der Graph hat die geforderten Asymptoten.
Damit die schiefe Asymptote bei x = 1 geschnitten
wird, muss gelten:
1 + 1 + a = 1 + 1, also a = 0, was nicht möglich ist.
3. Versuch: f(x) = x + 1 +
Der Graph hat die geforderten Asymptoten.
Damit die schiefe Asymptote bei x = 1 geschnitten
wird, muss gelten:
1 + 1 + a = 1 + 1, also a = 0, was nicht möglich ist.
3. Versuch: f(x) = x + 1 + 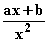 Der Graph hat die geforderten Asymptoten.
Damit die schiefe Asymptote bei x = 1 geschnitten
wird, muss gelten:
1 + 1 + a + b = 1 + 1
Der Graph hat die geforderten Asymptoten.
Damit die schiefe Asymptote bei x = 1 geschnitten
wird, muss gelten:
1 + 1 + a + b = 1 + 1  b = –a,
also z. B. a = 1, b = –1
Damit ist eine mögliche Funktion f gefunden:
f(x) = x + 1 +
b = –a,
also z. B. a = 1, b = –1
Damit ist eine mögliche Funktion f gefunden:
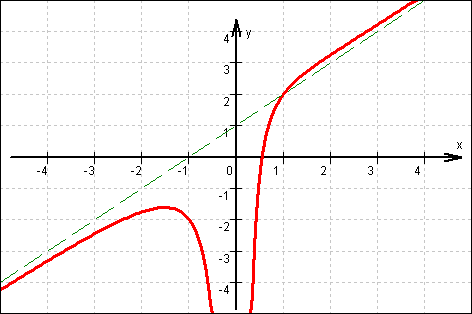
f(x) = x + 1 + 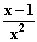 =
= 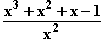 Graph:
Graph:
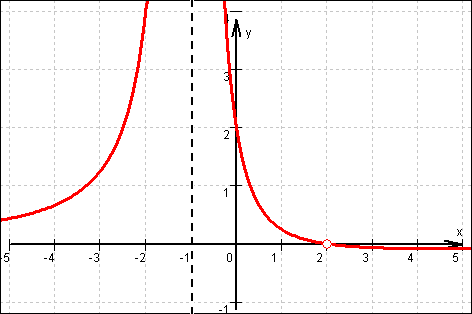
 e) Damit der Graph im Punkt (2|0) unterbrochen ist, muss der
Linearfaktor (x – 2) aus f herauskürzbar sein.
Zunächst wird der gekürzte Funktionsterm
e) Damit der Graph im Punkt (2|0) unterbrochen ist, muss der
Linearfaktor (x – 2) aus f herauskürzbar sein.
Zunächst wird der gekürzte Funktionsterm 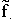 betrachtet:
Dieser muss die Nullstelle x = 2 und die doppelte Polstelle
x = –1 besitzen:
betrachtet:
Dieser muss die Nullstelle x = 2 und die doppelte Polstelle
x = –1 besitzen:
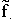 (x) =
(x) = 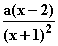 Der Faktor a ist noch nötig, um das Verhalten von
Der Faktor a ist noch nötig, um das Verhalten von 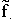 bei x = –1
zu berücksichtigen:
x
bei x = –1
zu berücksichtigen:
x  –1
–1 
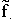 (x)
(x)  –3a·∞
–3a·∞ 
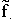 (x)
(x)  +∞, wenn a < 0,
also z. B. a = –1.
Um jetzt noch die Nullstelle x = 2 zu einer hebbaren Lücke zu
machen, wird
+∞, wenn a < 0,
also z. B. a = –1.
Um jetzt noch die Nullstelle x = 2 zu einer hebbaren Lücke zu
machen, wird 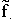 um den Faktor (x – 2) erweitert.
Damit lautet die Funktion f z. B.: f(x) =
um den Faktor (x – 2) erweitert.
Damit lautet die Funktion f z. B.: f(x) = 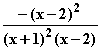 Graph:
Graph:
 f) TIP(1|2)
f) TIP(1|2)  Gf
Gf  I. f(1) = 2;
II. f ' (1) = 0;
III. f ''(1) > 0
Also sind mindestens 2 Parameter nötig.
Ansatz f(x) = x
I. f(1) = 2;
II. f ' (1) = 0;
III. f ''(1) > 0
Also sind mindestens 2 Parameter nötig.
Ansatz f(x) = x – 1 +
– 1 + 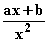 = x
= x – 1 +
– 1 + 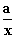 +
+ 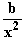 Der Graph einer solchen Funktion hat die geforderte
asymptotische Kurve.
Zu Bedingung I.:
1 – 1 + a + b = 2
Der Graph einer solchen Funktion hat die geforderte
asymptotische Kurve.
Zu Bedingung I.:
1 – 1 + a + b = 2  b = 2 – a
Zu Bedingung II.:
f '(x) = 2x –
b = 2 – a
Zu Bedingung II.:
f '(x) = 2x – 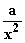 –
– 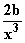
 2 – a – 2b = 0
2 – a – 2b = 0

 b = 0; a = 2
Probe mit III.:
f ''(x) = 2 +
b = 0; a = 2
Probe mit III.:
f ''(x) = 2 + 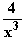
 f ''(1) = 6 > 0, d. h. III. ist auch erfüllt.
Damit lautet die Funktion f z. B.: f(x) = x
f ''(1) = 6 > 0, d. h. III. ist auch erfüllt.
Damit lautet die Funktion f z. B.: f(x) = x – 1 +
– 1 + 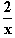 =
= 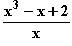 Graph:
Graph: