Übungsblatt Rationale Funktionen
Lösungen zu Aufgabe 9
a) f(–x) = 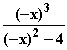 = –
= – 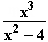 = –f(x)
= –f(x)  Gf ist punktsymmetrisch bzgl. des Koordinatenursprungs.
b) Definitionslücken: x
Gf ist punktsymmetrisch bzgl. des Koordinatenursprungs.
b) Definitionslücken: x – 4 = 0
– 4 = 0  x
x

 = ±2
Dreifache Nullstelle: x = 0
Verhalten von f an den Definitionslücken:
= ±2
Dreifache Nullstelle: x = 0
Verhalten von f an den Definitionslücken:
| | x < | –2 | < x < | 0 | < x < | 2 | < x |
|---|
| Zähler von f | – | – | – | 0 | + | + | + |
| Nenner von f | + | 0 | – | – | – | 0 | + |
| f(x) | –  | –∞ / +∞ | 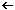 + + | 0 | –  | –∞ / +∞ |  + + |
c) Nach b) gibt es zwei senkrechte Asymptoten mit den Gleichungen
x = –2 und x = 2.
Außerdem gibt es eine schiefe Asymptote, da der Zählergrad von f
um 1 größer ist als der Nennergrad.
Ihre Gleichung wird durch Polynomdivision ermittelt:
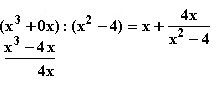
 Gleichung der schiefen Asymptote: y = x
d) f '(x) =
Gleichung der schiefen Asymptote: y = x
d) f '(x) = 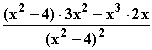 =
= 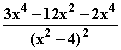 =
= 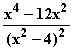 = 0
= 0
 x
x –12x
–12x = 0
= 0  x
x (x
(x –12) = 0
–12) = 0  x
x

 = 0; x
= 0; x

 = ±
= ±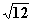 = ±2
= ±2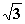 Der Nenner von f ' ist in IDf immer positiv. Also hängt das
Vorzeichen von f ' nur von seinem Zähler ab.
x
Der Nenner von f ' ist in IDf immer positiv. Also hängt das
Vorzeichen von f ' nur von seinem Zähler ab.
x

 = 0 ist doppelte Nullstelle von f '
= 0 ist doppelte Nullstelle von f '  TEP(0|0)
Bei x
TEP(0|0)
Bei x = 2
= 2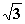 wechselt das Zählervorzeichen von – nach +
wechselt das Zählervorzeichen von – nach +  TIP(2
TIP(2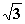 | 3
| 3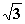 )
Punktsymmetrie von G
)
Punktsymmetrie von G bzgl. O
bzgl. O  HOP(–2
HOP(–2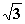 | –3
| –3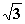 )
e)
)
e) 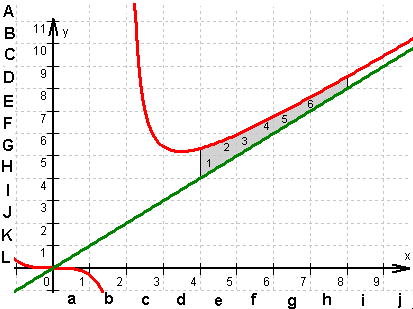 In der Grafik ist die durch das Integral
In der Grafik ist die durch das Integral 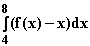 beschriebene
Fläche grau hervorgehoben. Diese Fläche lässt sich grob in halbe
Planquadrate mit dem Flächeninhalt 0,5 FE. zerlegen.
Da sich etwas mehr als 6 halbe Planquadrate ergeben, resultiert
für das Integral ein Wert von ca. 3.
f) f(x) =
beschriebene
Fläche grau hervorgehoben. Diese Fläche lässt sich grob in halbe
Planquadrate mit dem Flächeninhalt 0,5 FE. zerlegen.
Da sich etwas mehr als 6 halbe Planquadrate ergeben, resultiert
für das Integral ein Wert von ca. 3.
f) f(x) = 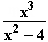 ; f
; f (x) =
(x) = 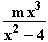 = m·f(x)
Für m > 0 gilt das Vorstehende mit der Abwandlung, dass die
schiefe Asymptote jetzt die Gleichung y = m·x hat und auch die
Ordinaten der Extrempunkte noch mit m multipliziert werden.
Für m > 1 sind alle Ordninaten im Vergleich zu denen der
Funktion f gestreckt, für 0 < m < 1 gestaucht.
Für m < 0 ist der Graph im Vergleich zu m > 0 an der x–Achse
gespiegelt, d. h., das Verhalten an den Definitionslücken dreht sich
um, und die Extrempunkte tauschen ihre Art.
= m·f(x)
Für m > 0 gilt das Vorstehende mit der Abwandlung, dass die
schiefe Asymptote jetzt die Gleichung y = m·x hat und auch die
Ordinaten der Extrempunkte noch mit m multipliziert werden.
Für m > 1 sind alle Ordninaten im Vergleich zu denen der
Funktion f gestreckt, für 0 < m < 1 gestaucht.
Für m < 0 ist der Graph im Vergleich zu m > 0 an der x–Achse
gespiegelt, d. h., das Verhalten an den Definitionslücken dreht sich
um, und die Extrempunkte tauschen ihre Art.
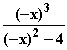 = –
= – 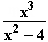 = –f(x)
= –f(x)  Gf ist punktsymmetrisch bzgl. des Koordinatenursprungs.
b) Definitionslücken: x
Gf ist punktsymmetrisch bzgl. des Koordinatenursprungs.
b) Definitionslücken: x – 4 = 0
– 4 = 0  x
x

 = ±2
Dreifache Nullstelle: x = 0
Verhalten von f an den Definitionslücken:
= ±2
Dreifache Nullstelle: x = 0
Verhalten von f an den Definitionslücken:
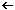 +
+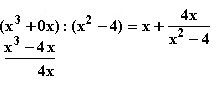
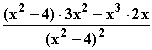 =
= 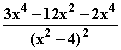 =
= 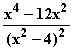 = 0
= 0
 –12x
–12x
 = ±
= ±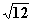 = ±2
= ±2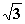 Der Nenner von f ' ist in IDf immer positiv. Also hängt das
Vorzeichen von f ' nur von seinem Zähler ab.
x
Der Nenner von f ' ist in IDf immer positiv. Also hängt das
Vorzeichen von f ' nur von seinem Zähler ab.
x bzgl. O
bzgl. O  In der Grafik ist die durch das Integral
In der Grafik ist die durch das Integral 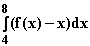 beschriebene
Fläche grau hervorgehoben. Diese Fläche lässt sich grob in halbe
Planquadrate mit dem Flächeninhalt 0,5 FE. zerlegen.
Da sich etwas mehr als 6 halbe Planquadrate ergeben, resultiert
für das Integral ein Wert von ca. 3.
f) f(x) =
beschriebene
Fläche grau hervorgehoben. Diese Fläche lässt sich grob in halbe
Planquadrate mit dem Flächeninhalt 0,5 FE. zerlegen.
Da sich etwas mehr als 6 halbe Planquadrate ergeben, resultiert
für das Integral ein Wert von ca. 3.
f) f(x) =  (x) =
(x) = 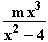 = m·f(x)
Für m > 0 gilt das Vorstehende mit der Abwandlung, dass die
schiefe Asymptote jetzt die Gleichung y = m·x hat und auch die
Ordinaten der Extrempunkte noch mit m multipliziert werden.
Für m > 1 sind alle Ordninaten im Vergleich zu denen der
Funktion f gestreckt, für 0 < m < 1 gestaucht.
Für m < 0 ist der Graph im Vergleich zu m > 0 an der x–Achse
gespiegelt, d. h., das Verhalten an den Definitionslücken dreht sich
um, und die Extrempunkte tauschen ihre Art.
= m·f(x)
Für m > 0 gilt das Vorstehende mit der Abwandlung, dass die
schiefe Asymptote jetzt die Gleichung y = m·x hat und auch die
Ordinaten der Extrempunkte noch mit m multipliziert werden.
Für m > 1 sind alle Ordninaten im Vergleich zu denen der
Funktion f gestreckt, für 0 < m < 1 gestaucht.
Für m < 0 ist der Graph im Vergleich zu m > 0 an der x–Achse
gespiegelt, d. h., das Verhalten an den Definitionslücken dreht sich
um, und die Extrempunkte tauschen ihre Art.