BAYERISCHES STAATSMINISTERIUM FÜR UNTERRICHT UND KULTUS
Lehrpläne für die Berufsoberschule
Unterrichtsfach: Mathematik (Nichttechnik)
Jahrgangsstufen 12 und 13
Die Lehrpläne wurden mit KMBek vom 5. August 2003 Nr. VII.7-5 S 9410W1-6-7.66823 in Kraft gesetzt.
Die Lehrpläne der Vorstufe treten zum Beginn des Schuljahres 2003/04 in Kraft, die Lehrpläne für die Jahrgangsstufen 12 zum Beginn des
Schuljahres 2004/05, die Lehrpläne für die Jahrgangsstufen 13 zum Beginn des Schuljahres 2005/06. Sie ersetzen die bisher gültigen Lehr-
pläne.
INHALTSVERZEICHNIS
Seite
EINFÜHRUNG
1 Vorbemerkung zum Aufbau und zur Verbindlichkeit der Lehrpläne
1
2 Schulartprofil Berufsoberschule
2
3
Stundentafel
3
4 Übersicht über die Fächer und Lerngebiete
3
LEHRPLÄNE
Mathematik (Nichttechnik)
5
ANLAGE
Mitglieder der Lehrplankommission
21
Berufsoberschule
Mathematik - Nichttechnik
Seite 1
EINFÜHRUNG
1 Vorbemerkung zum Aufbau und zur Verbindlichkeit der Lehrpläne
Die folgenden Lehrpläne beschreiben die Bildungs- und Erziehungsaufgaben der Berufsoberschule auf drei Ebenen.
Die erste Ebene umfasst das Schulartprofil und erläutert den Bildungsauftrag der Schulart allgemein. Die zweite Ebene ist die der Fachprofile. Das
Fachprofil charakterisiert den Unterricht eines bestimmten Fachs im Ganzen, indem es übergeordnete Ziele beschreibt, didaktische Entscheidungen be-
gründet und fachlich-organisatorische Hinweise (z. B. auf fachübergreifenden Unterricht) gibt. Die Fachlehrpläne bilden die dritte Ebene. Sie enthal-
ten jeweils eine Übersicht über die Lerngebiete sowie eine nach Jahrgangsstufen geordnete Darstellung der Lernziele, Lerninhalte und Hinweise zum
Unterricht.
Die Lernziele geben Auskunft über die Art der personalen Entwicklung, die bei den Schülerinnen und Schülern gefördert wird. Die Lernziele sind frei
formuliert. Die jeweils gewählte Formulierung will deutlich machen, mit welchen der vier didaktischen Schwerpunkte – Wissen, Können und Anwen-
den, produktives Denken und Gestalten sowie Wertorientierung – die beschriebenen Entwicklungsprozesse in Verbindung stehen. Den Lernzielen sind
Lerninhalte zugeordnet. Diese stellen die fachspezifischen Lerngegenstände des Unterrichts dar.
Die in den drei Lehrplanebenen aufgeführten Ziele und Inhalte bilden zusammen mit fächerübergreifenden Bildungs- und Erziehungsaufgaben 1, den
einschlägigen Artikeln des Grundgesetzes für die Bundesrepublik Deutschland, der Verfassung des Freistaates Bayern und des Bayerischen Gesetzes
über das Erziehungs- und Unterrichtswesen die verbindliche Grundlage für den Unterricht und die Erziehungsarbeit.
Die Fachlehrpläne stellen Lernziele und Lerninhalte systematisch dar. Ihre konkrete Abfolge im Unterricht ergibt sich aus dem jeweiligen Unterrichts-
gegenstand, für den u. U. verschiedene Lernziele des Lehrplans kombiniert werden, aus der gewählten Unterrichtsmethode und der Absprache der
Lehrkräfte.
Die Hinweise zum Unterricht sowie die Zeitrichtwerte dienen der Orientierung oder Abgrenzung und sind nicht verbindlich. Die Freiheit der Metho-
denwahl im Rahmen der durch die Lernziele ausgedrückten didaktischen Absichten ist dadurch nicht eingeschränkt. Die Lehrpläne sind grundsätzlich
so angelegt, dass ein ausreichender pädagogischer Freiraum bleibt, damit spezifische Interessen der Schülerinnen und Schüler, aktuelle Themen sowie
öffentliche bzw. regionale Gegebenheiten aufgegriffen werden können.
1
Z. B. dargestellt in: Staatsinstitut für Schulpädagogik und Bildungsforschung, Abt. Berufliche Schulen (Hrsg.), Bildungs- und Erziehungsaufgaben an Berufsschulen und Berufs-
fachschulen, München 1996
Berufsoberschule
Mathematik - Nichttechnik
Seite 2
2
Schulartprofil
Die Berufsoberschule führt Schülerinnen und Schüler mit mittlerem Schulabschluss und Berufsausbildung oder einschlägiger Berufserfahrung in zwei
Jahren zur fachgebundenen Hochschulreife, mit dem Nachweis ausreichender Kenntnisse in einer zweiten Fremdsprache (auf dem Niveau der 10. Klas-
se des Gymnasiums) zur allgemeinen Hochschulreife. Durch die erfolgreiche Teilnahme an der fakultativen Fachhochschulreifeprüfung können sie
nach einem Jahr die Fachhochschulreife erwerben. Entsprechend ihrer beruflichen Qualifikation werden die Schülerinnen und Schüler vier Ausbil-
dungsrichtungen zugeordnet: Technik, Wirtschaft, Sozialwesen, Agrarwirtschaft.
Zum Erwerb der Studierfähigkeit werden die Schülerinnen und Schüler in die Lage versetzt, anspruchsvolle theoretische Erkenntnisse nachzuvollzie-
hen, komplizierte Zusammenhänge zu durchschauen und verständlich darzustellen. Die Schülerinnen und Schüler erwerben hohe kommunikative
Kompetenz in der deutschen Sprache, entwickeln ein hohes Sprach- und Literaturverständnis und beherrschen eine Fremdsprache auf anspruchsvollem
Niveau. Sie besitzen geschichtliches Bewusstsein und soziale Reife und gehen sicher mit komplexen mathematischen und naturwissenschaftlichen
Problemen um. Komplexe moderne Informations- und Kommunikationsmittel nutzen sie kompetent und verantwortungsvoll. Die Schüler und Schüle-
rinnen sind in der Lage, sich mit tiefer gehenden Problemstellungen der jeweiligen Fächer auseinander zu setzen.
Der Unterricht greift die im Berufsleben erworbenen Kenntnisse, Fähigkeiten und Erfahrungen der jungen Erwachsenen auf und erweitert sie – beste-
hende Unterschiede ausgleichend – gemäß den Bildungszielen der Schulart. Die Lehrkräfte geben den Schülerinnen und Schülern Gelegenheit, im fä-
cherübergreifenden und projektorientierten Arbeiten die bereits erworbenen Arbeitstugenden zu entfalten. Die Schülerinnen und Schüler werden zum
selbstständigen Wissenserwerb und zum eigenständigen Urteilen angeleitet. Dies verlangt eigenverantwortliches Lösen komplexer Aufgaben und för-
dert dadurch Flexibilität und Kreativität. Die Schülerinnen und Schüler bauen ihre fachlichen Kompetenzen aus, entwickeln ein umfassendes Problem-
bewusstsein sowie Einstellungen und Haltungen, die auf verantwortliches Handeln in der Gemeinschaft ausgerichtet sind.
Die Verwirklichung der Bildungsziele setzt bei den Schülerinnen und Schülern grundlegende Kenntnisse in den Fächern der jeweiligen Ausbildungs-
richtung voraus. Für einen erfolgreichen Schulabschluss sind eine hohe Bereitschaft, sich auf geistige und ethische Herausforderungen einzulassen, eine
hohe Lernmotivation, große Ausdauer, geistige Beweglichkeit und die Fähigkeit, selbstständig und mit anderen zu arbeiten, notwendig.
Berufsoberschule
Mathematik - Nichttechnik
Seite 3
3 Stundentafel
Den Lehrplänen liegt die Stundentafel der Schulordnung für die Berufsoberschulen in Bayern (BOSO) in der jeweils gültigen Fassung zugrunde.
4 Übersicht über die Lerngebiete
Die Zahlen in Klammern geben Zeitrichtwerte an, d. h. die für das betreffende Lerngebiet empfohlene Zahl von Unterrichtsstunden.
Jahrgangsstufe 12
Analysis
12.1 Grundbegriffe bei reellen Funktionen (37)
12.2 Grenzwert und Stetigkeit
(10)
12.3 Differenzialrechnung
(40)
12.4 Integralrechnung
(12)
Stochastik
12.5 Zufallsexperiment und Ereignis
(15)
12.6 Relative Häufigkeit und Wahrschein-
lichkeit
(14)
12.7 Berechnung von Wahrscheinlich-
keiten
(12)
12.8 Zufallsgröße und Wahrscheinlich-
keitsverteilung
(16)
12.9 Testen von Hypothesen
( 9)
165
Berufsoberschule
Mathematik - Nichttechnik
Seite 4
Jahrgangsstufe 13
Analysis
13.1 Eigenschaften gebrochen-rationaler
Funktionen
(12)
13.2 Ableitungsregeln
( 8)
13.3 Kurvendiskussion gebrochen-ratio-
naler Funktionen
(15)
13.4 Kurvendiskussion von Exponential-
und Logarithmusfunktionen
(15)
13.5 Kurvendiskussion zusammengesetz-
ter Exponential- und Logarithmus-
funktionen
(36)
Lineare Algebra und Analytische Geometrie
13.6 Vektoren im
IR
2
und IR
3
(12)
13.7 Matrizen
( 9)
13.8 Lineare Unabhängigkeit von Vek-
toren im
IR
2
und IR
3
; lineare
Gleichungssysteme
(23)
13.9 Leontief-Modell
(12)
13.10 Geometrische Anwendungen
im IR
3
(23)
165
Berufsoberschule Ausbildungsrichtung Nichttechnik
Mathematik
Seite 5
LEHRPLÄNE
MATHEMATIK
Fachprofil: Die Mathematik hat ihren Ursprung im Interesse der Menschen, Dinge der Erfahrungswelt und ihre gegenseitigen Beziehungen
quantitativ zu erfassen. Zählen, Messen, Simulieren, Rechnen und Berechnen, Zeichnen und Konstruieren sind für planendes
Handeln von großer Bedeutung. Damit verbunden ist der Drang nach zweckfreier Erkenntnis, der wesentlich die Entwicklung
der Mathematik bestimmt: Probleme der Praxis geben ebenso wie theoretische Fragen Anlass zur Erforschung grundlegender
Zusammenhänge; aus der Wechselwirkung mit den Erfahrungswissenschaften ergeben sich für beide Bereiche vertiefte Einsich-
ten. Die Mathematik ist heute ein weit verzweigtes Gebiet, das umfangreiches Wissen und vielfältige Verfahren bereitstellt. Da-
mit trägt sie zur wissenschaftlichen Erschließung unserer Wirklichkeit und zur Gestaltung unserer Umwelt entscheidend bei.
Ziel des Mathematikunterrichts ist es, den Schülerinnen und Schülern die Welt der Mathematik näher zu bringen und ihnen die
nötigen Kenntnisse und Arbeitsweisen zu vermitteln, um Zusammenhänge mathematisch erschließen zu können. Der Unterricht
macht mit einigen grundlegenden Ideen und Formen mathematischer Betrachtung und Tätigkeit vertraut. Die Schülerinnen und
Schüler erfahren dabei eine intensive Schulung des Denkens: Die Entwicklung klarer Begriffe und Vorstellungen, eine folge-
richtige Gedankenführung und systematisches induktives oder deduktives Vorgehen sind typische Erfordernisse und Kennzei-
chen mathematischen Arbeitens. Entsprechende Fähigkeiten auszubilden ist eine durchgängige Aufgabe im Mathematikunter-
richt und bringt Gewinn über das mathematische Fachgebiet hinaus.
Ein weiteres Unterrichtsziel ist der sorgfältige Gebrauch der Sprache: Eindeutigkeit, Widerspruchsfreiheit und Vollständigkeit
bei der Verbalisierung mathematischer Sachverhalte sind für deren gedankliche Durchdringung unerlässlich.
Zunehmend von Bedeutung ist die Mathematik für viele Anwendungsgebiete. Neben Naturwissenschaft und Technik verwenden
auch die Wirtschafts- und Sozialwissenschaften vermehrt mathematische Methoden. An geeigneten Aufgaben und Projekten aus
diesen Bereichen – mit Schwerpunkt auf den ausbildungsrichtungsspezifischen Profilfächern – lernen die Schülerinnen und
Schüler, Sachzusammenhänge mathematisch zu erfassen, entsprechende Modellvorstellungen zu entwickeln und ggf. mit geeig-
neten informationstechnischen Werkzeugen zu behandeln. Damit will der Mathematikunterricht in der beruflichen Oberstufe den
Schülerinnen und Schülern in ausreichendem Maß die für Studium und Beruf notwendigen Voraussetzungen vermitteln. Der
grundbildende Aspekt der Mathematik steht dabei im Vordergrund.
Berufsoberschule Ausbildungsrichtung Nichttechnik
Mathematik
Seite 6
Jahrgangsstufe 12
Lerngebiete:
Analysis
12.1 Grundbegriffe bei reellen Funktionen
37 Std.
12.2 Grenzwert und Stetigkeit
10 Std.
12.3 Differenzialrechnung
40 Std.
12.4 Integralrechnung
12 Std.
Stochastik
12.5 Zufallsexperiment und Ereignis
15 Std.
12.6 Relative Häufigkeit und Wahrscheinlichkeit
14 Std.
12.7 Berechnung von Wahrscheinlichkeiten
12 Std.
12.8 Zufallsgröße und Wahrscheinlichkeitsverteilung
16 Std.
12.9 Testen von Hypothesen
9 Std.
165 Std.
LERNINHALTE
HINWEISE ZUM UNTERRICHT
Analysis
12.1 Grundbegriffe bei reellen Funktionen
37 Std.
12.1.1 Grundlagen
Die grundlegenden Begriffe zum The-
mengebiet sollen von den Schülerinnen
und Schülern teils wiederholt, teils neu
erarbeitet werden. Dabei sollen sie die
Zahlenmengen IN, Z, Q, IR und ihre Eigen-
schaften
Auf die unterschiedliche Verwendung des Symbols IN
soll hingewiesen werden.
Unterscheidung zwischen exakter und näherungsweiser
Angabe einer reellen Zahl
Berufsoberschule Ausbildungsrichtung Nichttechnik
Mathematik
Seite 7
zugehörigen Termumformungen durch-
führen können. Von Anfang an sollen sie
zudem auf die korrekte Verwendung der
Fachterminologie achten. Schülerinnen
und Schüler mit geringen Vorkenntnissen
erhalten Anregungen, wie sie ihre Defizite
durch selbstständige häusliche Arbeit be-
heben können. Eine ausführliche Wieder-
holung algebraischer Grundlagen aus der
Mittelstufe ist hier nicht möglich.
Reelle Funktionen:
Abbildungsvorschrift, Funktionsterm, Funkti-
onsgleichung, Definitions- und Wertemenge,
Funktionsgraph
Schnittpunkte mit den Koordinatenachsen
Lineare Funktionen, quadratische Funktionen
auch mit Parameter
Lineare und quadratische Ungleichungen
Potenzfunktionen mit Exponenten
n 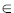
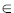
{3, 4, –1}
Anwendungsbeispiele siehe auch 12.1.3
Lösung z. B. mit Hilfe von Funktionsgraphen oder mit
Vorzeichentabellen
12.1.2 Ganzrationale Funktionen
Anhand der ganzrationalen Funktionen
(Polynomfunktionen) werden weitere
grundlegende Begriffe zu Funktionen
wiederholt bzw. neu erarbeitet. Dabei sol-
len die Schülerinnen und Schüler auch die
zugehörigen Termumformungen sicher
beherrschen lernen.
Verknüpfung von Funktionen: Summe, Diffe-
renz und Produkt
Nullstellenbestimmung unter Verwendung von
Polynomdivision und Substitution
Faktorisierung des Funktionsterms und Viel-
fachheit der Nullstellen
Symmetrie des Funktionsgraphen
Auswirkungen auf den Funktionsgraphen
Auch Schnittprobleme behandeln
Hier sollen auch Aufgaben mit Parameter bearbeitet
werden.
Nur Achsensymmetrie zur y-Achse und Punktsymmetrie
zum Ursprung behandeln
Computereinsatz zur Veranschaulichung
12.1.3 Mathematische Modellbildung
Die Schülerinnen und Schüler lernen ma-
thematische Modelle zur Beschreibung
realer Zusammenhänge kennen. Dabei
werden auch die Grenzen solcher Modelle
diskutiert.
Anwendungsbeispiele mit ganzrationalen
Funktionen
Abschnittsweise definierte Funktionen
Z. B. Stromtariffunktion, Kostenfunktion, Erlösfunktion
Aufstellen einer ganzrationalen Funktion aus Wertepaa-
ren im Sachzusammenhang
Z. B. Einkommensteuerfunktion, Telefongebührenfunk-
tion
Berufsoberschule Ausbildungsrichtung Nichttechnik
Mathematik
Seite 8
12.2 Grenzwert und Stetigkeit
10 Std.
12.2.1 Grenzwert
Der für die Analysis fundamentale Begriff
des Grenzwerts wird erarbeitet und an ver-
schiedenartigen Beispielen verdeutlicht.
Anhand gebrochen-rationaler Funktionen
werden Konvergenz und Divergenz veran-
schaulicht und der Differenzialquotient
vorbereitet. Die Anwendung der Grenz-
wertsätze erleichtert die rechnerischen
Untersuchungen und vermittelt Sicherheit
in der Bestimmung von Grenzwerten.
Quotient von Funktionen
Grenzwert einer Funktion für x
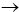 ±
±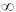
bzw.
x 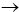 x0
x0
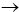 x0
x0.
Grenzwertsätze für Summe, Differenz, Produkt
und Quotient von Funktionen
Zähler- und Nennerpolynom sollen höchstens Grad 2
besitzen.
Die Grenzwertberechnungen dienen der Vorbereitung
des Differenzialquotienten.
Es genügt, die Grenzwertsätze plausibel zu machen.
Die grafische Darstellung gebrochen-rationaler Funktio-
nen dient zur Veranschaulichung, sollte aber nicht ge-
prüft werden.
Die Begriffe Unendlichkeitsstelle, behebbare Definiti-
onslücke und Asymptote werden nur anschaulich ver-
wendet.
12.2.2 Stetigkeit
Die Schülerinnen und Schüler erfassen
den Begriff Stetigkeit einer Funktion an
einer Stelle sowie in einem Intervall und
können Stetigkeitsuntersuchungen an ein-
fachen Beispielen durchführen. Sie lernen
Eigenschaften von Funktionen kennen, die
auf abgeschlossenen Intervallen stetig
sind.
Stetigkeit einer Funktion an einer Stelle
Stetigkeit in einem Intervall
Zwischenwertsatz
Nullstellensatz
Extremwertsatz
Der Begriff der Stetigkeit soll anschaulich verdeutlicht
werden, Beispiele für unstetige Funktionen ergeben sich
aus Lernziel 12.1.3.
Auf Stetigkeitsuntersuchungen mit Parameter wird ver-
zichtet.
Die Sätze werden anschaulich vermittelt.
Eine nummerische Methode zur Nullstellenermittlung
sollte exemplarisch durchgeführt werden. Hierbei eignet
sich der Einsatz von Computerprogrammen.
12.3 Differenzialrechnung
40 Std.
12.3.1 Anhand einfacher Funktionen er-
Differenzenquotient
Berufsoberschule Ausbildungsrichtung Nichttechnik
Mathematik
Seite 9
fahren die Schülerinnen und Schü-
ler die Grundbegriffe der Differen-
zialrechnung. Sie erlernen das Auf-
stellen der Gleichung einer Tangen-
te im Punkt eines Graphen und ler-
nen den Begriff der Ableitungs-
funktion kennen. Neben der geo-
metrischen Betrachtung (Sekante,
Tangente) erkennen sie die Ablei-
tung als lokale Änderungsrate einer
Größe.
Differenzialquotient
Differenzierbarkeit
Ableitung einer Funktion an einer Stelle und
Bestimmung der Ableitungsfunktionen für
f(x) = c, f(x) = x
,
f(x) = x2
und
f(x) = x3
unter Verwendung des Differenzenquotienten
Tangente
Unterschiedliche Schreibweisen:

Änderungsrate einer Größe
Zusammenhang zwischen den Graphen von
Funktion und Ableitungsfunktion
Es sollen keine abschnittsweise definierten Funktionen
mit dem Differenzenquotienten untersucht werden.
Die Bedeutung der Ableitung als lokale Änderungsrate
einer Größe lässt sich durch folgende Beispiele verdeut-
lichen:
Momentangeschwindigkeit, Momentanbeschleunigung,
Entwicklung von Aktienkursen, Populationen u. Ä.
Durch Darstellung der Graphen von Funktion und Ablei-
tungsfunktion mit Hilfe des Computers kann die Ände-
rung einzelner Parameter und deren Auswirkung an-
schaulich behandelt werden.
12.3.2 Die Schülerinnen und Schüler er-
fahren, dass die Ableitungsregeln
die Berechnung von Ableitungen
erleichtern.
Ableitung einer Funktion mit konstantem Fak-
tor
Summenregel
Ableitung von
f(x) = xn
mit n
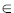
IN
Ableitung der Polynomfunktionen
Auf Produkt- und Kettenregel wird verzichtet.
12.3.3 Die Schülerinnen und Schüler er-
kennen den Zusammenhang zwi-
Stetigkeit als notwendige Voraussetzung für
Differenzierbarkeit
Die Existenz von
x 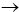 x0
x0
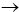 x0
x0lim f '(x)
ist hinreichend für die Dif-
Berufsoberschule Ausbildungsrichtung Nichttechnik
Mathematik
Seite 10
schen Stetigkeit und Differenzier-
barkeit einer Funktion.
Ableitung von abschnittsweise definierten
Funktionen ohne Parameter
ferenzierbarkeit einer stetigen Funktion an der Stelle x0.
12.3.4 Zunächst vergleichen die Schüle-
rinnen und Schüler die Funktions-
eigenschaften „streng monoton zu-
nehmend (abnehmend) in einem In-
tervall“ und „positive (negative)
Ableitung in einem Intervall“ mit-
einander und grenzen diese gegen-
einander ab.
Monotoniedefinition
Monotoniekriterium
Bestimmung der maximalen Intervalle in der
Definitionsmenge, in denen ein Graph streng
monoton steigt bzw. fällt
Beispiele für Probleme bei Monotonieuntersuchungen:
Die Funktion f: x 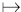 x3
x3
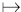 x3
x3 ist in IR streng monoton zuneh-
mend, obwohl f '(0) = 0
gilt.
Anwendungen: z. B. Anstieg der Lebenshaltungskosten
12.3.5 Die Schülerinnen und Schüler er-
fahren, dass zwischen den Funkti-
onen f '
und
f ''
ein analoger Zu-
sammenhang besteht wie zwischen
den Funktionen f und f '
, und er-
kennen die Bedeutung des Vorzei-
chens von f ''(x)
für den Verlauf
des Graphen von f.
Links- und Rechtskrümmung
Maximale Intervalle in der Definitionsmenge,
in denen der Graph links- bzw. rechtsge-
krümmt ist
Interpretation der positiven bzw. negativen zweiten Ab-
leitung als Zunahme bzw. Abnahme der Steigung eines
Funktionsgraphen
Anwendungen: z. B. Verminderung des Anstiegs der Le-
benshaltungskosten
12.3.6 Die Schülerinnen und Schüler erar-
beiten Kriterien für die Extrem-
punkte eines Graphen und deren
Art sowie Kriterien für Wende-
punkte und Terrassenpunkte.
Definition des Begriffes „Extrempunkt“ ohne
Voraussetzung der Differenzierbarkeit
Hinreichendes Kriterium für Extrempunkte bei
einmal bzw. mindestens zweimal differenzier-
baren Funktionen
Wendestellen als eigentliche Extremstellen
von f '
Hinreichendes Kriterium für Wendepunkte bei
zweimal bzw. mindestens dreimal differenzier-
baren Funktionen
Berufsoberschule Ausbildungsrichtung Nichttechnik
Mathematik
Seite 11
Randextrema, absolute Extrema
12.3.7 Die Schülerinnen und Schüler ge-
winnen Sicherheit in der Kurven-
diskussion ganzrationaler Funktio-
nen und in der Anwendung der Dif-
ferenzialrechnung. Die Grundlagen
der mathematischen Modellbildung
aus Lernziel 12.1.3 werden hier mit
Hilfe der Differenzialrechnung er-
weitert.
Kurvendiskussion von ganzrationalen Funktio-
nen und einparametrigen Funktionenscharen
Aufstellen des Funktionsterms bei vorgegebe-
nen Eigenschaften
Anwendungsaufgaben, auch Optimierungs-
probleme
Der Einfluss eines Scharparameters auf den Verlauf des
Graphen kann mit Computerprogrammen veranschau-
licht werden.
Beschränkung auf höchstens vier Bedingungen
Auf das Aufstellen von Funktionenscharen wird verzich-
tet.
12.4 Integralrechnung
12 Std.
Die Schülerinnen und Schüler lernen,
Stammfunktionen von Funktionen zu fin-
den, und berechnen damit bestimmte In-
tegrale.
Stammfunktionen einer Funktion
Unbestimmtes Integral
Definition und Eigenschaften des bestimmten
Integrals
Deutung des bestimmten Integrals als Flächen-
bilanz
Berechnung von bestimmten Integralen und
Flächeninhalten ohne Parameter
Der Zusammenhang zwischen Differenzial- und Integral-
rechnung kann über die Ableitung der Flächenfunktion
plausibel gemacht werden.
12.5 Zufallsexperiment und Ereignis
15 Std.
Der Ergebnisraum wird von den Schüle-
rinnen und Schülern als Möglichkeit er-
fahren, reale Situationen als Zufallsexpe-
rimente mathematisch zu beschreiben.
Venn-Diagramme helfen bei der Darstel-
Ergebnisraum Ω
als Menge aller Ergebnisse ωi
eines Zufallsexperiments
Ergebnisraum eines mehrstufigen Zufallsexpe-
riments
Baumdiagramm
Beschränkung auf endliche Ergebnisräume
Vergröberung und Verfeinerung von
.
Zufallsexperimente können auf das Urnenmodell zu-
rückgeführt werden.
Berufsoberschule Ausbildungsrichtung Nichttechnik
Mathematik
Seite 12
lung. Problemstellungen, die in der Um-
gangssprache formuliert sind, können von
den Schülerinnen und Schülern selbststän-
dig in die Ereignissprache und in die for-
male Sprache der Mengenlehre übertragen
werden.
Ereignis als Teilmenge des Ergebnisraums
Venn-Diagramme
Elementarereignis
Sicheres und unmögliches Ereignis
Gegenereignis
Verknüpfung von Ereignissen
Gesetze von de Morgan
Unvereinbarkeit von Ereignissen
Verknüpfung und Unvereinbarkeit auf zwei Ereignisse
beschränken
12.6 Relative Häufigkeit und Wahr-
scheinlichkeit
14 Std.
Mit Hilfe des empirischen Gesetzes der
großen Zahlen kommt man vom Begriff
der relativen Häufigkeit zu dem der Wahr-
scheinlichkeit. Die Gesetze der Wahr-
scheinlichkeitsrechnung werden aus den-
jenigen der relativen Häufigkeit abgeleitet.
Die Schülerinnen und Schüler arbeiten mit
der Vierfeldertafel und erkennen die Be-
deutung des Begriffs „stochastische Un-
abhängigkeit“.
Relative Häufigkeit eines Ereignisses und de-
ren Eigenschaften
Empirisches Gesetz der großen Zahlen
Laplace-Experiment
Laplace-Wahrscheinlichkeit
Rechnen mit Wahrscheinlichkeiten
Wahrscheinlichkeitsverteilung
Satz von Sylvester für zwei Ereignisse
Vierfeldertafel
Stochastische (Un-)Abhängigkeit zweier Er-
eignisse
Computereinsatz
Auf den Begriff „Bedingte Wahrscheinlichkeit“ kann
verzichtet werden.
Die historischen Anfänge der Wahrscheinlichkeitsrech-
nung können hier angesprochen werden.
Wahrscheinlichkeit des Gegenereignisses
Anwendungsbezogene Aufgaben
Eigene Untersuchungen durchführen lassen
Grenzen der Aussagekraft diskutieren
12.7 Berechnung von Wahrscheinlich-
keiten
12 Std.
Ausgehend vom Baumdiagramm erhalten
die Schülerinnen und Schüler Informatio-
nen sowohl über die Mächtigkeit von Er-
eignissen als auch (mit Hilfe der Pfadre-
Baumdiagramm bei mehrstufigen Zufallsexpe-
rimenten
Pfadregeln
Urnenmodell
Berufsoberschule Ausbildungsrichtung Nichttechnik
Mathematik
Seite 13
geln) über Wahrscheinlichkeiten. Als Mo-
dell für viele reale Vorgänge lernen sie die
Bernoulli-Kette kennen.
Allgemeines Zählprinzip
n! und Binomialkoeffizient
Berechnung von Wahrscheinlichkeiten bei
Bernoulli-Ketten
Verwendung eines Tafelwerks
Nur Aufgaben, die mit Baumdiagramm oder allgemei-
nem Zählprinzip zu lösen sind
Die Kombinatorik wird nur noch benötigt, um die For-
mel für den Binomialkoeffizienten herzuleiten.
Auf weitere kombinatorische Formeln und auf das Pro-
dukt von Binomialkoeffizienten wird verzichtet.
Aufgaben mit und ohne Verwendung des Tafelwerks
Verzicht auf die Berechnung der Kettenlänge
12.8 Zufallsgröße und Wahrscheinlich-
keitsverteilung
16 Std.
Die Schülerinnen und Schüler übertragen
den Funktionsbegriff auf die Stochastik.
Sie lernen, Zufallsgröße und Wahrschein-
lichkeitsverteilung als Funktionen darzu-
stellen und auszuwerten. Beim Vergleich
von Wahrscheinlichkeitsverteilungen er-
kennen sie die Notwendigkeit für die Ein-
führung der Maßzahlen Erwartungswert,
Varianz und Standardabweichung. Sie
können Spielangebote vergleichen und
beurteilen. Das Tafelwerk lernen sie als
weiteres Hilfsmittel beim Lösen von Auf-
gaben kennen.
Zufallsgröße
Zufallswert
Wahrscheinlichkeitsverteilung einer Zufalls-
größe
–
in Tabellenform
–
in grafischer Darstellung, Histogramm u. a.
Erwartungswert
Varianz und Standardabweichung
Verschiebungsformel
Binomialverteilte Zufallsgröße und ihre cha-
rakteristische Maßzahlen
Kumulative Verteilungsfunktion der Binomial-
verteilung
Auf den Begriff der Wahrscheinlichkeitsfunktion kann
verzichtet werden.
Im Rahmen von anwendungsbezogenen Aufgaben kön-
nen hier auch Häufigkeitsverteilungen und Begriffe wie
Klassenbildung, Median, Quartil etc. behandelt werden.
„faires“ Spiel
Computereinsatz zum Erstellen und Veranschaulichen
von Binomialverteilungen
Kumulative Verteilungsfunktionen nur bei binomialver-
teilten Zufallsgrößen; keine grafische Darstellung
12.9 Testen von Hypothesen
9 Std.
An Beispielen erkennen die Schülerinnen
Ziel eines Hypothesentests
Der Begriff der repräsentativen Stichprobe sollte exem-
Berufsoberschule Ausbildungsrichtung Nichttechnik
Mathematik
Seite 14
und Schüler die Bedeutung von Testver-
fahren. Sie lernen, mit den Begriffen si-
cher umzugehen, und können Risiken ab-
schätzen und Irrtumswahrscheinlichkeiten
berechnen. Sie erkennen, dass der Aus-
gang eines Tests von der Entscheidungs-
regel abhängt.
Stichprobe
Testgröße
Nullhypothese und Gegenhypothese
Entscheidungsregel
Ablehnungsbereich der Nullhypothese
Fehler 1. und 2. Art
Signifikanzniveau
Einseitiger Signifikanztest bei zugrunde lie-
gender Binomialverteilung
plarisch erläutert werden.
Der Nichtablehnungsbereich wird auch als Annahmebe-
reich bezeichnet.
Auf den Unterschied zwischen Signifikanzniveau und
Irrtumswahrscheinlichkeit hinweisen
Praxisnahe Anwendungen
Keine zweiseitigen Tests
Die Wahrscheinlichkeit für den Fehler 2. Art kann nicht
berechnet werden.
Berufsoberschule Ausbildungsrichtung Nichttechnik
Mathematik
Seite 15
LEHRPLÄNE
MATHEMATIK
Jahrgangsstufe 13
Lerngebiete:
Analysis
13.1 Eigenschaften gebrochen-rationaler Funktionen
12 Std.
13.2 Ableitungsregeln
8 Std.
13.3 Kurvendiskussion gebrochen-rationaler Funktionen
15 Std.
13.4 Kurvendiskussion von Exponential- und Logarithmusfunktionen 15 Std.
13.5 Kurvendiskussion zusammengesetzter Exponential- und
Logarithmusfunktionen
36 Std.
Lineare Algebra und Analytische Geometrie
13.6 Vektoren im IR
2
und IR
3
12 Std.
13.7 Matrizen
9 Std.
13.8 Lineare Unabhängigkeit von Vektoren im IR
2
und IR
3
;
lineare Gleichungssysteme
23 Std.
13.9 Leontief-Modell
12 Std.
13.10 Geometrische Anwendungen im IR
3
23 Std.
165 Std.
LERNINHALTE
HINWEISE ZUM UNTERRICHT
Analysis
13.1 Eigenschaften gebrochen-rationaler
12 Std.
Berufsoberschule Ausbildungsrichtung Nichttechnik
Mathematik
Seite 16
Funktionen
Die Schülerinnen und Schüler lernen die
gebrochen-rationalen Funktionen kennen
und üben sich darin, Eigenschaften solcher
Funktionen zu bestimmen.
Echt und unecht gebrochen-rationale Funktio-
nen
Verhalten der Funktionswerte in der Umge-
bung einer Definitionslücke und für x 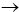 ±
±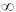
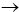 ±
±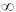
.
Unendlichkeitsstelle und stetig behebbare De-
finitionslücke, stetige Fortsetzung
Polynomdivision mit Rest
Senkrechte, waagrechte und schiefe Asympto-
ten
Eigenschaften der Potenzfunktionen f:
x 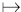 x–n
x–n
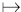 x–n
x–n mit
n
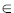
IN ansprechen
Lösen von Bruchgleichungen und Bruchungleichungen
Unendlichkeitsstellen mit und ohne Vorzeichenwechsel
unterscheiden
Auf Schnittpunkte mit Asymptoten eingehen
13.2 Ableitungsregeln
8 Std.
Die Schülerinnen und Schüler lernen den
Begriff der Verkettung kennen, erarbeiten
sich die Ableitungsregeln und wenden
diese zur Ableitung von rationalen Funk-
tionen an.
Produktregel
Quotientenregel
Verkettung von Funktionen und Kettenregel
Ableitung von rationalen Funktionen
Beispiele für Verkettung:

bzw.
f(x) = (3x + 2)4
13.3 Kurvendiskussion gebrochen-
rationaler Funktionen
15 Std.
Die Schülerinnen und Schüler gewinnen
Sicherheit in der Kurvendiskussion gebro-
chen-rationaler Funktionen. Sie üben sich
in der Berechnung einfacher Integrale.
Kurvendiskussion von gebrochen-rationalen
Funktionen
Integrale der Form
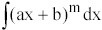
mit
m
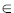
Z \ {–1}
Uneigentliche Integrale 1. Art
Auf die Diskussion von Funktionenscharen wird verzich-
tet.
Erweiterung des Begriffs Flächeninhalt
Berufsoberschule Ausbildungsrichtung Nichttechnik
Mathematik
Seite 17
13.4 Exponential- und Logarithmusfunk-
tionen
15 Std.
13.4.1 Die Schülerinnen und Schüler ler-
nen die Exponential- und Loga-
rithmusfunktionen kennen. Zum
Lösen entsprechender Gleichungen
werden die Potenz- und Logarith-
musgesetze angewendet. Anhand
charakteristischer Anwendungsbei-
spiele entwickeln sie ein Bewusst-
sein für die Bedeutung dieser Funk-
tionen.
Exponentialfunktionen mit Basis a
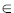
IR
+
\{1}
Eigenschaften der Funktionsgraphen
Exponentielles Wachstum und exponentielle
Abnahme
Logarithmusfunktionen als Umkehrfunktionen
der Exponentialfunktionen
Logarithmusgesetze, Basisumrechnung
Eigenschaften der Funktionsgraphen
Als Anwendungsbeispiele eignen sich: Kapitalmehrung,
radioaktiver Zerfall, Bevölkerungswachstum, Bier-
schaumzerfall etc.
Hier sollen auch Beispiele zum dekadischen Logarithmus
betrachtet werden (pH-Wert, Lautstärkeskala etc.).
Verwendung auch von logarithmischen Skalen
13.4.2 Die Schülerinnen und Schüler ler-
nen die Exponentialfunktion mit
Basis e sowie die natürliche Loga-
rithmusfunktion und deren Ablei-
tungen kennen. Sie erwerben die
Fähigkeit, Integrale zu berechnen,
die mit der Exponentialfunktion
oder der Logarithmusfunktion in
Zusammenhang stehen.
Exponentialfunktion mit Basis e
Ableitung der natürlichen Exponentialfunktion
Logarithmusfunktion mit Basis e
Ableitung der natürlichen Logarithmusfunktion
Bestimmung von 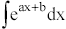
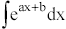
durch Umkehrung
der Kettenregel
Berechnung von Integralen unter Verwendung
von
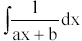
Darstellung von e als Grenzwert von
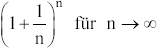
Die Methode, die Ableitung einer Funktion durch die
Ableitung ihrer Umkehrfunktion zu gewinnen, sollte ex-
emplarisch vorgestellt werden.
Beispiele auch der Form:
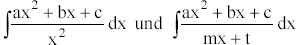
13.5 Kurvendiskussion zusammengesetz-
ter Exponential- und Logarithmus-
funktionen
36 Std.
Berufsoberschule Ausbildungsrichtung Nichttechnik
Mathematik
Seite 18
13.5.1 Die Schülerinnen und Schüler er-
fahren, dass die Regeln von
de L’Hospital geeignet sind, das
Berechnen von Grenzwerten zu er-
leichtern.
Regeln von de L’Hospital
Es genügt, die Regeln plausibel zu machen und sich auf
die Fälle
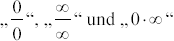
zu beschränken.
13.5.2 Die Schülerinnen und Schüler ler-
nen, ihr erworbenes Wissen zur
Kurvendiskussion auf Funktionen
anzuwenden, die Exponential- und
Logarithmusfunktionen enthalten.
Sie erkennen, dass sich eine breite
Palette von Anwendungen – exakt
oder näherungsweise – mit Hilfe
dieser Funktionen beschreiben lässt
und die Differenzial- und Integral-
rechnung wichtige Hilfsmittel zur
Untersuchung bereitstellt. Sie ver-
suchen selbst Funktionen zu ermit-
teln, die Sachzusammenhänge nä-
herungsweise beschreiben.
Kurvendiskussion von Funktionen, die als Pro-
dukt, Quotient, Summe oder Verkettung von
Exponential-, Logarithmus- und Polynomfunk-
tionen sowie gebrochen-rationalen Funktionen
entstehen
Flächenberechnungen
Anwendungsaufgaben und Modellbildung
Beschränkung auf einfache Funktionstypen
Die mathematischen Begriffe (Steigung, Krümmung,
Extremum, Wendepunkt, Grenzwert etc.) sollten noch-
mals in verschiedenen Sachzusammenhängen illustriert
werden.
Das Aufstellen von Näherungsfunktionen kann beson-
ders bei größeren Datenmengen mit Computerunterstüt-
zung erfolgen.
13.6 Vektoren im IR
2
und IR
3
12 Std.
Die Schülerinnen und Schüler lernen mit
Hilfe der Deutung eines Vektors als
Translation die Darstellung von Vektoren
in einem kartesischen Koordinatensystem
Geometrischer Vektor als Menge aller parallel-
gleichen Pfeile
Repräsentant eines Vektors
Nullvektor, Gegenvektor
Vektorielle Größen aus der Physik dienen zur Verdeutli-
chung
Berufsoberschule Ausbildungsrichtung Nichttechnik
Mathematik
Seite 19
der Ebene oder des Raumes kennen.
Durch die Verkettung von Translationen
wird die Vektoraddition und die S-Multi-
plikation einsichtig.
Die Schülerinnen und Schüler lernen, mit
Hilfe der Addition und S-Multiplikation in
Koordinatenschreibweise mit Vektoren zu
rechnen.
Addition von Vektoren und S-Multiplikation
und deren Rechengesetze
Punkte und Ortsvektoren, Koordinatensysteme,
Koordinaten
Addition und S-Multiplikation in Koordinaten-
schreibweise
Auf die axiomatische Behandlung des Vektorraums wird
verzichtet.
Unterscheidung zwischen Punkten und Vektoren
13.7 Matrizen
9 Std.
Die Schülerinnen und Schüler lernen mit
Hilfe von Matrizen und deren Verknüp-
fungen eine Möglichkeit kennen, Größen
und Beziehungen einfach darzustellen.
Matrix als Zahlenschema
Addition von Matrizen
Multiplikation einer Matrix mit einer reellen
Zahl
Multiplikation einer Matrix mit einem Vektor
Rechengesetze, Einheitsmatrix
Stückliste
Übergangsmatrix
Verflechtungstabelle
13.8 Lineare Unabhängigkeit von Vekto-
ren im IR
2
und IR
3
; lineare Glei-
chungssysteme
23 Std.
Die Schülerinnen und Schüler lernen, dass
die Verbindung von Addition und S-
Multiplikation zur Linearkombination von
Vektoren führt. Der Versuch, einen Vek-
tor als Linearkombination von Vektoren
zu schreiben, führt sie zu einem linearen
Gleichungssystem. Die Schülerinnen und
Linearkombination von Vektoren
Produkt aus einer Matrix und einem Vektor
Gauß-Algorithmus
Lösbarkeit eines linearen Gleichungssystems,
Lineare Abhängigkeit und Unabhängigkeit von
Vektoren
Basis und Dimension eines reellen Vektor-
Deutung der Gleichungen des Systems als Koordinaten-
gleichungen einer Vektorgleichung
Über- und unterbestimmtes System
Kollineare, komplanare Vektoren
Hier keine Berechnung von Teilverhältnissen
Berufsoberschule Ausbildungsrichtung Nichttechnik
Mathematik
Seite 20
Schüler lösen das lineare Gleichungssys-
tem und lernen das Gauß-Eliminations-
verfahren als leistungsfähige Lösungsme-
thode kennen. Die eindeutige Darstellbar-
keit eines Vektors als Linearkombination
führt sie dann zur Definition der linearen
Unabhängigkeit von Vektoren und zu den
Begriffen der Basis und Dimension eines
Vektorraums.
raums
Koordinaten eines Vektors bezüglich einer be-
liebigen Basis
Anwendungsaufgaben zu linearen Gleichungs-
systemen mit höchstens vier Unbekannten
Lineare Gleichungssysteme werden auch zum Aufstellen
von Funktionsgleichungen in der Analysis verwendet.
13.9 Leontief-Modell
12 Std.
Die Schülerinnen und Schüler lernen, die
Beschreibung von wirtschaftlichen Zu-
sammenhängen durch Matrizen in der In-
put-Output-Analyse kennen und lösen ent-
sprechende Anwendungsaufgaben auch
mit dem Gauß-Algorithmus
Input-Output-Analyse, Leontief-Modell
Produktionsvektor 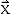 , Konsumvektor
, Konsumvektor 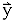
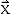 , Konsumvektor
, Konsumvektor 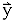
, In-
putmatrix A
(E – A) · 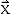 =
= 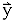
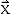 =
= 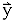
Volkswirtschaftliche und betriebswirtschaftliche An-
wendungen
Anstelle des Begriffs Konsumvektor sind auch die Be-
griffe Marktvektor oder Nachfragevektor gebräuchlich.
13.10 Geometrische Anwendungen im IR
3
23 Std.
Die Schülerinnen und Schüler lernen,
Punkte, Geraden und Ebenen darzustellen
sowie Aussagen über die gegenseitige La-
ge und die Schnittmenge zu machen. Li-
neare Gleichungssysteme lassen sich nun
geometrisch interpretieren und deren Lö-
sung lässt sich deuten. Sie lernen, sich die
gegenseitige räumliche Lage der geomet-
rischen Objekte vorzustellen und in Skiz-
zen darzustellen.
Punktraum
Geradengleichung
Parameterform, Koordinatenform und Achsen-
abschnittsform der Ebenengleichung
Besondere Lagen von Geraden und Ebenen im
Koordinatensystem
Gegenseitige Lage von Punkten, Geraden und
Ebenen
Schnittmengen
Die Koordinatenform der Ebenengleichung kann mit Hil-
fe des Gauß-Algorithmus gewonnen werden.
Schnitt mehrerer Ebenen
Berufsoberschule Ausbildungsrichtung Nichttechnik
Mathematik
Seite 21
ANLAGE
Mitglieder der Lehrplankommission:
Claus Katzer
München
Dieter Pratsch
Augsburg
Michael Storath
Kempten
Werner Maul
ISB, München
Jakob Maurer
ISB, München