|
||||||||||||||||||||||||
 |
 |
|||||||||||||||||||||||
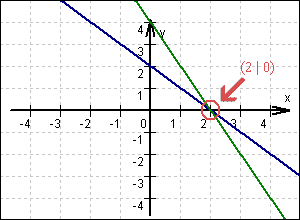
| S ( 2 | 0 ) 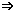 Lösung: x = 2; y = 0 Lösung: x = 2; y = 0 |
 |
|||||||||||||||||||||||
|
||||||||||||||||||||||||
 |
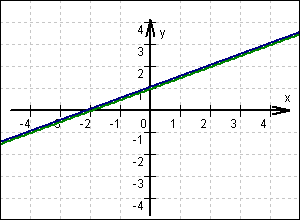 |
|||||||||||||||||||||||
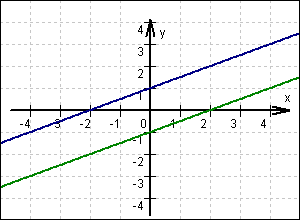
| kein Schnittpunkt 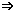 keine Lösung keine Lösung |
S(x | y) mit y = 0,5x + 1 und x 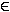 IR IR 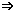 Lösungen: x Lösungen: x 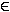 IR; y = 0,5x + 1 IR; y = 0,5x + 1 |
|||||||||||||||||||||||
| (1) |
5x + 5(1 + y) = 3x + 10y
|
Beide Gleichungen in die Standardform bringen | |||
| (2) | 4(x + 3) – 2y = x – 6y + 39 | ||||
| (1) | 2x – 5y = – 5 | ||||
| (2) | 3x + 4y = 27 | ||||
| (1) | 2x – 5y = – 5 | · 3 | Beide Gleichungen mit geeigneten Zahlen multiplizieren, so dass die Faktoren vor x den gleichen Betrag, aber verschiedene Vorzeichen haben. | ||
| (2) | 3x + 4y = 27 | ·(–2) | |||
| (1) | 6x – 15y = – 15 | Die beiden Gleichung addieren. Es entsteht eine Gleichung, in der x nicht mehr auftritt. |
|||
| (2) | – 6x – 8y = – 54 | ||||
| (3) | –23y = – 69 | ||||
| (3) | – 23y = – 69 | :(–23) | Diese Gleichung nach y auflösen. | ||
| y = 3 | |||||
| (1) | 2x – 15 = – 5 | + 15 | Wert für y in die erste Gleichung einsetzen und diese nach x auflösen. | ||
| 2x = 10 | : 2 | ||||
| x = 5 | |||||
| Probe durchführen | |||||
| (1) | 25 + 5·(1 + 3) = 15 + 30 | Zwei wahre Aussagen! | |||
| (2) | 4· (5 + 3) –6 = 5 – 18 + 39 |
| (1) |
a + b = c + 7
|
Als ersten Schritt bringen wir die Gleichungen in die Standardform. | |||
| (2) | 2a – b = 8 – c | ||||
| (3) | 3a + 2b = c + 20 | ||||
| (1) | a + b – c = 7 | ·3 | Nun multiplizieren wir die 1. und die 3. Gleichung mit den geeigneten Zahlen, so dass die Faktoren vor "a" den gleichen Betrag aber entgegengesetzte Vorzeichen haben. | ||
| (2) | 2a – b + c = 8 | ||||
| (3) | 3a + 2b – c = 20 | ·(–1) | |||
| (1) | 3a + 3b – 3c = 21 | Jetzt addieren wir die 1. und 3. Gleichung. Eo entsteht eine neue Gleichung (4), in der a nicht mehr auftritt. | |||
| (3) | –3a – 2b + c = – 20 | ||||
| (4) | b – 2c = 1 | ||||
| (1) | a + b – c = 7 | ·2 | Nun multiplizieren wir die 1. und 2. Gleichung mit den geeigneten Zahlen, so dass die Faktoren vor "a" den gleichen Betrag, aber entgegengesetzte Vorzeichen haben. | ||
| (2) | 2a – b + c = 8 | ·(–1) | |||
| (1) | 2a + 2b – 2c = 14 | Jetzt addieren wir die 1. und 2. Gleichung. Es entsteht eine neue Gleichung (5), in der "a" nicht mehr auftritt. | |||
| (2) | –2a + b – c = –8 | ||||
| (5) | 3b – 3c = 6 | ||||
| (4) | b – 2c = 1 | ||||
| (5) | 3b – 3c = 6 | :(–3) | |||
| (4) | b – 2c = 1 | ||||
| (5) | –b + c = –2 | Jetzt addieren wir die 4. und 5. Gleichung. Es entsteht eine neue Gleichung (6), in der "a" und "b" nicht mehr auftreten. | |||
| (6) | –c = –1 | ||||
| (6) | –c = –1 | · (–1) | |||
| c = 1 | |||||
| Falls mehr als drei Variable vorhanden sind:Mit diesem Verfahren fortfahren , bis in der letzten Gleichung nur noch eine Variable steht. Nach dieser Variable auflösen. | |||||
| (4) | b – 2·1 = 1 | ||||
| oder | Nun setzen wir den Wert für die letzte Variable "c = 1" in die 4. oder 5. Gleichung, die zwei Variablen beinhalten, ein und lösen nach "b" auf. | ||||
| (5) | –b + 1 = –2 | ||||
| b = 3 | |||||
| (1) | a + 3 – 1 = 7 | Als letzten Schritt setzen wir das Ergebnis von Gleichung (6) "c = 1" und das Ergebnis von Gleichung (4) oder (5) "b = 3" in die 1. Gleichung ein und lösen nach "a" auf. | |||
| a = 5 | |||||
| a = 5 | |||||
| b = 3 | |||||
| c = 1 | |||||
| Das LGS hat keine Lösung: | Das LGS hat unendlich viele Lösungen: | Das LGS hat genau eine Lösung: | ||||||||||||
| (1) | 2x – 3y + 2z = 1 | (1) | 2x – 3y + 2z = 1 | (1) | 2x + 3y + 4z = 20 | |||||||||
| (2) | –4x + 6y – 4z = –2 | (2) | –4x + 6y – 4z = –2 | (2) | –2x – 2y + 3z = 3 | |||||||||
| (3) | x – 1,5y + z = 1 | ·( –2) | (3) | x – 1,5y + z = 0,5 | ·( –2) | (3) | –x – 3y + 4z = 5 | |||||||
| (1) | 2x – 3y + 2z = 1 | (1) | 2x – 3y + 2z = 1 | (1) | 2x + 3y + 4z = 20 | |||||||||
| (2) | –4x + 6y – 4z = –2 | (2) | –4x + 6y – 4z = –2 | (3) | –x – 3y + 4z = 5 | |||||||||
| (3) | –2x + 3y – 2z = –2 | (3) | –2x + 3y – 2z =–1 | (4) | x + 8z = 25 | |||||||||
| (1) | 2x – 3y + 2z = 1 | (1) | 2x – 3y + 2z = 1 | (2) | –2x – 2y + 3z = 3 | ·3 | ||||||||
| (3) | –2x + 3y – 2z = –2 | (3) | –2x + 3y – 2z = –1 | (3) | –x – 3y + 4z = 5 | ·(–2) | ||||||||
| (4) | 0 + 0 + 0 = –1 (falsche Aussage) |
(4) | 0 + 0 + 0 = 0 (wahre Aussage) |
|||||||||||
| Die falsche Aussage |
Das LGS ist also für alle Zahlentripel erfüllt, die die beiden ersten Gleichungen erfüllen. | (2) | –6x – 6y + 9z = 9 | |||||||||||
| (3) | 2x + 6y – 8z = –10 | |||||||||||||
| (5) | –4x + z = –1 | : 4 | ||||||||||||
| (1) | 2x – 3y + 2z = 1 | (5) | –x + 0,25z = –0,25 | |||||||||||
| (2) | –4x + 6y – 4z = –2 | : 2 | (4) | x + 8z = 25 | ||||||||||
| (6) | 8,,25z = 24,75 | |||||||||||||
| (1) | 2x – 3y + 2z = 1 | |||||||||||||
| (2) | –2x + 3y – 2z = –1 | z = 3 | ||||||||||||
| (5) | 0 + 0 + 0 = 0 (wahre Aussage) |
y = 2 | ||||||||||||
| x = 1 | ||||||||||||||
Die Lösungen sind die Tripel 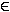 IR IR |
||||||||||||||
| (1) | 3x – 4y = 22 | Gegeben sind zwei Gleichungen; eine von
ihnen muss erst in die richtige Form, und zwar |
|||
| (2) | 9x + 3y = 6 | ||||
| (1) | 3x – 4y = 22 | In diesem Fall lösen wir die 2.Gleichung
nach y auf und bringen sie in die Form |
|||
| (2) | y = 2 – 3x | ||||
| (1) | 3x – 4·(2 – 3x) = 22 | Nun setzen wir den Term „2 – 3x“ von der 2. Gleichung für y in die 1. Gleichung ein. | |||
| (1) | 3x – 8 + 12x = 22 | Nun lösen wir die 1. Gleichung nach x auf. | |||
| (1) | 15x = 30 | ||||
| (1) | x = 2 | Nun setzen wir den x-Wert „2“ in die 2. Gleichung für x ein, um den y-Wert zu berechnen. | |||
| (1) | x = 2 | Nun die 2. Gleichung nach y auflösen. | |||
| (2) | y = 2 – 3 · 2 | ||||
| (1) | x = 2 | ||||
| (2) | y = – 4 | ||||
| (1) | 3 · 2 – 4 (–4) = 22 | Als letzten Schritt setzen wir die Ergebnisse der beiden Gleichungen in die Ausgangsgleichungen ein um zu prüfen, ob das Ergebnis richtig ist. | |||
| (2) | 9 · 2 + 3 (–4) = 6 | ||||
| (1) | 22 = 22 | Die Gleichungen ergeben wahre Aussagen. Deshalb ist das Ergebnis richtig. | |||
| (2) | 6 = 6 |
| a) | b) | c) | ||||||||||
|
0,5x + 0,75y = 5
|
y – x = 3
|
y = 1,5x + 2 | ||||||||||
| 2x + 3y = 12 | 2y = 2x + 6 | y + 1,25x + 3 = 0 | ||||||||||
| 0,5x + 0,75y = 5 | y – x = 3 | 1,5x + 2 + 1,25x + 3 = 0 | ||||||||||
| x = 6 – 1,5y | y = x + 3 | 2,75x = –5 | ||||||||||
| 0,5·(6 – 1,5y) + 0,75y = 5 | x + 3 – x = 3 | x = –1,818 | ||||||||||
| 3 – 0,75y + 0,75y = 5 | 3 = 3 wahre Aussage |
y = –2,727 + 2 | ||||||||||
| 3 = 5 falsche Aussage |
Alle Zahlenpaare
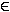 IR IR |
y = –0,727 |
| Das Gleichungssystem hat keine Lösung. | Das Gleichungssystem hat unendlich viele Lösungen. | Das Gleichungssystem hat genau eine Lösung. |
| (1) | a + b = c + 7 | Als ersten Schritt lösen wir z. B. die 1. Gleichung nach c auf. | |||
| (2) | 2a – b = 8 – c | ||||
| (3) | 3a + 2b = c + 20 | ||||
| (1) | c = a + b – 7 | Nun setzen wir den berechneten Term von c in die 2. und 3. Gleichung ein. | |||
| (2) | 2a – b = 8 – (a + b – 7) | Jetzt werden beide Gleichungen vereinfacht. | |||
| (3) | 3a + 2b = a + b – 7 + 20 | ||||
| (2) | 3a = 15 | Normalerweise müssten wir zunächst wieder eine Variable durch die andere ausdrücken. Hier können wir jedoch gleich a = 5 in Gleichung (3) einsetzen. | |||
| (3) | 2a + b = 13 | ||||
| (2) | a = 5 | Wir lösen nach b auf. | |||
| (3) | 2·5 + b = 13 | ||||
| (3) | b = 3 | Die Werte für a und b setzen wir in Gleichung (1) ein. | |||
| (1) | c = 5 + 3 – 7 | Wir rechnen c aus. | |||
| (1) | c = 1 |
| (1) |
–3x + y = 10
|
Als erstes stellt man beide Gleichungen als Funktionsgleichung der Form y = f(x) dar.. | ||||
| (2) | 2x + y = 5 | |||||
| (1) | y = 3x + 10 | Nun setzt man die Funktionsterme, das
heißt die rechten Seiten der beiden Gleichungen, gleich. |
||||
| (2) | y = – 2x + 5 | |||||
| (3) | 3x + 10 = – 2x + 5 | +2x | Nun löst man die erhaltene Gleichung mit einer Variablen nach dieser Variablen, also hier nach x auf. | |||
| (3) | 5x + 10 = 5 | –10 | ||||
| (3) | 5x = – 5 | : 5 | ||||
| (3) | x = – 1 | Nun setzt man den x–Wert (– 1) in eine der obigen Gleichungen ein. | ||||
| (1) | y = 3(– 1) + 10 | Nun berechnet man y. | ||||
| (1) | y = – 3 + 10 |
|||||
| (1) | y = 7 | Als letzten Schritt führt man die Probe aus. | ||||
| (1) | –3(–1) + 7 = 10 | |
||||
| (2) | 2(–1) + 7 = 5 | |||||
| (1) | 10 = 10 | Die Probe zeigt die Richtigkeit der Lösung, deshalb ist das Zahlenpaar (–1 | 7) die Lösung des linearen Gleichungssystems. | ||||
| (2) | 5 = 5 | |||||