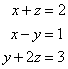Vorkurs

2. Schulaufgabe aus der Mathematik

01.07.08

1.

Eine Parabel besitzt die Nullstellen x₁ = -1,5 und x₂ = 2,5. Außerdem schneidet sie die Gerade y = 2x bei x = -1,25.
Geben Sie eine mögliche Funktionsgleichung der Parabel an.

4 P

2.

Geben Sie Informationen an, die Sie an den folgenden quadratischen Funktionsgleichungen ablesen können, ohne Rechnungen durchzuführen.
a)  
b)
c)

6 P

3.

Gegeben ist die Parabelgleichung  sowie die parameterabhängige Geradengleichung mit .
a) Bestimmen Sie den Parameter a so, dass die Gerade g_a eine Tangente der Parabel ist
    und geben Sie die Koordinaten des Berührpunktes an.        
b) Zeichnen Sie die Parabel p und die Gerade g_-1,5 (das heißt: a = -1,5) in ein
    geeignetes Koordinatensystem ein.

6 P

5 P

4.

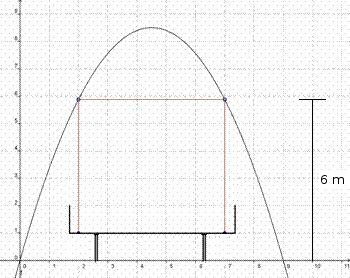
Der parabelförmige Querschnitt eines Eisenbahntunnels lässt sich durch die Funktionsgleichung  darstellen.
Die Lage des Koordinatensystems können Sie aus der Skizze entnehmen.



a) Geben Sie an, wie hoch der Tunnel  an seiner höchsten Stelle ist und bestimmen
    Sie die größte Breite des Tunnels.                                      
b) Ein Zug muss einen übergroßen Container durch den Tunnel transportieren.
    Wie breit darf der Container höchstens sein, wenn er bei einer Gesamthöhe
    (incl. Waggon) von 6 m gerade noch durch den Tunnel passen soll?

4 P

5 P

5.

Lösen Sie das folgende Gleichungssystem:
                                                                             

5 P

Viel Erfolg bei der Bearbeitung !