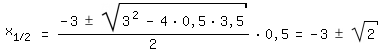
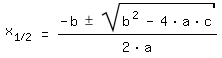
Für
Zwei Teilflächen ergänzen sich zu einem Quadrat
| 1. | |||
| a) | sehr schlanke, nach oben geöffnete Parabel in Scheitelform; Scheitel bei S(2/9); keine Nullstellen | Scheitelform: |
|
| a ist viel größer als 1, dadurch ist die Parabel sehr schlank; a > 0 |
|||
| b) | nach unten geöffnete breite Parabel in der Nullstellen- bzw. Linearfaktorform; Nullstellen bei |
Linearfaktorform: |
|
| c) | steigende Gerade, y-Achsenabschnitt bei -5 | g(x) = m x + t, wobei t den y-Achsenabschnitt beschreibt; m > 0 |
|
| 2. | |||
| 2.1 | Scheitelpunkt: |
Scheitelform: |
|
| in p(x) eingesetzt | |||
| in Scheitelform: |
|||
| 2.2 | |||
| Diskriminante: |
|||
| 2 Nullstellen, da Diskriminante positiv | |||
| 3. | |||
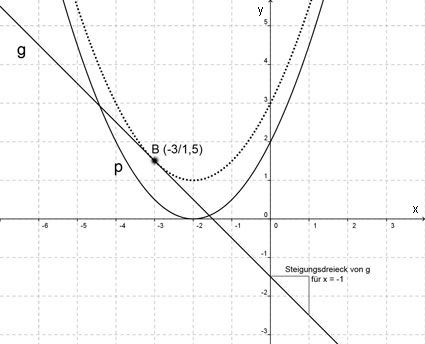
| 3.1 |  |
||
| Scheitel: |
|||
| in p(x) eingesetzt | |||
| Wertetabelle: |
|||
| Funktionen gleichsetzen, um gemeinsame Punkte zu ermitteln! | |||
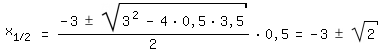 |
Mitternachtsformel: 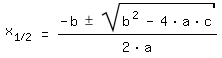 |
||
Für |
|||
| 3.2 | Funktionen gleichgesetzten | ||
| die Diskriminante 0 setzen! | |||
| p(-3)=1,5 | |||
| 4. | |||
| 4.1 | |||
| 4.2 | |||
| bei einer nach unten geöffneten Parabel ist der Scheitelpunkt der höchste Punkt. | |||
| 5. | Zwei Teilflächen ergänzen sich zu einem Quadrat |
der markierte Bereich nimmt genau die Hälfte der gesamten Fläche ein, und das sind 2 mal das Quadrat a². | |
| die Bögen passen genau zu einem Kreis zusammen. | |||