| a) | b) | c) | |||||||||||||
| (1) | 2x – 2y – 6 = 0 | (1) | 5x – 3y = –4 | (1) | 9x + 208y – 15 = 0 | ||||||||||
| (2) | x + 2y = 0 | (2) | 12x + 3y = –3 | (2) | –9x + 72y – 55 = 0 | ||||||||||
| (1) | 2x – 2y – 6 = 0 | (1) | 5x – 3y = –4 | (1) | 9x + 208y – 15 = 0 | ||||||||||
| (2) | x + 2y = 0 | (2) | 12x + 3y = –3 | (2) | –9x + 72y – 55 = 0 | ||||||||||
| (3) | 3x – 6 = 0 | +6 | (3) | 17x = –7 | (3) | 280y – 70 = 0 | +70 | ||||||||
| (3) | 3x = 6 | :3 | (3) | 17x = –7 | :17 | (3) | 280y = 70 | :280 | |||||||
| x = 2 | x = 0,412 | y = 0,25 | |||||||||||||
| x einsetzen in (1) | x einsetzen in (1) | y einsetzen in (2) | |||||||||||||
| (1) | 2·2 – 2y – 6 = 0 | +2 | (1) | 5·(–0,412) – 3y = –4 | (2) | –9x + 72·0,25 –55 = 0 | |||||||||
| –2y = 2 | –2,058 – 3y = –4 | +2,058 | –9x – 37 = 0 | +37 | |||||||||||
| y = –1 | –3y = –1,942 | :(–3) | –9x = 37 | ||||||||||||
| y = 0,647 | x = –4,111 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a) | b) | c) | |||||||||||||
| (1) | 2x + 2y = –16 | (1) | 7y – 3x = 6 | (1) | x = 3y – 4 | ||||||||||
| (2) | 2x – 2y = 4 | (2) | 3x + 2y = 3 | –3x | (2) | 3x – 5y = –4 | |||||||||
| (1) | 2x + 2y = –16 | (1) | 7y – 3x = 6 | (2) | 3(3y – 4) – 5y = –4 | ||||||||||
| (2) | 2x = 2y + 4 | :2 | (2) | 2y = –3x + 3 | :2 | 9y – 12 – 5y = –4 | +12 | ||||||||
| 4y = 8 | :4 | ||||||||||||||
| (1) | 2x + 2y = –16 | (1) | 7y – 3x = 6 | y = 2 | |||||||||||
| (2) | x = y + 2 | (2) | y = –1,5x + 1,5 | x =2 | |||||||||||
| (1) | 2·(y + 2) +2y = –16 | (1) | 7·(–1,5x + 1,5) –3x = 6 | ||||||||||||
| 2y + 4 + 2y = –16 | –10,5x + 10,5 – 3x = 6 | ||||||||||||||
| 4y + 4 = –16 | –4 | –13,5x + 10,5 = 6 | –10,5 | ||||||||||||
| 4y = –20 | –13,5x = –4,5 | ||||||||||||||
| y = –5 | x =1/3 | ||||||||||||||
| x = –3 | y = 1 | ||||||||||||||
| d) | e) | f) | |||||||||||||
| (1) | 0,5x + 2y – 5 = 0 | (1) | y = 1,5x + 2 | (1) | y = 3,57x – 1,11 | ||||||||||
| (2) | 0,25x – 1,5y – 2 = 0 | +1,5y | (2) | y + 1,25x + 3 = 0 | (2) | y = 1,35x + 3,55 | –y | ||||||||
| (1) | 0,5x + 2y – 5 = 0 | (2) | 1,5x + 2 + 1,25x + 3 = 0 | –5 | (1) | y = 3,57x – 1,11 | |||||||||
| (2) | 0,25x = 1,5y + 2 | ·4 | 2,75x = –5 | :2,75 | (2) | 0 = 1,35x + 3,55 –y | |||||||||
| x = –1,818 | |||||||||||||||
| (1) | 0,5x + 2y – 5 = 0 | y = –0,727 | (2) | 0 = 1,35x + 3,55 – (3,57x – 1,11) | –4,66 | ||||||||||
| (2) | x = 6y + 8 | –4,66 = –2,22x | |||||||||||||
| x = 2,1 | |||||||||||||||
| (1) | 0,5(6y + 8)+ 2y – 5 = 0 | y = 6,38 | |||||||||||||
| 3y + 4 + 2y –5 = 0 | +1 | ||||||||||||||
| 5y = 1 | :5 | ||||||||||||||
| y = 0,2 | |||||||||||||||
| x = 9,2 | |||||||||||||||
| a) | b) | c) | ||||||||||||
| (1) | 2x + 2y – 2z = 14 | 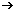 z z |
(1) | 2x + y – z = 7 | 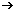 z z |
(1) | 3x – y + 4z = 24 | 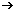 y y |
||||||
| (2) | 2x – y + z = 8 | (2) | x – 3y – 2z = –3 | (2) | x – y + z = 8 | |||||||||
| (3) | 3x + 2y – z = 20 | (3) | 5x + 3y + z = 2 | (3) | 6x – 4y + 5z = 40 | |||||||||
| (1) | z = x + y – 7 | (1) | z = 2x + y – 7 | (1) | y = 3x + 4z – 24 | |||||||||
| z einsetzen in (2) und (3) | z einsetzen in (2) und (3) | y einsetzen in (2) und (3) | ||||||||||||
| (4) | 2x – y + x + y – 7 = 8 | (4) | x – 3y – 2(2x + y – 7) = –3 | (4) | x – (3x + 4z – 24) + z = 8 | |||||||||
| (5) | 3x + 2y – (x + y – 7) = 20 | (5) | 5x + 3y + 2x + y – 7 = 2 | (5) | 6x – 4(3x + 4z – 24) + 5z = 40 | |||||||||
| (4) und (5) vereinfachen | (4) und (5) vereinfachen | (4) und (5) vereinfachen | ||||||||||||
| (4) | 3x = 15 | :3 | (4) | –3x – 5y = –17 | 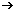 y y |
(4) | –2x – 3z = –16 | 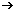 x x |
||||||
| (5) | 2x + y = 13 | (5) | 7x + 4y = 9 | (5) | –6x – 11z = –56 | |||||||||
| (4) | x = 5 | (4) | y = –0,6x + 3,4 | (4) | x = –1,5z + 8 | |||||||||
| x einsetzen in (5) | y einsetzen in (5) | x einsetzen in (5) | ||||||||||||
| 2·5 + y = 13 | 7x + 4(–0,6x + 3,4) = 9 | –6(–1,5z + 8) – 11z = –56 | ||||||||||||
| vereinfachen | vereinfachen | vereinfachen | ||||||||||||
| y = 3 | 4,6x = –4,6 | :4,6 | –2z = –8 | :(–2) | ||||||||||
| x = –1 | z = 4 | |||||||||||||
| x einsetzen in (4) | z einsetzen in (4) | |||||||||||||
| (4) | y = –0,6·(–1) + 3,4 | (4) | x = –1,5·4 + 8 | |||||||||||
| y = 4 | x = 2 | |||||||||||||
| x, y einsetzen in (1) | x, y einsetzen in (1) | x, z einsetzen in (1) | ||||||||||||
| (1) | z = 5 + 3 – 7 | (1) | z = 2·(–1) + 4 – 7 | (1) | y = 3·2 + 4·4 – 24 | |||||||||
| z = 1 | z = –5 | y = –2 | ||||||||||||
| (1) | c = a + b – 7 | (1) = (2) sowie (1) = (3) setzen | |||
| (2) | c = 8 – b – a | ||||
| (3) | c = 3a + 2b – 20 | ||||
| (4) | a + b – 7 = 8 – b – a | nach a auflösen | |||
| (5) | a + b – 7 = 3a + 2b – 20 | ||||
| (4) | 2a = –2b + 15 | :2 | |||
| (5) | –2a = b – 13 | :(–2) | |||
| (4) | a = –b + 7,5 | (4) und (5) gleichsetzen | |||
| (5) | a = –0,5b + 6,5 | ||||
| –b + 7,5 = –0,5b + 6,5 | nach b auflösen | ||||
| –0,5b = –1 | ·(–2) | ||||
| b = 2 | b in (4) einsetzen | ||||
| (4) | a = –2 + 7,5 | ||||
| a = 5,5 | a und b in (1) einsetzen | ||||
| (1) | c = 5,5 + 2 – 7 | nach c auflösen | |||
| c = 0,5 | |||||
| Masse einer blauen Kugel: b Masse einer grünen Kugel: g Masse einer roten Kugel: r. Dann gelten folgende Gleichungen: |
|||||
| (1) | 5g + 2b = 3r | Alle Unbekannten geordnet auf eine Seite stellen | |||
| (2) | 3g = r + 2b | ||||
| (3) | g + 2b = 1 | ||||
| (1) | 2b + 5g – 3r = 0 | ||||
| (2) | –2b + 3g – r = 0 | ·(–3) | |||
| (3) | 2b + g = 1 | ||||
| (1) | 2b + 5g – 3r = 0 | ||||
| (2) | 6b – 9g + 3r = 0 | ||||
| (4) | 8b – 4g = 0 | :4 | |||
| (4) | 2b – g = 0 | ||||
| (3) | 2b + g = 1 | ||||
| (5) | 4b = 1 | :4 | |||
| b = 0,25 | b in (3) | ||||
| 2·0,25 + g = 1 | –0,5 | nach g auflösen | |||
| g = 0,5 | b, g in (2) | ||||
| –2·0,25 + 3·0,5 – r = 0 | |||||
| r = 1 | |||||
| Die blaue Kugel wiegt 250 g, die grüne 500 g und die rote 1 kg. | |||||
| Anzahl der Nägel: n Anzahl der Schrauben: s Anzahl der Muttern: m. Dann gelten folgende Gleichungen: |
|||||
| (1) | m = s | In (2) und (3) m durch s ersetzen | |||
| (2) | n + s + m = 100 | ||||
| (3) | 25n + 20s + 5m = 1500 | ||||
| (2) | n + 2s = 100 | ||||
| (3) | 25n + 25s = 1500 | :(–25) | |||
| (2) | n + 2s = 100 | ||||
| (3) | –n – s = –60 | ||||
| s = 40 | s in (1) und (2) | ||||
| m = 40 | |||||
| (2) | n + 2·40 = 100 | ||||
| n = 20 | |||||
| Die Packung enthält 20 Nägel, 40 Schrauben und 40 Muttern. | |||||
| Anzahl der Nägel: n Anzahl der Schrauben: s Anzahl der Muttern: m. Dann gelten folgende Gleichungen: |
|||||
| (1) | m = s | In (2) und (3) m durch s ersetzen | |||
| (2) | n + s + m = 100 | ||||
| (3) | 15n + 20s + 10m = 1500 | ||||
| (2) | n + 2s = 100 | ||||
| (3) | 15n + 30s = 1500 | :(–15) | |||
| (2) | n + 2s = 100 | ||||
| (3) | –n – 2s = –100 | ||||
| 0 = 0 | Wahre Aussage! | ||||
 Die Zusammensetzung der Packung ist beliebig.
Die Zusammensetzung der Packung ist beliebig.
Erläuterung: In diesem Beispiel wiegen zwei Nägel genau so viel wie eine Schraube und eine Mutter zusammen, nämlich 30 g. Werden also 2 Nägel durch eine Schraube und eine Mutter ersetzt (oder umgekehrt), so ändert sich weder die Anzahl noch die Masse aller Teile, so dass daher jede Zusammenstellung der Packung (mit 100 Teilen und gleicher Schrauben- und Mutternanzahl) die Gesamtmasse von 1,5 kg aufweist.
| Atommasse des Elementes X: x Atommasse des Elementes Y: y Atommasse des Elementes Z: z Dann gelten folgende Gleichungen: |
|||||
| (1) | 3x + y + z = 33 | ||||
| (2) | x + y + 3z = 63 | ·(–1) | |||
| (3) | 4x + 2y + 3z = 80 | ||||
| (1) | 3x + y + z = 33 | ||||
| (2) | –x – y – 3z = –63 | ·2 | |||
| (4) | 2x – 2z = –30 | ||||
| (2) | –2x – 2y – 6z = –126 | ||||
| (3) | 4x + 2y + 3z = 80 | ||||
| (5) | 2x – 3z = –46 | ·(–1) | |||
| (4) | 2x – 2z = –30 | ||||
| (5) | –2x + 3z = 46 | ||||
| z = 16 | z in (4) | ||||
| (4) | 2x – 2·16 = –30 | ||||
| x = 1 | x, z in (1) | ||||
| (1) | 3·1 + y + 16 = 33 | ||||
| y = 14 | |||||
Y hat die Atommasse 14 u. Es handelt sich um N (Stickstoff).
Z hat die Atommasse 16 u. Es handelt sich um O (Sauerstoff).
Hinweis: Es handelt sich um die Verbindungen H3NO = H2NOH (Hydroxilamin), HNO3 (Salpetersäure) und H4N2O3 = NH4NO3 (Ammoniumnitrat).