
Funktionsgleichung
In der Praxis beschreibt eine lineare Funktion den Zusammenhang zweier Größen (in der Mathematik mit x und y bezeichnet), wobei die Größe y in Abhängigkeit von x gleichmäßig zu- bzw abnimmt.
|
Größe y = Wachstumsrate m mal Anzahl der Einheiten x + Startwert t |
 |
Gleichung: y = mx + t
Der Graph der Funktion ist eine Gerade
y = Wert der Größe in Abhängigkeit von x
m = Steigung der Geraden
t = legt Schnittpunkt mit y- Achse fest
(x/y)= Wertepaare die den "x- und y- Wert" eines Punktes der Geraden darstellen
Beispiel: Positive Steigung:
Geraden mit der Gleichung ![]() und
und ![]()
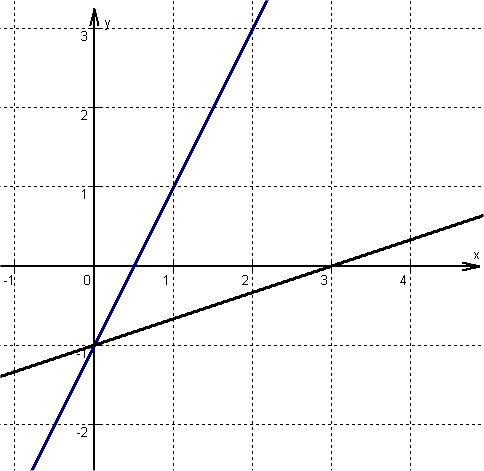 |
Die Geraden verlaufen in x-Richtung steigend!
|
Beispiel Negative Steigung:
Geraden mit der Gleichung ![]() und
und ![]()
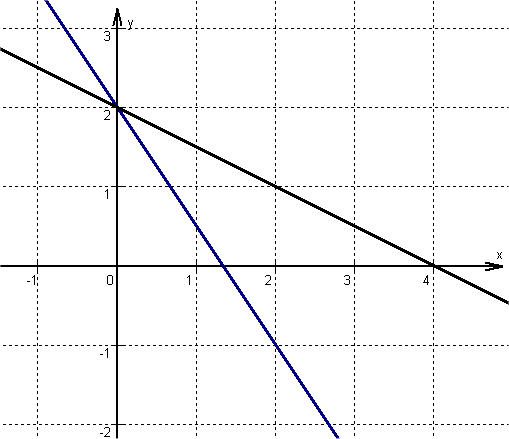 |
Die Geraden verlaufen in x-Richtung fallend. |
Sonderfall:
Ist die Steigung m=0, also die Gleichung der Geraden y = t , so handelt es sich um eine waagrechte Gerade.
Beispiel:
y = 3 ist die Gleichung einer Geraden, die parallel zur x-Achse verläuft
und deren Punkte alle den y-Wert 3 besitzen.
Beispiel Steigungsdreieck:
| Gerade |
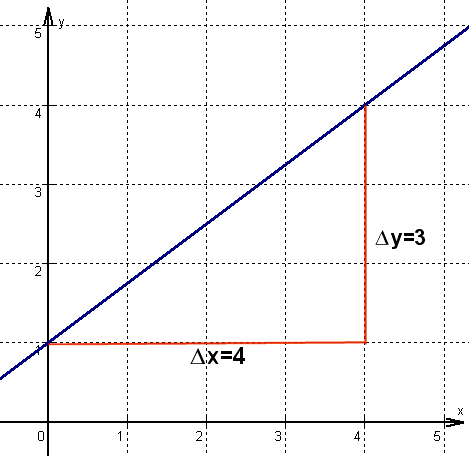 |
Mit dem Punkt (0/t) und dem Steigungsdreieck (4 nach rechts und 3 nach oben)können sehr schnell weitere Punkte für Gf eingezeichnet werden und damit die zugehörige Gerade. Merke: Das Steigungsdreieck kann in jedem Punkt einer Geraden gezeichnet werden!! |
Punkte auf der Geraden:
Ein Punkt P(x/y) liegt auf der Geraden, wenn die Koordinaten des Punktes in die Geradengleichung eingesetzt diese erfüllen. Ergibt sich dagegen eine falsche Aussage, so liegt der Punkt nicht auf der Geraden
Beispiel:
Gegeben ist die Gerade g: y = -2x + 3
a) Liegen die Punkte A(5/-7) und B(10/-14) auf der Geraden?
b) Ergänzen Sie die Koordinaten der Punkte C(-5/?) und D(?/25) so, dass
sie auf der Geraden liegen.
Lösung:
a1) A eingesetzt in g: -7 = -2*5 + 3 ist eine richtige Aussage, also liegt A
auf g.
a2) B eingesetzt in g: -14 = -2*10 + 3 ist falsch, also liegt B nicht auf g.
b1) y = -2*(-5) + 3 = 13 , also heißt der Punkt C(-5/13).
b2) 25 = -2x + 3 , also 22 = -2x und damit x = -11 , der Punkt ist D(-11/25).