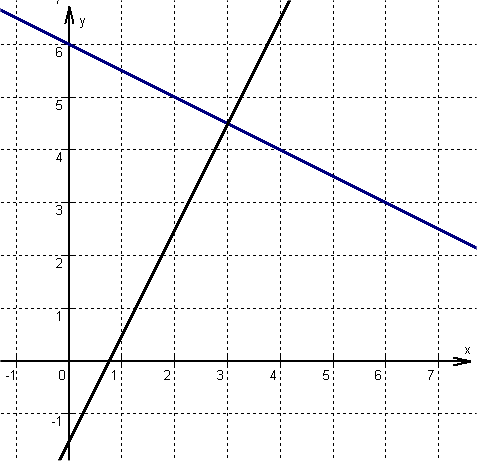schneidet die y-Achse im Punkt T(0/4).Schnittpunkt mit der y-Achse
Dieser wird durch den Wert von t festgelegt: t ist der y-Wert des Schnittpunktes mit der y-Achse. der x-Wert des Schnittpunktes ist immer Null.
Beispiel:
Die Gerade
schneidet die y-Achse im Punkt T(0/4).
Schnittpunkt mit der x-Achse
Der y-Wert dieses Schnittpunktes ist immer Null! Den x-Wert erhält man, indem der y-Wert in der Funktionsgleichung 0 gesetzt wird:
Beispiel:
Gerade mit der Gleichung :
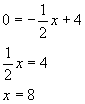
Der Schnittpunkt mit der x-Achse
ist N(8/0).
Der x-Wert alleine wird auch als Nullstelle x=8 bezeichnet.
Schnittpunkt zweier Geraden
Berechnung des x – Wertes:
durch Gleichsetzten der Funktionsterme.
Da die y- Werte beider Funktionen im Schnittpunkt gleich sind, verbindet man den ersten Term mit dem zweiten Term durch ein "Gleichheitszeichen" (=).
Beispiel 1:
| erster
Term: g1: |
zweiter
Term: g2:  |
|
|
|
der x - Wert ist 8
Berechnung des y - Wertes
Zur Berechnung des y - Wertes den x - Wert in einen der beiden Terme einsetzen.
Beispiel: Term eins g1:
y = 
= 0
Der Schnittpunkt ist S(8/0) - siehe Graph:
Beispiel 2:
Gegeben ist die Gerade g:
und die Gerade f:
Zeichnen sie die beiden Geraden und bestimmen sie rechnerisch ihren Schnittpunkt.
Rechnerische Lösung:
die beiden Geraden gleichsetzen
Den x - Wert in eine der beiden Geraden einsetzen:
Der gesuchte Punkt ist S(3/4,5)
