Der Volksmund sagt: „Wenn der Verstand kommt, müssen die Haare weichen.“ Wenn sich diese Volksweisheit auch zunächst nur auf das vorgerückte Mannesalter bezieht, könnte man daraus auch einen anderen Schluss ziehen: „Der Anteil der Männer, die unter Haarausfall leiden (Ereignis H), ist unter Akademikern (Ereignis A) deutlich höher als in der männlichen Gesamtbevölkerung.“ In der Terminologie der Stochastik würde man dann sagen, dass die Ereignisse H und A sich gegenseitig beeinflussen, also „stochastisch abhängig“ wären. Niemand, schon gar kein Akademiker, wird ernsthaft an diesen Zusammenhang glauben, sondern vielmehr davon ausgehen, dass der Anteil der Männer mit Haarausfall unter Akademikern derselbe ist wie in der gesamten männlichen Bevölkerung, dass also die Ereignisse H und A „stochastisch unabhängig“ sind.

Wie kann man nun eine solche Fragestellung stochastisch überprüfen? Hat der Bildungsgrad keinen Einfluss auf die Haarfülle, so kann man sagen, dass das Verhältnis der unter Haarausfall leidenden Akademiker (AH) zur Anzahl aller Akademiker (A) dasselbe ist wie das Verhältnis der insgesamt unter Haarausfall leidenden Männer (H) zur gesamten männlichen Bevölkerung (Ω), also:

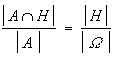Nach Umwandlung der absoluten in die relativen Häufigkeiten ergibt sich dann:

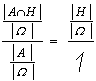Interpretiert man nun die relativen Häufigkeiten als Wahrscheinlichkeiten, so folgt:

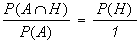Nach Multiplikation der Gleichung mit P(A) lautet die Gleichung:

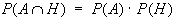Damit haben wir die zentrale Formel für stochastisch unabhängige Ereignisse gefunden:

Zwei Ereignisse  A  und  B  mit  P(A)> 0  und  P(B)> 0  heißen genau dann (stochastisch) unabhängig, wenn gilt: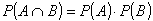 In diesem Fall wird die Wahrscheinlichkeit des einen Ereignisses durch das Eintreten des anderen Ereignisses nicht verändert.

Stochastisch voneinander unabhängig sind dann auch die Ereignisse A und 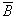, 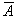und B sowie 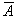und .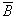
(Zur Wiederholung: Venn-Diagramme)

Hinweis: Diese Formel für die stoch. Unabhängigkeit von Ereignissen haben wir schon bei den Baumdiagrammen benutzt. Sie ist nämlich der Gegenstand der 1. Pfadregel. Ein korrekt erstelltes Baumdiagramm enthält nämlich längs eines Pfades lauter stochastisch unabhängige Ereignisse.

Die scheinbar einfache und einsichtige Definition stochastischer Unabhängigkeit bereitet in der Anwendung mitunter Schwierigkeiten. Das hat seine Ursache unter anderem darin, dass dieser Begriff der Stochastik bewusst oder unbewusst mit anderen Vorstellungen (z.B. aus dem täglichen Sprachgebrauch) verbunden wird, die nicht mit der Definition zu vereinbaren sind:

Die Unabhängigkeit von Ereignissen darf nicht mit der Unvereinbarkeit von Ereignissen verwechselt werden.
Die Unvereinbarkeit zweier Ereignisse A, B wird definiert als A 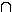B = {}, d.h. Unvereinbarkeit ist eine Eigenschaft der Ereignisse, die ihre Wahrscheinlichkeiten außer Acht lässt. Unabhängigkeit von zwei Ereignissen kann aber nicht bestimmt werden ohne die Wahrscheinlichkeiten dieser Ereignisse. Es kommt hinzu, dass die gemeinsame Vorsilbe "un" manchen zu der Vorstellung verleitet, unvereinbare Ereignisse müssten unabhängig sein.
Das ist falsch, denn es gilt das Gegenteil:

• Sind zwei Ereignisse A und B mit P(A) > 0 unvereinbar, so sind sie nicht voneinander unabhängig.

Häufig steht man in der Praxis vor der Situation, die Unabhängigkeit zweier Ereignisse auf der Grundlage einer Analyse der entsprechenden Sachzusammenhänge anzunehmen. Das ermöglicht es einerseits, die Definitionsgleichung bzw. den Multiplikationssatz als Berechnungsformel zu nutzen. Andererseits hat eine fälschlicherweise angenommene Unabhängigkeit oft gravierende Auswirkungen in Gestalt einen systematischen Fehlers.