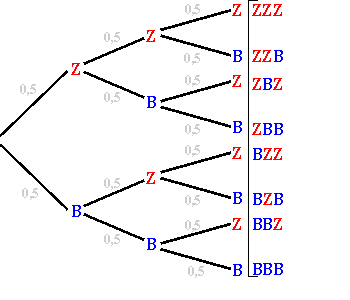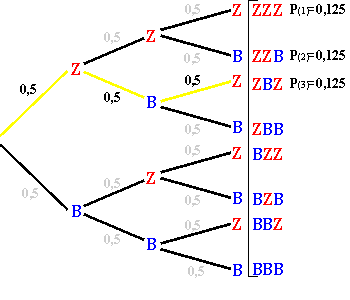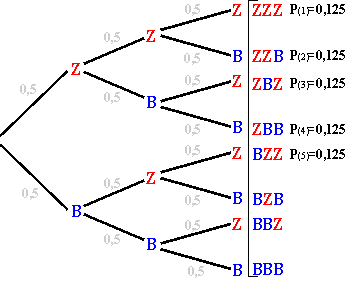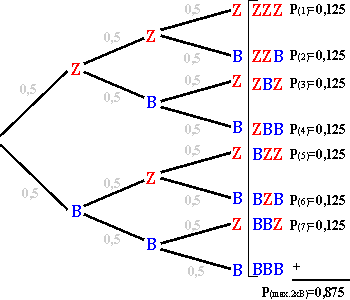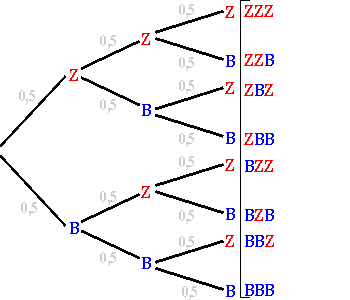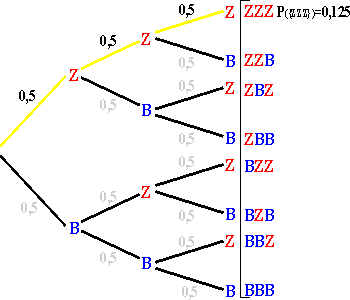
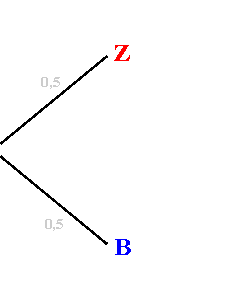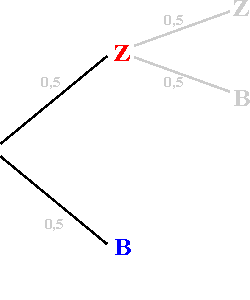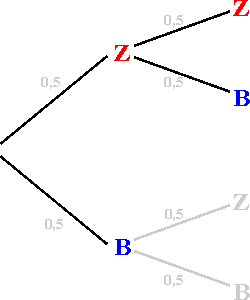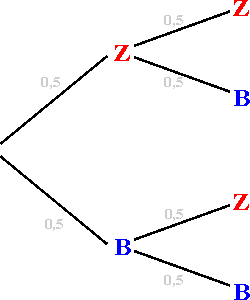
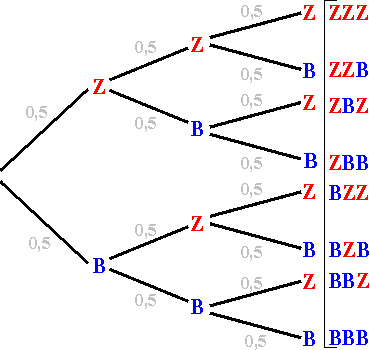
| Wollen wir nun beispielsweise die Wahrscheinlichkeit dafür errechnen,
dass das Ereignis  eintritt, so müssen wir
vom Anfang bis zum Ende dem Pfad folgen, aus dem das gewünschte Ergebnis
hervorgeht und die Einzelwahrscheinlichkeiten entlang dieses Pfades multiplizieren. eintritt, so müssen wir
vom Anfang bis zum Ende dem Pfad folgen, aus dem das gewünschte Ergebnis
hervorgeht und die Einzelwahrscheinlichkeiten entlang dieses Pfades multiplizieren.
d.h.: 0,5 x 0,5 x 0,5 = 0,125
=>Die Wahrscheinlichkeit, für dieses Ereignis beträgt also 12,5%
| 1. Pfadregel: Die Wahrscheinlichkeit, dass
ein bestimmtes Elementarereignis eintritt, wird dadurch errechnet, dass die
Einzelwahrscheinlichkeiten
entlang eines Pfades miteinander multipliziert werden.
| |

 B(aum)
B(aum)
 (ahl) oder
(ahl) oder
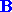 (aum) eintreten.
(aum) eintreten.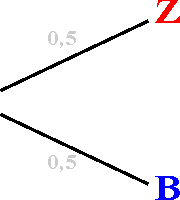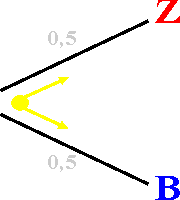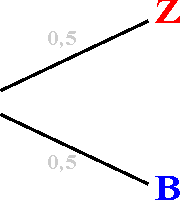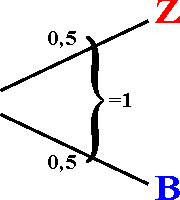

 eintritt, so müssen wir
vom Anfang bis zum Ende dem Pfad folgen, aus dem das gewünschte Ergebnis
hervorgeht und die Einzelwahrscheinlichkeiten entlang dieses Pfades multiplizieren.
eintritt, so müssen wir
vom Anfang bis zum Ende dem Pfad folgen, aus dem das gewünschte Ergebnis
hervorgeht und die Einzelwahrscheinlichkeiten entlang dieses Pfades multiplizieren.