Arbeitsblatt zum Aufstellen von Funktionsgleichungen

Allgemein

Begriffserklärung

• Was versteht man unter dem Aufstellen von Funktionsgleichungen?
• Wie bestimmt man Extremstellen (HP/TP)?
• Wie bestimmt man Wendestellen?

Erstes Beispiel

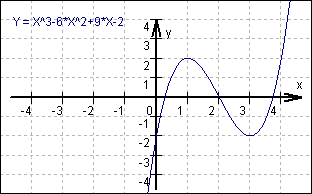
Gesucht ist eine ganzrationale Funktion 3. Grades, deren Graph die y-Achse bei -2 schneidet, bei x = 3 einen Tiefpunkt (TP) und in W(2/0) einen Wendepunkt (WP) hat.

a) Voraussetzungen

Aufstellen der allgemeinen Polynomfunktiongleichung für den jeweiligen Grad der gesuchten Funktion.

In unserem Fall also f (x) = ax³ + bx² + cx + d

Danach werden von dieser Polynomfunktion die Ableitungen f ' und f '' gebildet.

f    (x) =   ax³   + bx² + cx + d
f '  (x) = 3ax²  + 2bx + c
f '' (x) = 6ax   + 2b

Übersetzungshilfe:

P(x_p/y_p)  G_f   f (x_p) = y_p

Steigung m	bei x = x0		f '  (x0) = m
Extrema	bei x = x0		f '  (x0) = 0
Wendepunkt	bei x = x0		f '' (x0) = 0
Terrassenpunkt	bei x = x0		f '  (x0) = 0 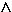   f '' (x0) = 0

aus dem Text folgt :

"schneidet die y-Achse bei -2"

Was folgern Sie aus dieser Aussage?

"x = 3 ist eine Extremstelle"

In welche Ableitung der Funktion muss x = 3 eingesetzt werden, um die Bedingungsgleichung zu erhalten?

" W(2/0) einen Wendepunkt" bedeutet? 

b) Lösung

Aus diesen Erkenntnissen werden Bedingungsgleichungen aufgestellt:

aus P(0/-2) 

  f(0) = -2   -2 = a0³ + b0² + c0 + d

 d = -2

(1) Extrema bei x = 3

f '(3) = 0 0 = 3a3² + 2b3 + c

0 = 27a + 6b + c

(2) Wendepunkt WP (2/0)

f ''(2) = 0 0 = 6a2 + 2b

0 = 12a + 2b

(3) aus WP(2/0)

f(2) = 0 0 = a2³ + b2² + c2 + d

0 = 8a + 4b + 2c - 2

Die drei Bedinungsgleichungen mit drei Unbekannten sind nun mittels Additionsverfahren zu lösen:

      0 = 27a + 6b + c (1)
(-)  1 =   4a + 2b + c (3) zuvor durch 2 dividiert und +1 addiert

a = 1 in (2) eingesetzt:

  0  =  12 + 2b    |-2b
12  =  -2b
b    =  -6

a = 1 und b = -6 in (1) eingesetzt:

0 = 27 - 36 + c
0 = -9 + c
c = 9

Was machen Sie mit den so erhaltenen Konstanten?

f (x) = ax³ + bx² + cx + d

einsetzen von a = 1, b = -6, c = 9 und d = -2 ergibt:

f (x) = x³ - 6x² + 9x - 2

Zusammenfassung:

1. Den Funktionsterm mit variablen Koeffizienten ansetzen

2. Die Bedingungen in Gleichungen übersetzen

3. Das Gleichungssystem lösen

Zweites Beispiel

Gesucht ist eine Polynomfunktion 3.Grades mit folgenden Eigenschaften:

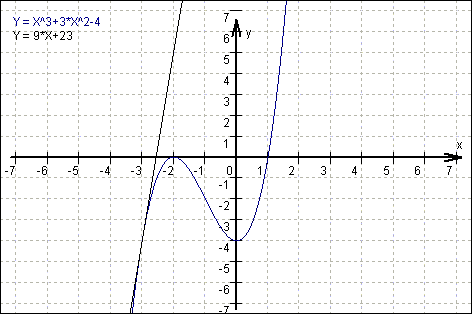
P(-2/0) sei ein Hochpunkt, die Tangente im Punkt Q(-3/q) habe die Steigung 9, W(-1/w) sei ein Wendepunkt.

(3) - (2) (5)

in (4):

0 = -6 + 2b b = 3

in (2):

0 = 12 - 12 + c c = 0

in (1):

0 = -8 + 12 + d d = -4

Damit ergibt sich die einzige Funktion, welche diese Bedingungen erfüllt:

f (x) = x³ + 3x² -4

Ergänzung

Mit den nun in Form von Fragen dargebotenen möglichen Formulierungen soll ein kleiner Überblick über diese erfolgen.

Überlegen sie sich für die jeweiligen Bedingungungen an die Funktion f (x) = ax³ + bx² + cx + d eine Gleichung für die Unbekannten.

• Der Punkt mit den Koordinaten (2/5) liegt auf  f ?
• f  hat an der Stelle x = - 2 die Steigung 3?
• Der Punkt mit den Koordinaten (-1/4) ist ein Hochpunkt (Tiefpunkt)?
• (5/-2) ist ein Wendepunkt von  f ?
• f  hat an der Stelle x = - 4 eine zur Geraden y = 15x - 3 parallele Tangente?
• f  hat an der Stelle x = -3 die Tangente y = 9x - 7 ?
• f  hat an den Stellen x = -3 und x = 6 parallele Tangenten ? 
• f  hat an der Stelle x = -1 eine waagrechte Tangente? 
• f  berührt die Funktion g (x) = 1 -  an der Stelle x = 2 ( Dazu muss erst noch die Ableitung von g mit g´ (x) = berechnet werden)?
• f  hat an der Stelle x = 7 die Wendetangente y = -3x + 5 ?
• f  berührt die x-Achse im Ursprung (die x-Achse hat die Steigung 0) ?
• f  hat an der Stelle x = 1 die Normale y = 2x + 3 ?
• f  hat an der Stelle x = 4 eine zur Geraden y = -3x + 4 senkrechte Tangente?
• f  hat an der Stelle x = 4 eine zur Geraden y = -3x + 4 parallele Normale?

Aufgaben zum Aufstellen von Funktionsgleichungen