Übungsblatt zum Aufstellen von Funktionsgleichungen

Alle Lösungen auf einem Blatt: hier klicken!

1. Funktion 3. Grades : f (x) = ax³ + bx² + cx + d
WP im Ursprung, Extrempunkt E (-1/4)

2. f (x) = ax³ + bx² + cx + d
Kurve berührt die x-Achse im Ursprung und schneidet
sie im Punkt P (-6/0) mit dem Anstieg

3. Die Funktion f mit f (x) = ax³ + bx² + cx + d hat dieselben Nullstellen wie
die Funktion g mit g (x) = 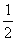x³ - 2x. Die beiden zugehörigen Tangenten im Ursprung O stehen
aufeinander senkrecht. Bestimmen Sie die Koeffizienten a, b, c und d.

4. Der Graf einer Poynomfunktion 3. Grades geht durch den Ursprung O.
Die Tangente im Wendepunkt W (2/1) hat die Steigung -1,5.
Stellen Sie die Funktionsleichung auf.

5. Eine ganzrationale Funktion 3. Grades hat im Ursprung einen Wendepunkt,
weiterhin in P (-2/2) eine waagrechte Tangente.

6. Der Graf einer Polynomfunktion 3. Grades hat in A (2/3) die Steigung -9 ,
bei x = -1 einen Extremstelle und auf der y-Achse einen Wendepunkt.

7. Welche Polynomfunktion 3. Grades erfüllt folgende Bedingungen:
Der Ursprung liegt auf der Kurve, W (2/1) ist ein Terrassenpunkt.

8. Der Graf einer Polynomfunktion 3. Grades hat im Punkt P₁ (2/?) einen Wendepunkt
mit der Tangente 3x + y = 6. Außerdem geht er durch P₂ (0/-2)

9. Der Graf einer ganzrationalen Funktion 4. Grades ist symmetrisch zur y-Achse
Er hat im Punkt P₁ (2/0) die Steigung 2 und im Punkt P₂ (-1/y₂) einen
Wendepunkt. Wie lautet die Funktionsgleichung?

10. Die Grafen einer Funktionenschar 4. Grades f_a haben folgende Eigenschaften:
Sie sind achsensymmetrisch, gehen durch P (0/2) und haben an der Stelle
x = 1 die Steigung 12.

(Druckdatei erstellen)